Skip to main content
Springer Nature Link
Log in

Super \(K_{1,p}\)-Connectivity of Locally Twisted Cubes

  • Conference paper
  • First Online:
Innovative Mobile and Internet Services in Ubiquitous Computing (IMIS 2022)

Part of the book series: Lecture Notes in Networks and Systems ((LNNS,volume 496))

  • 608 Accesses

Abstract

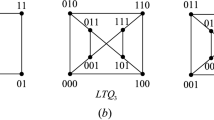
Interconnection networks are emerging as an approach to solving system-level communication problems. A network is abstractly modeled by a graph. For \(p \ge 1\), a p-star \(K_{1,p}\) includes \(p+1\) nodes such that a single node (called center) is linked to each of the other p nodes. The connectivity has long been a classic factor that characterizes both network reliability and fault tolerance. A set F of node subsets of G is a \(K_{1,p}\)-cut if \(G-F\) is disconnected, and each element of F happens to induce a p-star in G. A super \(K_{1,p}\)-cut F of G is a \(K_{1,p}\)-cut in G such that the smallest component of \(G-F\) contains two or more nodes. Then the super \(K_{1,p}\)-connectivity of G, denoted by \(\kappa '(G|K_{1,p})\), is the cardinality of the minimum super \(K_{1,p}\)-cut of G. The locally twisted cube \(LTQ_n\) is a promising alternative to the hypercube and can serve as the backbone architecture of high-performance computing. In this article, we are inspired to determine \(\kappa '(LTQ_n|K_{1,p})\) for \(p=1,2,3\).

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Akers, S.B., Krishnamurthy, B.: A group theoretic model for symmetric interconnection networks. IEEE Trans. Comput. 38(4), 555–566 (1989)

    Google Scholar 

  2. Bondy, J.A., Murty, U.S.R.: Graph Theory. Springer, London (2008)

    Book  Google Scholar 

  3. Chang, N.W., Hsieh, S.Y.: \(\{2,3\}\)-extraconnectivities of hypercube-like networks. J. Comput. Syst. Sci. 79, 669–688 (2013)

    Article  MathSciNet  Google Scholar 

  4. Dally, W.J., Towles, B.: Principles and Practices of Interconnection Networks. Morgan Kaufmann, San Francisco (2004)

    Google Scholar 

  5. Day, K., Tripathi, A.: Arrangement graphs: a class of generalized star graphs. Inf. Process. Lett. 42(5), 235–241 (1992)

    Article  MathSciNet  Google Scholar 

  6. Efe, K.: The crossed cube architecture for parallel computing. IEEE Trans. Parallel Distrib. Syst. 3, 513–524 (1992)

    Article  Google Scholar 

  7. Fábrega, J., Fiol, M.A.: On the extraconnectivity of graphs. Discret. Math. 155, 49–57 (1996)

    Article  MathSciNet  Google Scholar 

  8. Flahive, M., Bose, B.: The topology of gaussian and Eisenstein-Jacobi interconnection networks. IEEE Trans. Parallel Distrib. Syst. 21(8), 1132–1142 (2010)

    Article  Google Scholar 

  9. Han, Y., Fan, J., Zhang, S., Yang, J., Qian, P.: Embedding meshes into locally twisted cubes. Inf. Sci. 180, 3794–3805 (2010)

    Article  MathSciNet  Google Scholar 

  10. Harary, F., Hayes, J.P., Wu, H.J.: A survey of the theory of hypercube graphs. Comput. Math. Appl. 15, 277–289 (1988)

    Article  MathSciNet  Google Scholar 

  11. Hsieh, S.Y., Tu, C.J.: Constructing edge-disjoint spanning trees in locally twisted cubes. Theor. Comput. Sci. 410, 926–932 (2009)

    Article  MathSciNet  Google Scholar 

  12. Hsieh, S.Y., Wu, C.Y.: Edge-fault-tolerant hamiltonicity of locally twisted cubes under conditional edge faults. J. Comb. Optim. 19, 16–30 (2010)

    Article  MathSciNet  Google Scholar 

  13. Hsu, L.H., Lin, C.K.: Graph Theory and Interconnection Networks. CRC Press, New York (2008)

    Book  Google Scholar 

  14. Hung, R.W.: Embedding two edge-disjoint Hamiltonian cycles into locally twisted cubes. Theor. Comput. Sci. 412, 4747–4753 (2011)

    Article  MathSciNet  Google Scholar 

  15. Kung, T.L.: Flexible cycle embedding in the locally twisted cube with nodes positioned at any prescribed distance. Inf. Sci. 242, 92–102 (2013)

    Article  MathSciNet  Google Scholar 

  16. Kung, T.L., Chen, H.C.: Improving the panconnectedness property of locally twisted cubes. Int. J. Comput. Math. 91(9), 1863–1873 (2014)

    Article  MathSciNet  Google Scholar 

  17. Kung, T.L., Chen, H.C., Lin, C.H., Hsu, L.H.: Three types of two-disjoint-cycle-cover pancyclicity and their applications to cycle embedding in locally twisted cubes. Comput. J. 64(1), 27–37 (2021)

    Article  MathSciNet  Google Scholar 

  18. Kung, T.L., Lin, C.K.: Cluster connectivity of hypercube-based networks under the super fault-tolerance condition. Discret. Appl. Math. 293, 143–156 (2021)

    Article  MathSciNet  Google Scholar 

  19. Kung, T.L., Teng, Y.H., Lin, C.K.: Super fault-tolerance assessment of locally twisted cubes based on the structure connectivity. Theor. Comput. Sci. 889, 25–40 (2021)

    Article  MathSciNet  Google Scholar 

  20. Leighton, F.T.: Introduction to Parallel Algorithms and Architectures: Arrays \(\cdot \) Trees \(\cdot \) Hypercubes. Morgan Kaufmann, San Mateo (1992)

    MATH  Google Scholar 

  21. Li, T.K., Lai, C.J., Tsai, C.H.: A novel algorithm to embed a multi-dimensional torus into a locally twisted cube. Theor. Comput. Sci. 412, 2418–2424 (2011)

    Article  MathSciNet  Google Scholar 

  22. Loh, P.K.K., Hsu, W., Pan, Y.: The exchanged hypercube. IEEE Trans. Parallel Distrib. Syst. 16(9), 866–874 (2005)

    Article  Google Scholar 

  23. Ma, M., Xu, J.M.: Panconnectivity of locally twisted cubes. Appl. Math. Lett. 19, 673–677 (2006)

    Article  MathSciNet  Google Scholar 

  24. Ma, M., Xu, J.M.: Weak edge-pancyclicity of locally twisted cubes. ARS Comb. 89, 89–94 (2008)

    MATH  Google Scholar 

  25. Martínez, C., Beivide, R., Stafford, E., Moretó, M., Gabidulin, E.: Modeling toroidal networks with the gaussian integers. IEEE Trans. Comput. 57(8), 1046–1056 (2008)

    Article  MathSciNet  Google Scholar 

  26. Menger, K.: Zur allgemeinen kurventheorie. Fundam. Math. 10, 96–115 (1927)

    Article  Google Scholar 

  27. Saad, Y., Schultz, M.H.: Topological properties of hypercubes. IEEE Tran. Comput. 37, 867–872 (1988)

    Google Scholar 

  28. Wei, C.C., Hsieh, S.Y.: \(h\)-restricted connectivity of locally twisted cubes. Discret. Appl. Math. 217, 330–339 (2017)

    Article  MathSciNet  Google Scholar 

  29. Xu, X., Zhai, W., Xu, J.M., Deng, A., Yang, Y.: Fault-tolerant edge-pancyclicity of locally twisted cubes. Inf. Sci. 181, 2268–2277 (2011)

    Article  MathSciNet  Google Scholar 

  30. Yang, X., Evans, D.J., Megson, G.M.: The locally twisted cubes. Int. J. Comput. Math. 82, 401–413 (2005)

    Article  MathSciNet  Google Scholar 

  31. Yang, X., Megson, G.M., Evans, D.J.: Locally twisted cubes are 4-pancyclic. Appl. Math. Lett. 17, 919–925 (2004)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work is supported in part by the Ministry of Science and Technology, Taiwan, under Grant No. MOST 109-2221-E-468-009-MY2.

Author information

Authors and Affiliations

  1. Department of Computer Science and Information Engineering, Providence University, Taichung City, Taiwan

    Yuan-Hsiang Teng

  2. Department of Computer Science and Information Engineering, Asia University, Taichung City, Taiwan

    Tzu-Liang Kung

Authors
  1. Yuan-Hsiang Teng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tzu-Liang Kung
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tzu-Liang Kung .

Editor information

Editors and Affiliations

  1. Department of Information and Communication Engineering, Fukuoka Institute of Technology, Fukuoka, Japan

    Leonard Barolli

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Teng, YH., Kung, TL. (2022). Super \(K_{1,p}\)-Connectivity of Locally Twisted Cubes. In: Barolli, L. (eds) Innovative Mobile and Internet Services in Ubiquitous Computing. IMIS 2022. Lecture Notes in Networks and Systems, vol 496. Springer, Cham. https://doi.org/10.1007/978-3-031-08819-3_27

Download citation

Publish with us

Policies and ethics