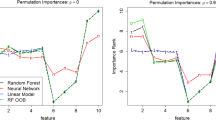
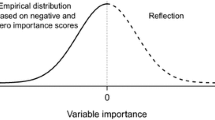
Abstract
Classification and regression trees offer straightforward methods of attributing importance values to input features, either globally or for a single prediction. Conditional feature contributions (CFCs) yield local, case-by-case explanations of a prediction by following the decision path and attributing changes in the expected output of the model to each feature along the path. However, CFCs suffer from a potential bias which depends on the distance from the root of a tree. The by now immensely popular alternative, SHapley Additive exPlanation (SHAP) values appear to mitigate this bias but are computationally much more expensive. Here we contribute a thorough, empirical comparison of the explanations computed by both methods on a set of 164 publicly available classification problems in order to provide data-driven algorithm recommendations to current researchers. For random forests and boosted trees, we find extremely high similarities and correlations of both local and global SHAP values and CFC scores, leading to very similar rankings and interpretations. Unsurprisingly, these insights extend to the fidelity of using global feature importance scores as a proxy for the predictive power associated with each feature.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Synonymous with Saabas value.
- 2.
A python library is available at https://github.com/slundberg/shap.
- 3.
- 4.
The entire experimental design consisted of over 5.5 million ML algorithm and parameter evaluations in total.
- 5.
- 6.
Although a more systematic approach would be to perform statistical tests on the feature scores, see [2], and references therein.
References
Breiman, L.: Random forests. Mach. Learn. 45 (2001). https://doi.org/10.1023/A:1010933404324
Coleman, T., Peng, W., Mentch, L.: Scalable and efficient hypothesis testing with random forests. arXiv preprint arXiv:1904.07830 (2019)
Covert, I., Lundberg, S.M., Lee, S.I.: Understanding global feature contributions with additive importance measures. In: Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H. (eds.) Advances in Neural Information Processing Systems. vol. 33, pp. 17212–17223. Curran Associates, Inc. (2020). https://proceedings.neurips.cc/paper/2020/file/c7bf0b7c1a86d5eb3be2c722cf2cf746-Paper.pdf
Díaz-Uriarte, R., De Andres, S.A.: Gene selection and classification of microarray data using random forest. BMC Bioinform. 7(1), 3 (2006)
Dua, D., Graff, C.: UCI machine learning repository (2017). http://archive.ics.uci.edu/ml
Grömping, U.: Variable importance assessment in regression: linear regression versus random forest. Am. Stat. 63(4), 308–319 (2009)
Kim, H., Loh, W.Y.: Classification trees with unbiased multiway splits. J. Am. Stat. Assoc. 96(454), 589–604 (2001)
Liaw, A., Wiener, M.: Classification and regression by randomforest. R. News 2(3), 18–22 (2002). https://CRAN.R-project.org/doc/Rnews/
Loecher, M.: From unbiased MDI feature importance to explainable AI for trees. arXiv preprint arXiv:2003.12043 (2020)
Loecher, M.: Unbiased variable importance for random forests. Commun. Stat. Theory Methods 51, 1–13 (2020)
Lundberg, S.M., et al.: From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2(1), 56–67 (2020)
Lundberg, S.M., Erion, G.G., Lee, S.I.: Consistent individualized feature attribution for tree ensembles. arXiv preprint arXiv:1802.03888 (2018)
Mentch, L., Zhou, S.: Randomization as regularization: a degrees of freedom explanation for random forest success. J. Mach. Learn. Res. 21(171) (2020)
Menze, B.R., et al.: A comparison of random forest and its GINI importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinform 10(1), 213 (2009)
Olson, R.S., La Cava, W., Mustahsan, Z., Varik, A., Moore, J.H.: Data-driven advice for applying machine learning to bioinformatics problems. arXiv preprint arXiv:1708.05070 (2017)
Patil, I.: Visualizations with statistical details: the ‘ggstatsplot’ approach. J. Open Sour. Softw.6(61), 3167 (2021)
Saabas, A.: Treeinterpreter library (2019). https://github.com/andosa/treeinterpreter
Strobl, C., Boulesteix, A.L., Zeileis, A., Hothorn, T.: Bias in random forest variable importance measures: illustrations, sources and a solution. BMC Bioinform. 8 (2007). https://doi.org/10.1186/1471-2105-8-25
Sun, Q.: tree.interpreter: random forest prediction decomposition and feature importance measure (2020). https://CRAN.R-project.org/package=tree.interpreter, r package version 0.1.1
Sutera, A., Louppe, G., Huynh-Thu, V.A., Wehenkel, L., Geurts, P.: From global to local MDI variable importances for random forests and when they are shapley values. In: Advances in Neural Information Processing Systems, vol. 34 (2021)
Acknowledgements
We thank [15] for providing the complete code (https://github.com/rhiever/sklearn-benchmarks) required both to conduct the algorithm and hyperparameter optimization study, as well as access to the analysis and results. We also thank the authors of [3] for providing us details on their simulations.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 IFIP International Federation for Information Processing
About this paper
Cite this paper
Loecher, M., Lai, D., Qi, W. (2022). Approximation of SHAP Values for Randomized Tree Ensembles. In: Holzinger, A., Kieseberg, P., Tjoa, A.M., Weippl, E. (eds) Machine Learning and Knowledge Extraction. CD-MAKE 2022. Lecture Notes in Computer Science, vol 13480. Springer, Cham. https://doi.org/10.1007/978-3-031-14463-9_2
Download citation
DOI: https://doi.org/10.1007/978-3-031-14463-9_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-14462-2
Online ISBN: 978-3-031-14463-9
eBook Packages: Computer ScienceComputer Science (R0)