Skip to main content
SpringerLink
Log in
SpringerLink
Log in

Explicitly Simple Near-Tie Auctions

  • Conference paper
  • First Online:
Algorithmic Game Theory (SAGT 2022)

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 13584))

Included in the following conference series:

  • 659 Accesses

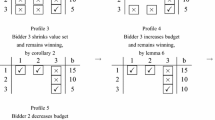
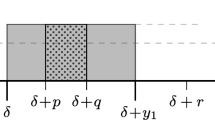
Abstract

We consider the problem of truthfully auctioning a single item, that can be either fractionally or probabilistically divided among several winners when their bids are sufficiently close to a tie.

While Myerson’s Lemma states that any monotone allocation rule can be implemented, truthful payments are computed by integrating over each profile, and may be difficult to comprehend and explain. We look for payment rules that are given explicitly as a simple function of the allocated fraction and the others’ bids. For two agents, this simply coincides with (non-negative) Myerson’s payments. For three agents or more, we characterize the near-tie allocation rules that admit such explicit payments, and provide an iterative algorithm to compute them. In particular we show that any such payment rule must require positive payments to some of the bidders.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 39.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 54.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    For a PSA, \(x_{\underline{k}}\) is a step function. In the general case Myerson’s lemma uses an integral over \(x_{\underline{k}}\) rather than a sum.

  2. 2.

    This can be formally implemented, for example, if each agent j reports (in addition to \(b_j\)) a rational number \(r_j\). In case of a tie, we rank the tied agents according to \(R_j:=r_j\cdot \sqrt{\psi _j}\) where \(\psi _j\) is the j’th prime. Note that \(R_j,R_{j'}\) are never tied (since \(\sqrt{\psi _j}\) are linearly independent over the rationals [1]), unbounded on both sides, and that for any \(r_{j'}<r_{j''}\) and j there is \(r_j\) s.t. \(R_{j'}<R_j<R_{j''}\).

  3. 3.

    We do not allow agents for which \(\alpha _j=0\), as they would change the allocation without being affected.

References

  1. Besicovitch, A.S.: On the linear independence of fractional powers of integers. J. London Math. Soc. 15, 3–6 (1940)

    Article  MathSciNet  Google Scholar 

  2. Cavallo, R.: Optimal decision-making with minimal waste: strategyproof redistribution of VCG payments. In: Proceedings of the Fifth International Joint Conference on Autonomous Agents and Multiagent Systems, pp. 882–889 (2006)

    Google Scholar 

  3. Clark, D.J., Riis, C.: Influence and the discretionary allocation of several prizes. Eur. J. Polit. Econ. 14(4), 605–625 (1998)

    Article  Google Scholar 

  4. Eden, M.: Optimal ties in contests. Technical report, Hebrew University (2006)

    Google Scholar 

  5. Fiat, A., Goldberg, A.V., Hartline, J.D., Karlin, A.R.: Competitive generalized auctions. In: Proceedings of the Thirty-Fourth Annual ACM Symposium on Theory of Computing, pp. 72–81 (2002)

    Google Scholar 

  6. Fischer, S., Güth, W., Kaplan, T.R., Zultan, R.: Auctions with leaks about early bids: analysis and experimental behavior. Econ. Inq. 59(2), 722–739 (2021)

    Article  Google Scholar 

  7. Gama, J.: Functional trees. Mach. Learn. 55(3), 219–250 (2004). https://doi.org/10.1023/B:MACH.0000027782.67192.13

    Article  MATH  Google Scholar 

  8. Graczyk, M., Lasota, T., Trawiński, B.: Comparative analysis of premises valuation models using KEEL, RapidMiner, and WEKA. In: Nguyen, N.T., Kowalczyk, R., Chen, S.-M. (eds.) ICCCI 2009. LNCS (LNAI), vol. 5796, pp. 800–812. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04441-0_70

    Chapter  Google Scholar 

  9. Guo, M., Conitzer, V.: Worst-case optimal redistribution of VCG payments in multi-unit auctions. Games Econ. Behav. 67(1), 69–98 (2009)

    Article  MathSciNet  Google Scholar 

  10. Hashimoto, K.: Strategy-proof rule in probabilistic allocation problem of an indivisible good and money (2015)

    Google Scholar 

  11. Ivanov, D., Nesterov, A.: Identifying bid leakage in procurement auctions: machine learning approach. In: Proceedings of the 2019 ACM Conference on Economics and Computation, pp. 69–70 (2019)

    Google Scholar 

  12. Lee, J.S., Szymanski, B.K.: A novel auction mechanism for selling time-sensitive e-services. In: Seventh IEEE International Conference on E-Commerce Technology (CEC 2005), pp. 75–82. IEEE (2005)

    Google Scholar 

  13. Li, S.: Obviously strategy-proof mechanisms. Am. Econ. Rev. 107(11), 3257–87 (2017)

    Article  Google Scholar 

  14. Ma, H., Meir, R., Parkes, D.C., Zou, J.: Contingent payment mechanisms for resource utilization. In: Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems, pp. 422–430 (2019)

    Google Scholar 

  15. Milgrom, P.: Simplified mechanisms with an application to sponsored-search auctions. Games Econ. Behav. 70(1), 62–70 (2010)

    Article  MathSciNet  Google Scholar 

  16. Morgenstern, J.H., Roughgarden, T.: On the pseudo-dimension of nearly optimal auctions. In: Advances in Neural Information Processing Systems, vol. 28 (2015)

    Google Scholar 

  17. Murillo, J., Muñoz, V., López, B., Busquets, D.: A fair mechanism for recurrent multi-unit auctions. In: Bergmann, R., Lindemann, G., Kirn, S., Pěchouček, M. (eds.) MATES 2008. LNCS (LNAI), vol. 5244, pp. 147–158. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-87805-6_14

    Chapter  Google Scholar 

  18. Myerson, R.B.: Optimal auction design. Math. Oper. Res. 6(1), 58–73 (1981)

    Article  MathSciNet  Google Scholar 

  19. Nedelec, T., El Karoui, N., Perchet, V.: Learning to bid in revenue-maximizing auctions. In: International Conference on Machine Learning, pp. 4781–4789. PMLR (2019)

    Google Scholar 

  20. Núñez, M.: Towards transparent mechanisms. In: Laslier, J.-F., Moulin, H., Sanver, M.R., Zwicker, W.S. (eds.) The Future of Economic Design. SED, pp. 341–346. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-18050-8_47

    Chapter  Google Scholar 

  21. Ohseto, S.: Characterizations of strategy-proof and fair mechanisms for allocating indivisible goods. Econ. Theor. 29(1), 111–121 (2006). https://doi.org/10.1007/s00199-005-0014-1

    Article  MathSciNet  MATH  Google Scholar 

  22. Pápai, S.: Groves sealed bid auctions of heterogeneous objects with fair prices. Soc. Choice Welfare 20(3), 371–385 (2003). https://doi.org/10.1007/s003550200185

    Article  MathSciNet  MATH  Google Scholar 

  23. Quinlan, J.R., et al.: Learning with continuous classes. In: 5th Australian Joint Conference on Artificial Intelligence, vol. 92, pp. 343–348. World Scientific (1992)

    Google Scholar 

  24. Rubinstein, A.: On the computational complexity of optimal simple mechanisms. In: Proceedings of the 2016 ACM Conference on Innovations in Theoretical Computer Science, pp. 21–28 (2016)

    Google Scholar 

  25. Rubinstein, A., Weinberg, S.M.: Simple mechanisms for a subadditive buyer and applications to revenue monotonicity. ACM Trans. Econ. Comput. (TEAC) 6(3–4), 1–25 (2018)

    MathSciNet  Google Scholar 

  26. Varian, H.R.: Position auctions. Int. J. Ind. Organ. 25(6), 1163–1178 (2007)

    Article  Google Scholar 

  27. Yengin, D.: Characterizing welfare-egalitarian mechanisms with solidarity when valuations are private information. BE J. Theor. Econ. 12(1) (2012)

    Google Scholar 

Download references

Acknowledgement

The authors thank Okke Schijvers and Ella Segev for fruitful discussions.

Author information

Authors and Affiliations

  1. Meta, Core Data Science, London, UK

    Reshef Meir & Riccardo Colini-Baldeschi

Authors
  1. Reshef Meir
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Riccardo Colini-Baldeschi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Reshef Meir .

Editor information

Editors and Affiliations

  1. University of Essex, Colchester, UK

    Panagiotis Kanellopoulos

  2. University of Essex, Colchester, UK

    Maria Kyropoulou

  3. University of Essex, Colchester, UK

    Alexandros Voudouris

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Meir, R., Colini-Baldeschi, R. (2022). Explicitly Simple Near-Tie Auctions. In: Kanellopoulos, P., Kyropoulou, M., Voudouris, A. (eds) Algorithmic Game Theory. SAGT 2022. Lecture Notes in Computer Science, vol 13584. Springer, Cham. https://doi.org/10.1007/978-3-031-15714-1_7

Download citation

  • DOI: https://doi.org/10.1007/978-3-031-15714-1_7

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-031-15713-4

  • Online ISBN: 978-3-031-15714-1

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics

Search

Navigation