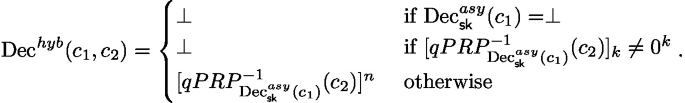Post-quantum Plaintext-Awareness

Abstract

In this paper, we formalize the plaintext-awareness notion in the superposition access model in which a quantum adversary may implement the encryption oracle in a quantum device and make superposition queries to the decryption oracle. Due to various possible ways an adversary can access the decryption oracles, we present six security definitions to capture the plaintext-awareness notion with respect to each way of access. We study the relationships between these definitions and present various implications and non-implications.

Classically, the strongest plaintext-awareness notion (PA2) accompanied by the indistinguishability under chosen-plaintext attack (IND-CPA) notion yields the indistinguishability under chosen-ciphertext attack (IND-CCA) notion. We show that the PA2 notion is not sufficient to show the above relation when targeting the IND-qCCA notion (Boneh-Zhandry definition, Crypto 2013). However, our proposed post-quantum PA2 notion with superposition decryption queries fulfils this implication.

Appendices

A A Preliminaries

1.1 A.1 A.1 Commitment Scheme

In the following, we define a commitment scheme.

Definition 12

(Commitment Scheme). A commitment scheme consists of three polynomial algorithms ${{\,\textrm{Gen}\,}}$, ${{\,\textrm{Com}\,}}$ and ${{\,\textrm{Ver}\,}}$ described below.

• The key generating algorithm ${{\,\textrm{Gen}\,}}$ that on the input of the security parameter $1^n$ returns a public-key $\textsf{pk} _{com}$.

• The commitment algorithm ${{\,\textrm{Com}\,}}$ on the inputs $\textsf{pk} _{com}$ and a message m chooses a randomness r and returns $c:={{\,\textrm{Com}\,}}(\textsf{pk} _{com},m;r)$ and the corresponding opening information $\omega$.

• The verification algorithm ${{\,\textrm{Ver}\,}}$ on the inputs $\textsf{pk} _{com}$, c, $\omega$ and m, either accepts ($b=1$) or rejects ($b=0$).

The scheme has the correctness property, that is, the verification algorithm returns 1 with the probability 1 if $c,\omega$ are the output of ${{\,\textrm{Com}\,}}$:

$$ {{\,\textrm{Pr}\,}}[b=1: \textsf{pk} _{com} \leftarrow {{\,\textrm{Gen}\,}}(1^n), (c,\omega )\leftarrow {{\,\textrm{Com}\,}}(\textsf{pk} _{com},m), b\leftarrow {{\,\textrm{Ver}\,}}(\textsf{pk} _{com},c,\omega ,m)]=1. $$

We define hiding and binding properties of a commitment scheme against a $\textsf{QPT}$ adversary.

Definition 13

We say a commitment scheme $({{\,\textrm{Gen}\,}}(1^n), {{\,\textrm{Com}\,}},{{\,\textrm{Ver}\,}})$ is computationally hiding if for any $\textsf{pk} _{com}\leftarrow {{\,\textrm{Gen}\,}}(1^n)$, for any two messages $m_1,m_2$ and for any $\textsf{QPT}$ distinguisher $\mathcal {D}$

$$\begin{aligned} |{{\,\textrm{Pr}\,}}[\mathcal {D}(\textsf{pk} _{com},c_1)&= 1: (c_1,\omega _1)\leftarrow {{\,\textrm{Com}\,}}_{\textsf{pk} _{com}}(m_1) ]-\\&\!\!{{\,\textrm{Pr}\,}}[\mathcal {D}(\textsf{pk} _{com},c_2) = 1: (c_2,\omega _2)\leftarrow {{\,\textrm{Com}\,}}_{\textsf{pk} _{com}}(m_2) ]| \le \texttt{neg}(n). \end{aligned}$$

Definition 14

A commitment scheme $({{\,\textrm{Gen}\,}}(1^n), {{\,\textrm{Com}\,}},{{\,\textrm{Ver}\,}})$ is computationally binding if for any commitment c, and any $\textsf{QPT}$ adversary $\mathcal {A}$

$$\begin{aligned}&|{{\,\textrm{Pr}\,}}[{{\,\textrm{Ver}\,}}(\textsf{pk} _{com},c,m_1,\omega _1) = 1 \wedge {{\,\textrm{Ver}\,}}(\textsf{pk} _{com},c,m_2,\omega _2) = 1 \wedge m_1\ne m_2: \\ *\qquad \quad \textsf{pk} _{com} \leftarrow {{\,\textrm{Gen}\,}}(1^n), (m_1,\omega _1, m_2,\omega _2)\leftarrow \mathcal {A}(c,\textsf{pk} _{com})]|\le \texttt{neg}(n). \end{aligned}$$

Note that these properties are achievable, for instance, the commitment scheme in [14] fulfills these properties.

1.2 B.2 A.2 Basics of Quantum Computing

Here, we present some basics of quantum information and computation. For two vectors $\mathinner {|{\varPsi }\rangle } = (\psi _1, \psi _2, \cdots , \psi _n)$ and $\mathinner {|{\varPhi }\rangle } = (\phi _1, \phi _2, \cdots , \phi _n)$ in $\mathbb {C}^n$, the inner product is defined as $\langle \,\varPsi ,\varPhi \rangle = \sum _i \psi _i^{*}\phi _i$ where $\psi _i^{*}$ is the complex conjugate of $\psi _i$. Norm of $\mathinner {|{\varPhi }\rangle }$ is defined as $\Vert \mathinner {|{\varPhi }\rangle }\Vert =\sqrt{\langle \,\varPhi ,\varPhi \rangle }$. The n-dimensional Hilbert space $\mathcal {H}$ is the complex vector space $\mathbb {C}^n$ with the inner product defined above. A quantum system is a Hilbert space $\mathcal {H}$ and a quantum state $\mathinner {|{\psi }\rangle }$ is a vector $\mathinner {|{\psi }\rangle }$ in $\mathcal {H}$ with norm 1. A unitary operation over $\mathcal {H}$ is a transformation $\mathbb {U}$ such that $\mathbb {U}\mathbb {U}^{\dag } = \mathbb {U}^{\dag }\mathbb {U}= \mathbb {I}$ where $\mathbb {U}^{\dag }$ is the Hermitian transpose of $\mathbb {U}$ and $\mathbb {I}$ is the identity operator over $\mathcal {H}$. The computational basis for $\mathcal {H}$ consists of $\log n$ vectors $\mathinner {|{b_i}\rangle }$ of length $\log n$ with 1 in the position i and 0 elsewhere. With this basis, the Hadamard unitary is defined as

$$ \mathbb {H}: \mathinner {|{b}\rangle } \rightarrow \frac{1}{\sqrt{2}}(\mathinner {|{\bar{b}}\rangle } + (-1)^{b}\mathinner {|{b}\rangle }), $$

for $b\in \{0,1\}$ where $\bar{b} = 1-b$. An orthogonal projection $\mathbb {P}$ over $\mathcal {H}$ is a linear transformation such that $\mathbb {P}^2 = \mathbb {P} = \mathbb {P}^{\dag }$. A measurement on a Hilbert space is defined with a family of projectors that are pairwise orthogonal. An example of measurement is the computational basis measurement in which any projection is defined by a basis vector. The output of computational measurement on a state $\mathinner {|{\varPsi }\rangle }$ is i with probability $\Vert \langle \,b_i,\varPsi \rangle \Vert ^2$ and the post measurement state is $\mathinner {|{b_i}\rangle }$. For a general measurement $\{\mathbb {P}_i\}_i$, the output of this measurement on a state $\mathinner {|{\varPsi }\rangle }$ is i with probability $\Vert \mathbb {P}_i \mathinner {|{\varPsi }\rangle } \Vert ^2$ and the post measurement state is $\frac{\mathbb {P}_i \mathinner {|{\varPsi }\rangle }}{\Vert \mathbb {P}_i \mathinner {|{\varPsi }\rangle } \Vert }$.

For two quantum systems $\mathcal {H}_1$ and $\mathcal {H}_2$, the composition of them is defined by the tensor product and it is $\mathcal {H}_1 \otimes \mathcal {H}_2$. For two unitary $\mathbb {U}_1$ and $\mathbb {U}_2$ defined over $\mathcal {H}_1$ and $\mathcal {H}_2$ respectively, $(\mathbb {U}_1 \otimes \mathbb {U}_2 )(\mathcal {H}_1 \otimes \mathcal {H}_2) = \mathbb {U}_1 (\mathcal {H}_1) \otimes \mathbb {U}_2(\mathcal {H}_2)$.

B B Discussion on Quantum Eavesdropping

A possible plaintext-awareness definition that considers superposition eavesdropping may be difficult to define due to the no-cloning theorem. For instance, if we follow the above formalism, the plaintext-creator adversary $\mathcal {P}$ upon receiving the input and output registers $Q_{inp}$ and $Q_{out}$ from $\mathcal {A}$, can apply a random unitary to $Q_{inp}$, then applies the encryption unitary and sends both registers back to the adversary. But now it is not clear how one can handle decryption queries. More specifically, the superposition ciphertexts that have been created by calling $\mathcal {P}$ can not be recorded in general and if one of them is submitted as a decryption query, in the real game, the decryption oracle will return the corresponding superposition of messages but in the fake game, $\mathcal {A}^*$ is not able to return the corresponding superposition of messages without access to the internal register of $\mathcal {P}$. Note that if $\mathcal {A}^*$ is able to decrypt those queries without access to the internal register of $\mathcal {P}$ and the secret key, it renders the encryption scheme insecure.

C C Proof of Theorem 8

Proof

Let $\mathcal {X}$ be a $\textsf{QPT}$ adversary that attacks the encryption scheme $\textrm{Enc}$ in the sense of IND-qCCA. We start with IND-qCCA game with the challenge bit $b=0$ ($G_{0}^{qCCA}$) and reach the IND-qCCA game with the challenge bit 1 ($G_{1}^{qCCA}$) by introducing intermediate games that are in a negligible distance.

Let $\mathcal {P}_0$ be a plaintext-creator that upon receiving a query of type $m_0, m_1$ chooses a randomness $r_0$ and returns $\textrm{Enc}(m_0,r_0)$. We replace the challenger in $G_{b=0}^{qCCA}$ with $\mathcal {P}_0$ to reach Game 1.

It is obvious that Game 0 and Game 1 are indistinguishable.

Since $\textrm{Enc}$ is $\textsf{pq} \textsf{PA} 2\text {-}\textsf{Q}_{\textsf{dec}}$ aware there exists a successful ciphertext extractor $\mathcal {A}^*$ for $\mathcal {X}$. Let $\textrm{Q}_{int}$ be the internal register of $\mathcal {X}$. In Game 2, we replace the decryption oracle with $\mathcal {A}^*$.

Since $\mathcal {A}^*$ is a successful ciphertext extractor for $\mathcal {X}$, Game 1 and Game 2 are indistinguishable.

Let $\mathcal {P}_{1}$ be a plaintext-creator algorithm that upon receiving a query of type $m_0,m_1$ chooses randomness $r_1$ and returns $\textrm{Enc}(m_1;r_1)$. We replace $\mathcal {P}_0$ with $\mathcal {P}_1$ in Game 2 to reach Game 3.

Since $\textrm{Enc}$ is IND-qCPA secure, Game 2 and Game 3 are indistinguishable. In more detail, let us assume there is a distinguisher $\mathcal {D}$ with a non-negligible advantage for these two games. Now $\mathcal {Y}=(\mathcal {X}, \mathcal {A}^*, \mathcal {D})$ is an adversary to break IND-qCPA security of $\textrm{Enc}$ that is a contradiction.

In Game 4, we replace $\mathcal {A}^*$ with the decryption oracle.

Since $\mathcal {A}^*$ is a successful plaintext-extractor for $\mathcal {X}$, these two games are indistinguishable.

Finally, we replace $\mathcal {P}_1$ with the challenger in Game 5 to reach $G_{1}^{qCCA}$.

It is clear that Game 4 and Game 5 are indistinguishable. And this finishes the proof.    $\square$

D D Achievability

In this section, we lift a public-key encryption scheme that is PA2 plaintext-aware against a quantum adversary (PA2 notion with classical decryption) to an encryption scheme that is $\textsf{pq} \textsf{PA} 2\text {-}\textsf{Q}_{\textsf{dec}}$.

Let $\varPi ^{asy} = (\textrm{KGen}^{asy}, \textrm{Enc}^{asy}, \textrm{Dec}^{asy})$ be a public-key encryption scheme that is PA2 plaintext-aware. We construct a public-key encryption scheme $\varPi ^{hyb}=(\textrm{KGen}^{hyb}, \textrm{Enc}^{hyb}, \textrm{Dec}^{hyb})$ and shows that it is $\textsf{pq} \textsf{PA} 2\text {-}\textsf{Q}_{\textsf{dec}}$. The encryption scheme $\varPi ^{hyb}$ is defined as :

• The algorithm $\textrm{KGen}^{hyb}$ on input of the security parameter $\eta$ runs $\textrm{KGen}^{asy}(\eta )$ and returns its output $(\textsf{pk},\textsf{sk})$.

• For any message $m\in \{0,1\}^n$, the algorithm $\textrm{Enc}^{hyb}$ chooses a randomness r and returns $\textrm{Enc}_{\textsf{pk}}^{asy}(r)||qPRP_{r}(m||0^{k})$ where qPRP is a strong quantum-secure pseudo-random permutation and k depends on the security parameter $\eta$.

• For any ciphertext $(c_1,c_2)$, $\textrm{Dec}^{hyb}$ first decrypts $c_1$ using $\textsf{sk}$, if the output is $\perp$, it returns $\perp$. Otherwise, it uses the output as the key for qPRP to decrypt $c_2$. If the $k_1$ least significant bits of the outcome is not 0, it returns $\perp$, otherwise it returns the n most significant bits of the outcome.

  

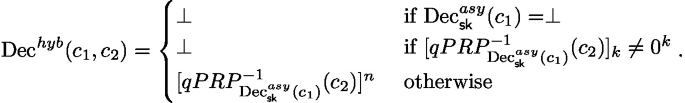
Theorem 9

Under the assumption of the existence of a quantum one-way function, the public-key encryption scheme $\varPi ^{hyb}=(\textrm{KGen}^{hyb}, \textrm{Enc}^{hyb}, \textrm{Dec}^{hyb})$ described above is $\textsf{pq} \textsf{PA} 2\text {-}\textsf{Q}_{\textsf{dec}}$.

Proof

Let $\mathcal {A}$ be an adversary that attacks $\varPi ^{hyb}$ in the sense of $\textsf{pq} \textsf{PA} 2\text {-}\textsf{Q}_{\textsf{dec}}$. We construct an adversary $\mathcal {B}$ that attacks $\varPi ^{asy}$ in the sense of PA2. Let $\mathcal {P}_B$ be a plaintext-creator adversary that upon receiving a query, chooses a randomness r and sends it to the encryption oracle $\varPi ^{asy}$ to receive $\textrm{Enc}^{asy}_{\textsf{pk}}(r)$. Then it sends $\textrm{Enc}^{asy}_{\textsf{pk}}(r)$ to the ciphertex-creator adversary. The adversary $\mathcal {B}$ runs $\mathcal {A}$ and answers to the decryption queries as follows. When $\mathcal {A}$ makes a decryption query $\sum _{c_2}\alpha _{c_2} \mathinner {|{c_1}\rangle }\mathinner {|{c_2}\rangle }$, the adversary $\mathcal {B}$ forwards only the first part of the ciphertext ($c_1$) to its oracle. (Note that $c_1$ is a classical value and it is not entangled with the rest of the query. So forwarding the $c_1$-part does not disturb the decryption query.) If its oracle on input $c_1$ returns $\perp$, $\mathcal {B}$ returns $\perp$. Otherwise, if its oracle on input $c_1$ returns $r\ (\ne \perp )$, $\mathcal {B}$ uses r as the key for qPRP to decrypt the $c_2$-part. Note that if the $k_1$ least significant bits of $qPRP_r^{-1}(c_2)$ is not zero, the output of $\mathcal {B}$ will be $\perp$. Otherwise, the output will be the n most significant bits of $qPRP_r^{-1}(c_2)$. When $\mathcal {A}$ makes a query m to its plaintext-creator $\mathcal {P}_A$, $\mathcal {B}$ makes a query to $\mathcal {P}_B$ to receive the ciphertext $c_1$. Then it sends $(c_1,\pi (m||0^k))$ to $\mathcal {A}$ where $\pi$ is a random permutation. Since $\varPi ^{asy}$ is PA2, there exists a ciphertex extractor $\mathcal {B}^*$ for $\mathcal {B}$.

Now we consider the ciphertex extractor $\mathbb {U}_{\mathcal {A}^*_1}$ where for any $(c_1,c_2)$,

We show that $\mathbb {U}_{\mathcal {A}^*_1}$ is a successful plaintext-extractor for $\mathcal {A}$ in the following.

Game 0: We start with $G_{real}^{\textsf{pq} \textsf{PA} 2\text {-}\textsf{Q}_{\textsf{dec}}}$ that is run by a plaintext-creator $\mathcal {P}_A$ and a distinguisher $\mathcal {D}$.

Game 1: We change the plaintex creator $\mathcal {P}_A$ to a new plaintext-creator $\mathcal {P}'_B$ that upon receiving a query m runs $\mathcal {P}_B$ to obtain $c_1$, then it chooses a random permutation $\pi$ and returns $(c_1,\pi (m||0^k))$. We show that these two games are indistinguishable. An observation is that the first part of the $\mathcal {P}_A$’s output ($c_1$) is independent of $\mathcal {P}_A$ since it is the encryption of a random string that is chosen by the encryption algorithm. In other words, the $c_1$-part is generated exactly the same by $\mathcal {P}_A$ and $\mathcal {P}'_B$. The indistinguishability of the $c_2$-part holds as well since a quantum-secure pseudo-random permutation is indistinguishable from a random permutation.

Game 2: In this game, the decryption queries will be answered by $\mathbb {U}_{\mathcal {A}^*_1}$. An observation is that $\mathcal {A}^*_1$ is indistinguishable from $\textrm{Dec}^{hyb}$ because $\mathcal {B}^*$ is indistinguishable from $\textrm{Dec}^{asy}_{\textsf{sk}}$ (the rest of $\mathcal {A}^*_1$ and $\textrm{Dec}^{hyb}$ are the same). Therefore, these two games remain indistinguishable. In other words, these two games are indistinguishable because $\mathcal {B}^*$ is a successful plaintext-extractor for $\mathcal {B}$.

Game 3: In the last game, we replace the plaintext-creator $\mathcal {P}'_B$ with $\mathcal {P}_A$. The same reasoning as Game 0,1 shows that Game 2 and Game 3 are indistinguishable and this finishes the proof.    $\square$

1.1 C.3 D.1 OAEP transform

The main motivation to present the first definition for plaintext-awareness notion [4] was to show the security of Optimal Asymmetric Encryption Padding (OAEP). Even though our definitions for PA notions are in the standard model, we argue that these definitions apply to the random oracle model as well because queries to the random oracles is a part of the internal register of the adversary. We briefly explain why we think OAEP is $\textsf{pq} \textsf{PA} 1\text {-}\textsf{Q}_{\textsf{dec}}$ plaintext-aware. We take this from a recent work on the IND-qCCA security of OAEP transform [10]. There, Ebrahimi started with the actual decryption algorithm $\mathbb {U}_{\textrm{Dec}}$ and introduced a sequence of indistinguishable decryption algorithms to construct a decryption algorithm $\mathbb {U}_{\textrm{Dec}^{(4)}}$ that does not use the secret key. (Since the queries to the random oracles are quantum, Zhandry’s compressed oracle technique [21] has been used in [10].) This decryption algorithm $\mathbb {U}_{\textrm{Dec}^{(4)}}$ can be invoked by a plaintext-extractor adversary $\mathcal {A}^*$ in the fake game. The indistinguishably of $\mathbb {U}_{\textrm{Dec}}$ and $\mathbb {U}_{\textrm{Dec}^{(4)}}$ gives us the $\textsf{pq} \textsf{PA} 1\text {-}\textsf{Q}_{\textsf{dec}}$ plaintext-awareness. However, whether OAEP is $\textsf{pq} \textsf{PA} 2\text {-}\textsf{Q}_{\textsf{dec}}$ plaintext-aware or not is an open question. The reason is the random oracle queries that are submitted by a plaintext-creator $\mathcal {P}$ are not accessible by $\mathcal {A}^*$. So $\mathbb {U}_{\textrm{Dec}^{(4)}}$ sketched above is not able to decrypt a ciphertext that is obtained by indirect (for instance by a malleability of a ciphertext obtained from $\mathcal {P}$) use of these random oracle queries.