Skip to main content
Springer Nature Link
Log in

Hyperparameter Importance of Quantum Neural Networks Across Small Datasets

  • Conference paper
  • First Online:
Discovery Science (DS 2022)

Part of the book series: Lecture Notes in Computer Science ((LNAI,volume 13601))

Included in the following conference series:

  • 1268 Accesses

Abstract

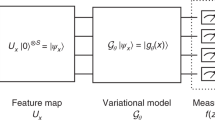
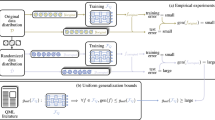
As restricted quantum computers are slowly becoming a reality, the search for meaningful first applications intensifies. In this domain, one of the more investigated approaches is the use of a special type of quantum circuit – a so-called quantum neural network – to serve as a basis for a machine learning model. Roughly speaking, as the name suggests, a quantum neural network can play a similar role to a neural network. However, specifically for applications in machine learning contexts, very little is known about suitable circuit architectures, or model hyperparameters one should use to achieve good learning performance. In this work, we apply the functional ANOVA framework to quantum neural networks to analyze which of the hyperparameters were most influential for their predictive performance. We analyze one of the most typically used quantum neural network architectures. We then apply this to 7 open-source datasets from the OpenML-CC18 classification benchmark whose number of features is small enough to fit on quantum hardware with less than 20 qubits. Three main levels of importance were detected from the ranking of hyperparameters obtained with functional ANOVA. Our experiment both confirmed expected patterns and revealed new insights. For instance, setting well the learning rate is deemed the most critical hyperparameter in terms of marginal contribution on all datasets, whereas the particular choice of entangling gates used is considered the least important except on one dataset. This work introduces new methodologies to study quantum machine learning models and provides new insights toward quantum model selection.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

Notes

  1. 1.

    A 10-fold cross-validation run in our experiment takes on average 262 minutes for 100 epochs with Tensorflow Quantum [7].

References

  1. ANIS, M.S., et al.: Qiskit: an open-source framework for quantum computing (2021). https://doi.org/10.5281/zenodo.2573505

  2. Benedetti, M., Lloyd, E., Sack, S., Fiorentini, M.: Parameterized quantum circuits as machine learning models. Quantum Sci. Technol. 4(4), 043001 (2019)

    Article  Google Scholar 

  3. Bergholm, V., Izaac, J.A., Schuld, M., Gogolin, C., Killoran, N.: Pennylane: Automatic differentiation of hybrid quantum-classical computations. CoRR abs/1811.04968 (2018)

    Google Scholar 

  4. Bischl, B., et al.: OpenML benchmarking suites. In: Proceedings of the Neural Information Processing Systems Track on Datasets and Benchmarks (2021)

    Google Scholar 

  5. Brazdil, P., van Rijn, J.N., Soares, C., Vanschoren, J.: Metalearning: Applications to Automated Machine Learning and Data Mining. Springer, 2nd edn. (2022). https://doi.org/10.1007/978-3-030-67024-5

  6. Breiman, L.: Random forests. Mach. Learn. 45(1), 5–32 (2001)

    Article  MATH  Google Scholar 

  7. Broughton, M., et al.: TensorFlow quantum: a software framework for quantum machine learning. arXiv:2003.02989 (2020)

  8. Caro, M.C., Gil-Fuster, E., Meyer, J.J., Eisert, J., Sweke, R.: Encoding-dependent generalization bounds for parametrized quantum circuits. Quantum 5, 582 (2021)

    Article  Google Scholar 

  9. Eggensperger, K., Hutter, F., Hoos, H.H., Leyton-Brown, K.: Efficient benchmarking of hyperparameter optimizers via surrogates. In: Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, pp. 1114–1120. AAAI Press (2015)

    Google Scholar 

  10. Farhi, E., Goldstone, J., Gutmann, S.: A quantum approximate optimization algorithm. arXiv:1411.4028 (2014)

  11. Feurer, M., Eggensperger, K., Falkner, S., Lindauer, M., Hutter, F.: Auto-Sklearn 2.0: hands-free automl via meta-learning. arXiv:2007.04074v2 [cs.LG] (2021)

  12. Georgescu, I.M., Ashhab, S., Nori, F.: Quantum simulation. Review of modern. Physics 86, 153–185 (2014)

    Google Scholar 

  13. Haug, T., Self, C.N., Kim, M.S.: Large-scale quantum machine learning. CoRR abs/2108.01039 (2021)

    Google Scholar 

  14. Havlíček, V., et al.: Supervised learning with quantum-enhanced feature spaces. Nature 567(7747), 209–212 (2019)

    Article  Google Scholar 

  15. Heimann, D., Hohenfeld, H., Wiebe, F., Kirchner, F.: Quantum deep reinforcement learning for robot navigation tasks. CoRR abs/2202.12180 (2022)

    Google Scholar 

  16. Hutter, F., Hoos, H., Leyton-Brown, K.: An efficient approach for assessing hyperparameter importance. In: Proceedings of the 31th International Conference on Machine Learning, ICML 2014. JMLR Workshop and Conference Proceedings, vol. 32, pp. 1130–1144 (2014)

    Google Scholar 

  17. Jerbi, S., Fiderer, L.J., Nautrup, H.P., Kübler, J.M., Briegel, H.J., Dunjko, V.: Quantum machine learning beyond kernel methods. CoRR abs/2110.13162 (2021)

    Google Scholar 

  18. Jerbi, S., Gyurik, C., Marshall, S., Briegel, H.J., Dunjko, V.: Parametrized quantum policies for reinforcement learning. In: Advances in Neural Information Processing Systems 34, pp. 28362–28375 (2021)

    Google Scholar 

  19. Kandala, A., et al.: Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549(7671), 242–246 (2017)

    Article  Google Scholar 

  20. Kingma, D.P., Ba, J.: Adam: a method for stochastic optimization (2015)

    Google Scholar 

  21. Liu, J.G., Wang, L.: Differentiable learning of quantum circuit born machines. Phys. Rev. A 98, 062324 (2018)

    Article  MathSciNet  Google Scholar 

  22. Liu, Y., Arunachalam, S., Temme, K.: A rigorous and robust quantum speed-up in supervised machine learning. Nat. Phys. 17(9), 1013–1017 (2021)

    Article  Google Scholar 

  23. Marshall, S.C., Gyurik, C., Dunjko, V.: High dimensional quantum machine learning with small quantum computers. CoRR abs/2203.13739 (2022)

    Google Scholar 

  24. Mensa, S., Sahin, E., Tacchino, F., Barkoutsos, P.K., Tavernelli, I.: Quantum machine learning framework for virtual screening in drug discovery: a prospective quantum advantage. CoRR abs/2204.04017 (2022)

    Google Scholar 

  25. Mitarai, K., Negoro, M., Kitagawa, M., Fujii, K.: Quantum circuit learning. Phys. Rev. A 98, 032309 (2018)

    Article  Google Scholar 

  26. Mohr, F., van Rijn, J.N.: Learning curves for decision making in supervised machine learning - a survey. CoRR abs/2201.12150 (2022)

    Google Scholar 

  27. Moll, N., et al.: Quantum optimization using variational algorithms on near-term quantum devices. Quantum Sci. Technol. 3(3), 030503 (2018)

    Article  Google Scholar 

  28. Moussa, C., Calandra, H., Dunjko, V.: To quantum or not to quantum: towards algorithm selection in near-term quantum optimization. Quantum Sci. Technol. 5(4), 044009 (2020)

    Article  Google Scholar 

  29. Moussa, C., Wang, H., Bäck, T., Dunjko, V.: Unsupervised strategies for identifying optimal parameters in quantum approximate optimization algorithm. EPJ Quantum Technol. 9(1) (2022)

    Google Scholar 

  30. Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information: 10th Anniversary. Cambridge University Press, New York (2011)

    MATH  Google Scholar 

  31. Pérez-Salinas, A., Cervera-Lierta, A., Gil-Fuster, E., Latorre, J.I.: Data re-uploading for a universal quantum classifier. Quantum 4, 226 (2020)

    Article  Google Scholar 

  32. Peters, E., et al.: Machine learning of high dimensional data on a noisy quantum processor. NPJ Quantum Inf. 7(1), 161 (2021)

    Article  Google Scholar 

  33. Preskill, J.: Quantum Computing in the NISQ era and beyond. Quantum 2, 79 (2018)

    Article  Google Scholar 

  34. van Rijn, J.N., Hutter, F.: Hyperparameter importance across datasets. In: Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, KDD 2018, pp. 2367–2376. ACM (2018)

    Google Scholar 

  35. Sajjan, M., et al.: Quantum computing enhanced machine learning for physico-chemical applications. CoRR arXiv:2111.00851 (2021)

  36. Saltelli, A., Sobol, I.: Sensitivity analysis for nonlinear mathematical models: numerical experience. Matematicheskoe Modelirovanie 7 (1995)

    Google Scholar 

  37. Sauvage, F., Sim, S., Kunitsa, A.A., Simon, W.A., Mauri, M., Perdomo-Ortiz, A.: Flip: a flexible initializer for arbitrarily-sized parametrized quantum circuits. CoRR abs/2103.08572 (2021)

    Google Scholar 

  38. Schetakis, N., Aghamalyan, D., Boguslavsky, M., Griffin, P.: Binary classifiers for noisy datasets: a comparative study of existing quantum machine learning frameworks and some new approaches. CoRR abs/2111.03372 (2021)

    Google Scholar 

  39. Schuld, M., Killoran, N.: Is quantum advantage the right goal for quantum machine learning? Corr abs/2203.01340 (2022)

    Google Scholar 

  40. Schuld, M., Sweke, R., Meyer, J.J.: Effect of data encoding on the expressive power of variational quantum-machine-learning models. Phys. Rev. A 103, 032430 (2021)

    Article  MathSciNet  Google Scholar 

  41. Sharma, A., van Rijn, J.N., Hutter, F., Müller, A.: Hyperparameter importance for image classification by residual neural networks. In: Kralj Novak, P., Šmuc, T., Džeroski, S. (eds.) DS 2019. LNCS (LNAI), vol. 11828, pp. 112–126. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-33778-0_10

    Chapter  Google Scholar 

  42. Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 41, 303–332 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  43. Sim, S., Johnson, P.D., Aspuru-Guzik, A.: Expressibility and entangling capability of parameterized quantum circuits for hybrid quantum-classical algorithms. Advanced Quantum Technologies 2(12), 1900070 (2019)

    Article  Google Scholar 

  44. Skolik, A., Jerbi, S., Dunjko, V.: Quantum agents in the gym: a variational quantum algorithm for deep q-learning. CoRR abs/2103.15084 (2021)

    Google Scholar 

  45. Sobol, I.M.: Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1(4), 407–414 (1993)

    MathSciNet  MATH  Google Scholar 

  46. Sweke, R., Seifert, J., Hangleiter, D., Eisert, J.: On the quantum versus classical learnability of discrete distributions. Quantum 5, 417 (2021)

    Article  Google Scholar 

  47. Wang, H., Gu, J., Ding, Y., Li, Z., Chong, F.T., Pan, D.Z., Han, S.: QuantumNAT: quantum noise-aware training with noise injection, quantization and normalization. CoRR abs/2110.11331 (2021)

    Google Scholar 

  48. Wang, H., Li, Z., Gu, J., Ding, Y., Pan, D.Z., Han, S.: QOC: quantum on-chip training with parameter shift and gradient pruning. CoRR abs/2202.13239 (2022)

    Google Scholar 

  49. Wossnig, L.: Quantum machine learning for classical data. CoRR abs/2105.03684 (2021)

    Google Scholar 

  50. Zoufal, C., Lucchi, A., Woerner, S.: Quantum generative adversarial networks for learning and loading random distributions. NPJ Quantum Inf. 5(1), 103 (2019)

    Article  Google Scholar 

Download references

Acknowledgements

CM and VD acknowledge support from TotalEnergies. This work was supported by the Dutch Research Council (NWO/OCW), as part of the Quantum Software Consortium programme (project number 024.003.037). This research is also supported by the project NEASQC funded from the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 951821).

Author information

Authors and Affiliations

  1. LIACS, Leiden University, Niels Bohrweg 1, 2333, Leiden, CA, Netherlands

    Charles Moussa, Jan N. van Rijn, Thomas Bäck & Vedran Dunjko

Authors
  1. Charles Moussa
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jan N. van Rijn
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Thomas Bäck
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Vedran Dunjko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Charles Moussa .

Editor information

Editors and Affiliations

  1. University of Montpellier, Montpellier, France

    Poncelet Pascal

  2. INRAE, Montpellier, France

    Dino Ienco

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Moussa, C., van Rijn, J.N., Bäck, T., Dunjko, V. (2022). Hyperparameter Importance of Quantum Neural Networks Across Small Datasets. In: Pascal, P., Ienco, D. (eds) Discovery Science. DS 2022. Lecture Notes in Computer Science(), vol 13601. Springer, Cham. https://doi.org/10.1007/978-3-031-18840-4_3

Download citation

  • DOI: https://doi.org/10.1007/978-3-031-18840-4_3

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-031-18839-8

  • Online ISBN: 978-3-031-18840-4

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics