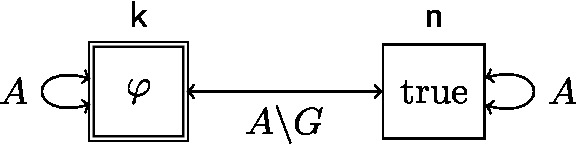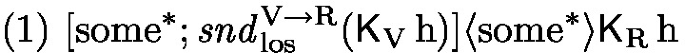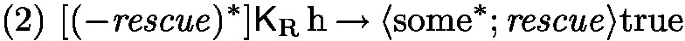Abstract
An ensemble consists of a set of computing entities which collaborate to reach common goals. We introduce epistemic ensembles that use shared knowledge for collaboration between agents. Collaboration is achieved by different kinds of knowledge announcements. For specifying epistemic ensemble behaviours we use formulas of dynamic logic with compound ensemble actions. Our semantics relies on an epistemic notion of ensemble transition systems as behavioural models. These transition systems describe control flow over epistemic states for expressing knowledge-based collaboration of agents. Specifications are implemented by epistemic processes that are composed in parallel to form ensemble realisations. We give a formal operational semantics of these processes that generates an epistemic ensemble transition system. A realisation is correct w. r. t. an ensemble specification if its semantics is a model of the specification.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
An ensemble [13] is formed by a collection of agents which run concurrently to accomplish (together) a certain task. For that purpose agents must collaborate in some way, for instance by explicit interaction via message passing [8, 9]. In the context of the epistemic approach considered here collaboration is based on the knowledge that agents have about themselves, about other agents and about their environment. Any change of knowledge caused by an action of one agent may influence the behaviour of other agents. Hence interaction is implicit. This is related to the ideas of autonomic component ensembles where coordination is achieved via knowledge repositories in which information is stored and from which information is retrieved; see, e.g., [5].
We propose a dynamic logic for specifying properties of epistemic ensembles. Our semantic models are labelled transition systems with atomic ensemble actions as labels. Labelled transitions model two aspects, (i) the control flow of an ensemble and (ii) changes of epistemic information caused by the epistemic effect of an agent action. To model the latter we introduce an epistemic state operator which assigns to each ensemble state s of the system an epistemic state \(\varOmega (s)\) modelling the current epistemic information available in the ensemble. Note that different ensemble states can carry the same epistemic information, in particular if a non-epistemic agent action is performed. Then a transition between the two has a pure control flow effect. The set of ensemble states is restricted to states which are reachable by system transitions from the initial ones. This reflects our intuition that we want to consider ensembles as dynamic processes.
The restriction to reachable states and the ability to model control flow in the semantics is a crucial difference to public announcement logic (PAL) and dynamic epistemic logic (DEL); see, e.g., [6]. Instead of stating requirements for ensemble behaviours these logics are more appropriate for the verification of pre- and postconditions of given epistemic programs. [12] was one of the motivations for our work; it proposes to describe structural properties of ensembles with epistemic logic. An approach which deals with control flow as well are the knowledge-based programs in [7]. The semantic basis are system runs and the interpretation of knowledge tests inside the programs needs a circular procedure by relying on possible system runs at the same time.
After recapitulating basic notions of epistemic logic and epistemic actions in Sect. 2, we present our proposal to specifications of epistemic ensembles in Sect. 3 and provide a (formal) semantics for them in Sect. 4. In Sect. 5 we present an approach to realise epistemic ensemble specifications by a set of concurrently running epistemic processes and we define a correctness notion for such realisations. We finish in Sect. 6 with some concluding remarks.
2 Epistemic Logic and Epistemic Actions
We provide the basis for the epistemic treatment of ensembles considered later on. First, we summarise basic notions of epistemic logic. Then, we provide a summary of epistemic actions and adjust the definitions for their use in epistemic ensemble development. More details can be found in the literature, for instance [3, 6].
2.1 Epistemic Logic
An epistemic signature \(({P}, {A})\) consists of a set \({P}\) of propositions and a finite set \({A}\) of agents. The set \(\varPhi _{{P}, {A}}\) of epistemic formulæ \(\varphi \) over \(({P}, {A})\) is defined by the following grammar:
where \({p}\in {P}\) and \({a}\in {A}\). The epistemic formula \( \textsf{K} _{{a}}\!\mathop {}\varphi \) is to be read as “agent \({a}\) knows \(\varphi \)”. As usual, we write \(\textrm{false}\) for \(\lnot \textrm{true}\), \(\varphi _1 \mathbin {\rightarrow }\varphi _2\) for \(\lnot \varphi _1 \vee \varphi _2\), and \(\varphi _1 \wedge \varphi _2\) for \(\lnot (\lnot \varphi _1 \vee \lnot \varphi _2)\).
For each \({a}\in {A}\), \(\varPhi _{{P}, {A}}^a\) denotes the set of all purely propositional connections (including \(\textrm{true}\) and hence \(\textrm{false}\)) of epistemic formulæ starting with the modality \(\textsf{K}_{{a}}\). These formulæ focus on the knowledge of agent \({a}\). The set \(\varPhi _{{P}, {A}}^a\) is defined by the following grammar:
with \(\varphi \in \varPhi _{{P}, {A}}\). An epistemic structure \(K = (W, R, L)\) over \(({P}, {A})\) consists of a set W of worlds, an \({A}\)-indexed family \(R = (R_a \subseteq W \times W)_{{a}\in {A}}\) of epistemic accessibility relations, and a labelling \(L : W \rightarrow \wp {P}\) which determines for each world \(w \in W\) the set of propositions valid in w. The accessibility relations of epistemic structures are assumed to be equivalence relations. For any \({a}\in {A}\), \((w,w') \in R_{{a}}\) models that agent \({a}\) cannot distinguish the two worlds w and \(w'\).
An epistemic state over \(({P}, {A})\) is a pointed epistemic structure \(\mathfrak {K}= (K, w)\) over \(({P}, {A})\) where \(w \in W\) determines an actual world. The class of all epistemic states over \(({P}, {A})\) is denoted by \( EpiSt({P}, {A}) \).
For any epistemic signature \(({P}, {A})\) and epistemic structure \(K = (W, R, L)\) over \(({P}, {A})\) the satisfaction of an epistemic formula \(\varphi \in \varPhi _{{P}, {A}}\) by K at a point \(w \in W\), written \(K, w \models \varphi \), is inductively defined as follows:
Hence, an agent \({a}\) knows \(\varphi \) at point w if \(\varphi \) holds in all worlds \(w'\) which \({a}\) cannot distinguish from w. For an epistemic state \(\mathfrak {K}= (K,w)\) and for \(\varphi \in \varPhi _{{P}, {A}}\), \(\mathfrak {K}\models \varphi \) means \(K, w \models \varphi \).
Example 1
We consider a (strongly simplified) victim rescue ensemble from a case study [11] of the ASCENS-project [14, 15]. In the ensemble an agent, called \(\textrm{V}\), is a victim who is to be supposed to be rescued by an agent \(\textrm{R}\). There is one atomic proposition \(\textrm{h}\) indicating that the victim needs help and this is true in the actual world. The victim knows this but the rescuer does not. This situation is represented in the following diagram by the epistemic state \((K_0,w_0)\), where, indeed, \(\textrm{R}\) cannot distinguish between the actual world \(w_0\) and the possible world \(w_1\):

The self-loops represent reflexivity of the accessibility relations. Note that \((K_0,w_0) \models \textsf{K} _{\textrm{V}}\!\mathop {}\textrm{h}\) but \((K_0,w_0) \models \lnot \textsf{K} _{\textrm{R}}\!\mathop {}\textrm{h}\) and \((K_0,w_0) \models \lnot \textsf{K} _{\textrm{R}}\!\mathop {} \textsf{K} _{\textrm{V}}\!\mathop {}\textrm{h}.\) \(\square \)
Let \(K_1 = (W_1, R_1, L_1)\), \(K_2 = (W_2, R_2, L_2)\) be two epistemic structures over \(({P}, {A})\). A bisimulation between \(K_1\) and \(K_2\) is a relation \(B \subseteq W_1 \times W_2\) such that for all \((w_1, w_2) \in B\) and all \({a}\in {A}\) the following holds:
-
1.
\(L_1(w_1) = L_2(w_2)\),
-
2.
for each \(w_1' \in W_1\), if \((w_1, w_1') \in R_{1, {a}}\) then there is a \(w_2' \in W_2\) such that \((w_2, w_2') \in R_{2, {a}}\) and \((w_1', w_2') \in B\), and
-
3.
for each \(w_2' \in W_2\), if\((w_2, w_2') \in R_{2, {a}}\) then there is a \(w_1' \in W_1\) such that \((w_1, w_1') \in R_{1, {a}}\) and \((w_1', w_2') \in B\).
Two epistemic states \(\mathfrak {K}_1 = (K_1,w_1)\) and \(\mathfrak {K}_2 = (K_2,w_2)\) over \(({P}, {A})\) are bisimilar, written \(\mathfrak {K}_1 \mathrel {\approx }\mathfrak {K}_2\), if there exists a bisimulation B between \(K_1\) and \(K_2\) such that \((w_1,w_2) \in B\).
The following lemma is a well-known result from epistemic logic; see, e.g., [3, 6].
Lemma 1 (Invariance of epistemic formulæ)
Let \(\mathfrak {K}_1\) and \(\mathfrak {K}_2\) be epistemic states over \(({P}, {A})\) such that \(\mathfrak {K}_1 \mathrel {\approx }\mathfrak {K}_2\). Then, for any \(\varphi \in \varPhi _{{P}, {A}}\), \(\mathfrak {K}_1 \models \varphi \) if, and only if, \(\mathfrak {K}_2 \models \varphi \). \(\square \)
The converse is also valid for image-finite epistemic structures \(K = (W, R, L)\), i.e., if for each world \(w \in W\) and agent \({a}\in {A}\) there exist only finitely many pairs \((w,w') \in R_a\). Note that finiteness of \({A}\) does not imply image finiteness of epistemic structures over \(({P}, {A})\); a counterexample is given in [6, p. 227].
2.2 Epistemic Actions
Epistemic logic deals with static aspects of knowledge captured by epistemic formulæ and their interpretation in epistemic states. A fundamental concept to support dynamic changes of knowledge is public announcement logic (PAL [3]) where knowledge about an epistemic state (formalised by a formula) can be announced to all agents. This may affect the knowledge of the agents leading to a new epistemic situation. More elaborated epistemic actions, like completely private and semi-private announcements, were also considered and a general proposal to model epistemic actions in terms of so-called action models was set up in [2]. In our approach action models will be called action structures in order to avoid confusion with the models of ensemble specifications later on.
An epistemic action structure \(U = (Q, F, pre )\) over \(({P}, {A})\) consists of a set of action points Q, an \({A}\)-indexed family \(F = (F_{{a}} \subseteq Q \times Q)_{{a}\in {A}}\) of epistemic action accessibility relations, and a precondition function \( pre : Q \rightarrow \varPhi _{{P}, {A}}\). We assume again that the accessibility relations are equivalences. In the literature, action points are also called “events”. For any agent \({a}\), \((q,q') \in F_{{a}}\) models that agent \({a}\) cannot distinguish between occurrences of q and \(q'\). For \(q\in Q\), the epistemic formula \( pre (q)\) determines a condition under which q can happen.
An epistemic action over \(({P}, {A})\) is a pointed epistemic action structure \(\mathfrak {u}= (U,q)\) over \(({P}, {A})\) where \(q \in Q\) determines an actual action point. The set \(\mathcal {A}_{{P}, {A}}\) of epistemic actions with (non-deterministic) choice over \(({P}, {A})\) is defined by
where \(\mathfrak {u}= (U,q)\) is an epistemic action over \(({P}, {A})\). The precondition of an epistemic action with choice is given by \( pre (\mathfrak {u}) = pre (q)\), \( pre (\alpha _1 + \alpha _2) = pre (\alpha _1) \vee pre (\alpha _2)\).
Example 2
-
(a)
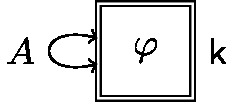
Public announcement of an epistemic formula \(\varphi \in \varPhi _{{P}, {A}}\) to all agents in \({A}\) is modelled by the epistemic action \((U_{ pub ,\varphi },\textsf{k})\) where
$$\begin{aligned} U_{ pub ,\varphi } = (Q_{ pub }, F_{ pub }, pre _{ pub ,\varphi }) \end{aligned}$$with \(Q_{ pub } = \{ \textsf{k} \}\), \(F_{ pub , {a}} = \{ (\textsf{k}, \textsf{k}) \}\) for all \({a}\in {A}\), and \( pre _{ pub ,\varphi } = \{ \textsf{k} \mapsto \varphi \}.\) There is only one action point \(\textsf{k}\) and hence any agent in \({A}\) considers only the occurrence of \(\textsf{k}\) possible. According to the precondition of \(\textsf{k}\) the action can only be executed in an epistemic state \(\mathfrak {K}\) where the announced formula \(\varphi \) holds. The epistemic action \((U_{ pub ,\varphi },\textsf{k})\) is graphically represented by the following diagram.
-
(b)
Private announcement of an epistemic formula \(\varphi \in \varPhi _{{P}, {A}}\) to a group \(G \subseteq {A}\) of agents is modelled by the epistemic action \((U_{ priv ,G,\varphi },\textsf{k})\) graphically represented by the following diagram:
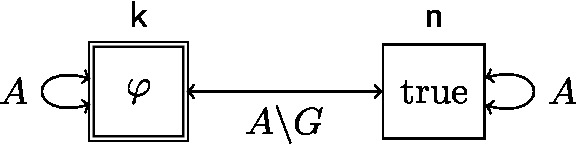
The action structure \(U_{ priv ,G,\varphi }\) has two action points \(\textsf{k}\) and \(\textsf{n}\). Point \(\textsf{k}\) represents that the announcement of \(\varphi \) happens which should only be the case if \(\varphi \) holds in the current epistemic state and therefore \( pre (\textsf{k}) = \varphi \). Only agents in the group G can recognise this event. All other agents consider it possible that nothing happened which is represented by \(\textsf{n}\). This should not have a proper precondition and therefore \( pre (\textsf{n}) = \textrm{true}\).Footnote 1 \(\square \)
The effect of an epistemic action on an epistemic state is defined by the product update as constructed in [1]. First, we define the product update of an epistemic structure by an epistemic action structure and then we use this for the product update of their pointed versions. The product update of an epistemic structure \(K = (W, R, L)\) over \(({P}, {A})\) and an epistemic action structure \(U = (Q, F, pre )\) over \(({P}, {A})\) is the epistemic structure \(K \lhd U = (W', R', L')\) over \(({P}, {A})\) with
According to the definition of the relations \(R_{{a}}'\) the uncertainty of an agent \({a}\) in a world (w, q) is determined by the uncertainty of \({a}\) about world w and its uncertainty about the occurrence of q. Note that the relations \(R_{{a}}'\) are again equivalence relations and therefore the product update for epistemic structures is well-defined.
Let \(\mathfrak {K}= (K,w) \in EpiSt({P}, {A}) \) be an epistemic state and \(\mathfrak {u}= (U,q)\) be an epistemic action over \(({P}, {A})\). If \(\mathfrak {K}\models pre (\mathfrak {u})\) then the product update of \(\mathfrak {K}\) and \(\mathfrak {u}\) is defined and given by the epistemic state \(\mathfrak {K}\lhd \mathfrak {u}= (K \lhd U, (w,q)) \in EpiSt({P}, {A}) \).
The semantics of each epistemic action with choice \(\alpha \in \mathcal {A}_{{P}, {A}}\) is given by a set of relations \(\llbracket \alpha \rrbracket \subseteq EpiSt({P}, {A}) \times EpiSt({P}, {A}) \) between epistemic states inductively defined by:
Note that for each \(\alpha \in \mathcal {A}_{{P}, {A}}\) and \(\mathfrak {K}\in EpiSt({P}, {A}) \) it holds: There exists a \(\mathfrak {K}' \in EpiSt({P}, {A}) \) such that \((\mathfrak {K}, \mathfrak {K}') \in \llbracket \alpha \rrbracket \) if, and only if, \(\mathfrak {K}\models pre (\alpha )\).
Example 3
We consider the victim rescue example from Example 1 and instantiate private announcement of Example 2(b) to the case in which it is privately announced to \(\textrm{R}\) that \(\textrm{V}\) knows that \(\textrm{h}\) holds. Thus we consider the epistemic action \((U_{ priv ,\{\textrm{R}\}, \textsf{K} _{\textrm{V}}\!\mathop {}\textrm{h}},\textsf{k})\) represented by the following diagram where \(\textrm{V}\) does not know whether \(\textrm{R}\) got an announcement:

We apply this action to the epistemic state \((K_0,w_0)\) in Example 1. The product update yields the epistemic state \((K_1,(w_0,\textsf{k}))\) shown, without reflexive accessibility edges, below. The world \((w_1,\textsf{k})\) does not appear since \((K_0,w_1) \not \models \textsf{K} _{\textrm{V}}\!\mathop {}\textrm{h}\) which is the precondition of \(\textsf{k}\).

Note that \((K_1,(w_0,\textsf{k})) \models \textsf{K} _{\textrm{R}}\!\mathop {} \textsf{K} _{\textrm{V}}\!\mathop {}\textrm{h}\) but \((K_1,(w_0,\textsf{k})) \models \lnot \textsf{K} _{\textrm{V}}\!\mathop {} \textsf{K} _{\textrm{R}}\!\mathop {} \textsf{K} _{\textrm{V}}\!\mathop {}\textrm{h}\), i.e. \(\textrm{R}\) knows that \(\textrm{V}\) knows that h holds, but \(\textrm{V}\) does not know that \(\textrm{R}\) knows this.
If we apply the epistemic action \((U_{ priv ,\{\textrm{R}\}, \textsf{K} _{\textrm{V}}\!\mathop {}\textrm{h}},\textsf{n})\) to \((K_0,w_0)\) we obtain the epistemic state \((K_1,(w_0,\textsf{n}))\). Note that \((K_1,(w_0,\textsf{n})) \models \lnot \textsf{K} _{\textrm{R}}\!\mathop {} \textsf{K} _{\textrm{V}}\!\mathop {}\textrm{h}\). \(\square \)
The next lemma shows that bisimulation is preserved by application of epistemic actions; see, e.g., [6].
Lemma 2
Let \(\mathfrak {K}_1\) and \(\mathfrak {K}_2\) be epistemic states over \(({P}, {A})\) such that \(\mathfrak {K}_1 \mathrel {\approx }\mathfrak {K}_2\) and let \(\mathfrak {u}\) be an epistemic action over \(({P}, {A})\). Then \(\mathfrak {K}_1 \lhd \mathfrak {u}\) is defined, if and only if, \(\mathfrak {K}_2 \lhd \mathfrak {u}\) is defined and then it holds \(\mathfrak {K}_1 \lhd \mathfrak {u}\mathrel {\approx }\mathfrak {K}_2 \lhd \mathfrak {u}\). \(\square \)
We generalise Lemma 2 to epistemic actions with choice. The proof is straightforward by induction on the form of \(\alpha \).
Lemma 3
Let \(\mathfrak {K}_1\) and \(\mathfrak {K}_2\) be as in Lemma 2 such that \(\mathfrak {K}_1 \mathrel {\approx }\mathfrak {K}_2\) and let \(\alpha \) be an epistemic action with choice. Then, for any \(\mathfrak {K}_1'\) with \((\mathfrak {K}_1,\mathfrak {K}_1') \in \llbracket \alpha \rrbracket \), there exists \(\mathfrak {K}_2'\) with \((\mathfrak {K}_2,\mathfrak {K}_2') \in \llbracket \alpha \rrbracket \) such that \(\mathfrak {K}_1' \mathrel {\approx }\mathfrak {K}_2'\); the converse holds for any \(\mathfrak {K}_2'\) with \((\mathfrak {K}_2,\mathfrak {K}_2') \in \llbracket \alpha \rrbracket \).
\(\square \)
3 Epistemic Ensemble Specifications
An ensemble is formed by a collection of agents which run concurrently to accomplish (together) a certain task. For that purpose agents must collaborate in some way, for instance by explicit interaction via message passing [8, 9]. In the context of the epistemic approach considered here collaboration is based on the knowledge that agents have about themselves, about other agents and about their environment. Any change of knowledge caused by an action of one agent may influence the behaviour of other agents. Hence interaction is implicit.
Formally, an agent action is given by an action name e to which an agent o(e) is associated, the “owner” of e, who is able to execute that action. An epistemic ensemble signature \( \varSigma = ({P}, {A}, E )\) consists of an epistemic signature \(({P}, {A})\) and a set \( E \) of agent actions such that for each \(e \in E , o(e) \in {A}\). The set \( E \) is split into a set \( eE \) of epistemic agent actions and a set \( nE \) of non-epistemic agent actions. The idea is that any agent action may have an effect on the control flow of an ensemble. The non-epistemic agent actions, however, do not change the epistemic state of an ensemble while epistemic agent actions in general do.
The epistemic effect of an agent action \(e \in E \) is formalised by a relation \( eeff (e) \subseteq EpiSt({P}, {A}) \times EpiSt({P}, {A}) \) between epistemic states over \(({P}, {A})\). For non-epistemic agent actions \(e \in nE \) we define \( eeff (e) = \{(\mathfrak {K},\mathfrak {K}) \mid \mathfrak {K}\in EpiSt({P}, {A}) \}\). The non-epistemic agent actions are specific actions depending on the application at hand. For epistemic agent actions \(e \in eE \) their epistemic effect must be explicitly defined. For this purpose we associate to e an epistemic action expression with choice \(\alpha \in \mathcal {A}_{{P}, {A}}\), whose semantics is clear from Sect. 2.2, and thus define \( eeff (e) = \llbracket \alpha \rrbracket \). Moreover, we set \( pre (e) = pre (\alpha )\) and require that \( pre (e) \in \varPhi _{{P}, {A}}^{o(e)}\). This constraint expresses that an epistemic agent action with owner \({a}\) should have a precondition which concerns, and hence can be tested, by \({a}\); similarly to the knowledge tests of knowledge-based programs in [7]. Thus the epistemic action expressions in Sect. 2.2. will be used as primitives to define the epistemic effect of higher level epistemic actions for agents.
In this paper we assume given, for each epistemic signature \(({P}, {A})\), the following set of epistemic agent actions from which particular instantiations can be chosen for a concrete ensemble signature.
Public Announcement By an Agent: This action is a special case of public announcement such that the announcement is performed by an agent \({a}\) “inside” the system. As a consequence, agent \({a}\) does not simply announce a formula \(\varphi \) but it must indeed know \(\varphi \) and must announce that, i.e. \( \textsf{K} _{{a}}\!\mathop {}\varphi \). Formally, for each \({a}\in {A}\) and \(\varphi \in \varPhi _{{P}, {A}}\), public announcement by \({a}\) is denoted by the epistemic agent action \( pub ^{{a}}( \textsf{K} _{{a}}\!\mathop {}\varphi )\) over \(({P}, {A})\) with owner \(o( pub ^{{a}}( \textsf{K} _{{a}}\!\mathop {}\varphi )) = {a}\). The epistemic effect of this action is defined by \( eeff ( pub ^{{a}}( \textsf{K} _{{a}}\!\mathop {}\varphi )) =_{\textrm{def}} \llbracket (U_{ pub , \textsf{K} _{{a}}\!\mathop {}\varphi },\textsf{k})\rrbracket \) where the latter is the epistemic public announcement action in Example 2(a) with semantics defined by product update as described in Sect. 2.2. Note that \( pre ( pub ^{{a}}( \textsf{K} _{{a}}\!\mathop {}\varphi )) = pre (U_{ pub , \textsf{K} _{{a}}\!\mathop {}\varphi }, \textsf{k}) = \textsf{K} _{{a}}\!\mathop {}\varphi \in \varPhi _{{P}, {A}}^{{a}}\).
Reliable Private Sending: In this case there is an agent \(a\) who knows the validity of a formula \(\varphi \) and sends the information that it knows \(\varphi \), i.e. \( \textsf{K} _{a}\!\mathop {}\varphi \), to another agent \(b\). The sending is reliable, i.e. the information will be received by \(b\) and agent \(a\) knows that. Formally, for each \(a, b\in {A}\) and \(\varphi \in \varPhi _{{P}, {A}}\), reliable private sending is denoted by the epistemic agent action \( snd _{\textrm{rel}}^{a\rightarrow b}( \textsf{K} _{a}\!\mathop {}\varphi )\) over \(({P}, {A})\) with owner \(o( snd _{\textrm{rel}}^{a\rightarrow b}( \textsf{K} _{a}\!\mathop {}\varphi )) = a\).
The epistemic effect of this action can be modelled as a special case of private announcement to a group of agents where the group is \(\{ a, b\}\) and the announcement is \( \textsf{K} _{a}\!\mathop {}\varphi \). Hence, we define \( eeff ( snd _{\textrm{rel}}^{a\rightarrow b}( \textsf{K} _{a}\!\mathop {}\varphi )) =_{\textrm{def}} \llbracket (U_{ priv ,\{a,b\}, \textsf{K} _{a}\!\mathop {}\varphi },\textsf{k})\rrbracket \); see Example 2(b). Obviously, \( pre ( snd _{\textrm{rel}}^{a\rightarrow b}( \textsf{K} _{a}\!\mathop {}\varphi )) = \textsf{K} _{a}\!\mathop {}\varphi \in \varPhi _{{P}, {A}}^{a}\) where \(a= o( snd _{\textrm{rel}}^{a\rightarrow b}( \textsf{K} _{a}\!\mathop {}\varphi ))\).
Lossy Private Sending: In this case there is again an agent \(a\) who knows the validity of a formula \(\varphi \) and sends the information \( \textsf{K} _{a}\!\mathop {}\varphi \) to another agent \(b\). But this time the sending is unreliable and the information may get lost. Formally, for each \(a, b\in {A}\) and \(\varphi \in \varPhi _{{P}, {A}}\), lossy private sending is denoted by the epistemic agent action \( snd _{\textrm{los}}^{a\rightarrow b}( \textsf{K} _{a}\!\mathop {}\varphi )\) over \(({P}, {A})\) with owner \(o( snd _{\textrm{los}}^{a\rightarrow b}( \textsf{K} _{a}\!\mathop {}\varphi )) = a\).
For defining the epistemic effect of \( snd _{\textrm{los}}^{a\rightarrow b}( \textsf{K} _{a}\!\mathop {}\varphi )\) we proceed as follows: Let \(U_{ priv ,\{b\}, \textsf{K} _{a}\!\mathop {}\varphi }\) be the epistemic action structure of Example 2(b) instantiated by \(\{ b\}\) and \( \textsf{K} _{a}\!\mathop {}\varphi \). Let \((U_{ priv ,\{b\}, \textsf{K} _{a}\!\mathop {}\varphi }, {\textsf{k}})\) and \((U_{ priv ,\{b\}, \textsf{K} _{a}\!\mathop {}\varphi }), {\textsf{n}})\) be the corresponding epistemic actions. The first action expresses that after \(a\) has sent the information \( \textsf{K} _{a}\!\mathop {}\varphi \), agent \(b\) has received it, but \(a\) (and all other agents) do not know this; they consider it possible that the information did not arrive. The second action expresses that after the sending of \( \textsf{K} _{a}\!\mathop {}\varphi \) by agent \(a\), agent \(b\) has not received anything and \(b\) knows that. Hence, the information is lost, and \(a\) (and all other agents besides \(b\)) do not know whether the information has arrived or not. The effect of lossy private sending must capture both possibilities. Therefore, it is modelled by a non-deterministic choice of the two actions, either the information is received or not. The sender does not know what happened and the receiver knows the sent information if, and only if, it has received it. Formally, we define
Then, \( pre ( snd _{\textrm{los}}^{a\rightarrow b}( \textsf{K} _{a}\!\mathop {}\varphi )) = pre ((U_{ priv ,\{b\}, \textsf{K} _{a}\!\mathop {}\varphi }, {\textsf{k}}) + (U_{ priv ,\{b\}, \textsf{K} _{a}\!\mathop {}\varphi }, {\textsf{n}})) = pre (U_{ priv ,\{b\}, \textsf{K} _{a}\!\mathop {}\varphi }, {\textsf{k}}) \vee pre (U_{ priv ,\{b\}, \textsf{K} _{a}\!\mathop {}\varphi }, {\textsf{n}}) = ( \textsf{K} _{a}\!\mathop {}\varphi \vee \textrm{true}) \in \varPhi _{{P}, {A}}^{a}\).
In the following we assume that \( \varSigma = ({P}, {A}, E )\) is an epistemic ensemble signature. To specify global behaviours of ensembles performed by concurrently running agents we must consider ensemble actions which are formed by various combinations of agent actions. Therefore, the agent actions in \( E \) are considered as atomic ensemble actions while complex ensemble actions are formed by using the standard operators of dynamic logic which are test (\(\varphi ?\)), non-deterministic choice (\(+\)), sequential composition (; ) and iteration (\(^*\)). The set \(\mathcal {E}_{ \varSigma }\) of compound ensemble actions over \( \varSigma \) is defined by the following grammar:
where \( e \in E \) is an agent action and \(\varphi \in \varPhi _{{P}, {A}}\). If \( E \) is finite, we write “\(\textrm{some}\)” for the compound action obtained by combing with “ \(+\) ” all elements of E and, for \(e \in E \), we write \(-e\) for the compound ensemble action obtained by combing with “ \(+\) ” all elements of \(E {\setminus } \{e\}\).
Ensemble formulæ are used to specify properties of ensembles. They extend the formulæ of epistemic logic in Sect. 2.1 by including modalities with (compound) ensemble actions which allow us to specify the dynamic aspects of global ensemble behaviours. The set \(\varPsi _{ \varSigma }\) of epistemic ensemble formulæ over \( \varSigma = ({P}, {A}, E )\) is defined by the following grammar:
where \(\varphi \in \varPhi _{{P}, {A}}\) and \(\pi \in \mathcal {E}_{ \varSigma }\). The formula \(\langle \pi \rangle \psi \) is to be read as “in the current ensemble state it is possible to execute \(\pi \) leading to an ensemble state where formula \(\psi \) holds”. The abbreviations from epistemic logic are extended to epistemic ensemble logic. Furthermore, we abbreviate \(\lnot \langle \pi \rangle \lnot \psi \) by \([\pi ]\psi \) which is to be read as “each execution of \(\pi \) in the current ensemble state leads to an ensemble state where the formula \(\psi \) holds”.
Using the shorthand notations for compound actions for finite \( E \), we can specify safety properties with \([\textrm{some}^*]\psi \); deadlock freeness is expressed by \([\textrm{some}^*]\langle \textrm{some}\rangle \textrm{true}\). Liveness properties like “whenever an action e has happened, an action f can eventually occur”, can be expressed by \([\textrm{some}^*;e]\langle \textrm{some}^*;f\rangle \textrm{true}\). We can also express that an action f must never occur when action e has happened before by \([\textrm{some}^*;e;\textrm{some}^*;f]\textrm{false}\).
Definition 1 (Ensemble specification)
An ensemble specification \( Sp = ( \varSigma , Ax )\) consists of an ensemble signature \( \varSigma \) and a set \( Ax \subseteq \varPsi _{ \varSigma }\) of ensemble formulæ, called axioms of \( Sp \). \(\square \)
Example 4
We provide a requirements specification \( Sp _{ vr } = ( \varSigma _{ vr }, Ax _{ vr })\) for victim rescue ensembles. The epistemic ensemble signature \( \varSigma _{ vr }\) consists of the proposition \(\textrm{h}\), of the two agents \(\textrm{V}\) and \(\textrm{R}\), of the two epistemic agent actions \( snd _{\textrm{los}}^{\textrm{V}\rightarrow \textrm{R}}( \textsf{K} _{\textrm{V}}\!\mathop {}\textrm{h}), snd _{\textrm{rel}}^{\textrm{R}\rightarrow \textrm{V}}( \textsf{K} _{\textrm{R}}\!\mathop {}\textrm{h})\) with owners \(o( snd _{\textrm{los}}^{\textrm{V}\rightarrow \textrm{R}}( \textsf{K} _{\textrm{V}}\!\mathop {}\textrm{h})) = \textrm{V}\) and \(o( snd _{\textrm{rel}}^{\textrm{R}\rightarrow \textrm{V}}( \textsf{K} _{\textrm{R}}\!\mathop {}\textrm{h})) = \textrm{R}\), and two non-epistemic agent actions \( stop , rescue \) with owners \(o( stop ) = \textrm{V}\) and \(o( rescue ) = \textrm{R}\). We use a lossy information transfer from \(\textrm{V}\) to \(\textrm{R}\) since the idea is that the rescuer is moving around in an exploration area and cannot get information when it is outside the victim’s range. The information transfer from \(\textrm{R}\) to \(\textrm{V}\) is reliable, since we assume that once the rescuer is informed it will be close enough to the victim. For a victim rescue ensemble we require the following properties expressed by the two axioms (1) and (2) of \( Ax _{ vr }\):
-
“Whenever the victim performs a lossy sending to the rescuer that it knows that \(\textrm{h}\) is valid, i.e. the victim needs help, it is eventually possible that the rescuer knows this.”
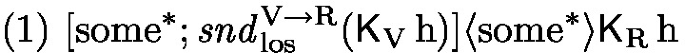
-
“Whenever the rescuer has not yet rescued the victim but knows that the victim needs help, it is eventually possible that the rescuer rescues the victim.”
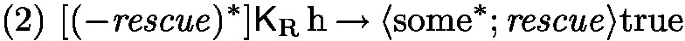
This specification can be generalised in many ways, for instance to more rescuers taking into account that it is sufficient that only one rescuer goes for rescuing. \(\square \)
4 Semantics of Epistemic Ensemble Specifications
We will now turn to the semantics of epistemic ensemble logic and ensemble specifications. Our semantic models are labelled transition systems with atomic ensemble actions (i.e. agent actions) as labels. Labelled transitions model two aspects, (i) the control flow of an ensemble and (ii) changes of epistemic information caused by the epistemic effect of an agent action. To model the latter we introduce an epistemic state operator which assigns to each ensemble state s of the system an epistemic state \(\varOmega (s)\). Ensemble states could be modelled by pairs \(s = ( ctrl ,\mathfrak {K})\) where \( ctrl \) is an explicit control state and \(\mathfrak {K}\) is an epistemic state; then the state operator would be the projection to the second component, i.e. \(\varOmega (s) = \mathfrak {K}\). Our definition leaving control states implicit is, however, more general.
Of course, ensemble transitions must respect (up to bisimilarity) the epistemic effect of actions, which is expressed by condition 1a below. Conversely, if an epistemic ensemble action is enabled in an ensemble state, then all epistemic effects of the action must be present (up to bisimilarity) in the transition system, which is expressed by 1b. This reflects that the choice of the effect of a (non-deterministic) epistemic action is made by the system environment, not by the agents of the ensemble.
Note that different ensemble states can carry the same epistemic information, in particular if a non-epistemic agent action is performed. Then a transition between the two has a pure control flow effect. The set of ensemble states is restricted to states which are reachable by system transitions from the initial ones which is expressed by condition (2) below. This reflects our intuition that we want to consider ensembles as processes with significant dynamic behaviour. The restriction to reachable states and the ability to model control flow in the semantics is a crucial difference to dynamic epistemic logic; see, e.g., [6].
Definition 2 (Epistemic ensemble transition system)
Let \( \varSigma = ({P}, {A}, E )\) be an epistemic ensemble signature. An epistemic ensemble transition system (EETS) over \( \varSigma \) is a tuple \(M = (S, S_0, T, \varOmega )\) such that
-
S is a set of ensemble states and \(S_0 \subseteq S\) is the set of initial ensemble states,
-
\(T = (T_{ e } \subseteq S \times S)_{ e \in E }\) is an \( E \)-indexed family of transition relations \(T_e\), and
-
\(\varOmega : S \rightarrow EpiSt({P}, {A}) \) is an epistemic state operator
such that the following two conditions are satisfied:
-
1.
For all \(s \in S\) and \( e \in E \), if there exists \(s' \in S\) with \((s, s') \in T_{ e }\), then
-
(a)
there exist \(\mathfrak {K}, \mathfrak {K}' \in EpiSt({P}, {A}) \) such that \(\varOmega (s) \mathrel {\approx }\mathfrak {K}\), \(\varOmega (s') \mathrel {\approx }\mathfrak {K}'\), and \((\mathfrak {K},\mathfrak {K}') \in eeff ( e )\),
-
(b)
for any \((\mathfrak {K},\mathfrak {K}'') \in eeff ( e )\) there exists \((s, s'') \in T_{ e }\) with \(\varOmega (s) \mathrel {\approx }\mathfrak {K}\) and \(\varOmega (s'') \mathrel {\approx }\mathfrak {K}''\).
-
(a)
-
2.
For all \(s \in S\) there are \(s_0 \in S_0\), \( e _1,\ldots , e _n \in E \) (\(n \ge 0\)) and \((s_i,s_{i+1}) \in T_{e_i}\) for \(0 \le i < n\) such that \(s_n = s\).
The class of epistemic ensemble transition systems over \( \varSigma \) is denoted by \( Str ( \varSigma )\). \(\square \)
We write \(s \xrightarrow { e }_{M} s'\) for \((s, s') \in T_{ e }\). This relation is extended to compound epistemic ensemble actions \(\pi \in \mathcal {E}_{ \varSigma }\) by the following inductive definition:
For any epistemic ensemble signature \( \varSigma \), the satisfaction of an epistemic ensemble formula \(\psi \in \varPsi _{ \varSigma }\) by an EETS \(M = (S, S_0, T, \varOmega )\) over \( \varSigma \) at a state \(s \in S\), written \(M, s \models _{ \varSigma }\psi \), is inductively defined as follows:
M satisfies an epistemic ensemble formula \(\psi \in \varPsi _{ \varSigma }\), written \(M \models _{ \varSigma }\psi \), if \(M, s_0 \models _{ \varSigma }\psi \) for all initial states \(s_0 \in S_0\).
For the box, \(M, s \models _{ \varSigma }[\pi ]\psi \) means that whenever \(\pi \) is executed by the ensemble a state \(s'\) is reached in which \(\psi \) holds. Note that, if \(\pi = e\) is an atomic ensemble action such that the precondition \( pre (e)\) does not hold in \(\varOmega (s)\), then \(M, s \models _{ \varSigma }[e]\psi \) holds since there is no execution of e in state s.
Example 5
A connection to public announcement logic [3] can be drawn as follows: Consider the ensemble signature \( \varSigma = ({P}, {A}, E )\) with an arbitrary epistemic signature \(({P}, {A})\) and \( E \) consisting of all public announcements of the form \( pub ^{{a}}( \textsf{K} _{{a}}\!\mathop {}\varphi )\) with \({a}\in {A}\). As semantic model we take the special EETS \(M_\textrm{PAL} = ( EpiSt({P}, {A}) , EpiSt({P}, {A}) ,T,\varOmega )\) where the ensemble states are just the epistemic states over \(({P}, {A})\), all states are initial, \(T = (T_{ pub ^{{a}}( \textsf{K} _{{a}}\!\mathop {}\varphi )} \subseteq EpiSt({P}, {A}) \times EpiSt({P}, {A}) )_{ pub ^{{a}}( \textsf{K} _{{a}}\!\mathop {}\varphi ) \in E }\) with \(T_{ pub ^{{a}}( \textsf{K} _{{a}}\!\mathop {}\varphi )} = eeff ( pub ^{{a}}( \textsf{K} _{{a}}\!\mathop {}\varphi ))\) are the semantic transitions for public announcements, and \(\varOmega \) is the identity. Then, for any ensemble state s of \(M_\textrm{PAL}\), i.e. epistemic state \((K,w) \in EpiSt({P}, {A}) \), and any epistemic ensemble formula \(\psi \in \varPsi _{ \varSigma }\) we have \(M_\textrm{PAL}, (K,w) \models \psi \) if, and only if, (K, w) satisfies \(\psi \) in the sense of public announcement logic. \(\square \)
More generally, dynamic epistemic logic with arbitrary epistemic actions (U, q) such that \( pre (q)\) has the form \( \textsf{K} _{{a}}\!\mathop {}\varphi \) and \(o(U, q) = a \in {A}\) can be similarly interpreted by an EETS. Note, however, that in these cases no control information can be captured since ensemble states are just epistemic states. Therefore instead of stating requirements for ensemble behaviours these logics are more appropriate for the verification of pre- and postconditions of programs represented by compound ensemble actions where ensemble formulas have the shape \(\textrm{pre} \rightarrow [\pi ]\textrm{post}\).
Definition 3 (Semantics of epistemic ensemble specifications and refinement)
Let \( Sp = ( \varSigma , Ax )\) be an epistemic ensemble specification. A model of \( Sp \) is an EETS over \( \varSigma \) which satisfies all axioms of \( Ax \). The semantics of \( Sp \) is given by its model class
An epistemic ensemble specification \( Sp ' = ( \varSigma , Ax ')\) is a refinement of \( Sp \) if \(\textrm{Mod}( Sp ') \subseteq \textrm{Mod}( Sp )\). \(\square \)
As an equivalence for epistemic ensemble transition systems we use EETS-bisimulation which is defined as expected.
Definition 4 (Epistemic ensemble bisimulation)
Let \( \varSigma = ({P}, {A}, E )\) be an epistemic ensemble signature and \(M_1 = (S_1, S_{1,0}, T_1, \varOmega _1)\) and \(M_2 = (S_2, S_{2,0}, T_2, \varOmega _2)\) be two EETSs over \( \varSigma \). An EETS-bisimulation between \(M_1\) and \(M_2\) is a relation \( EB \subseteq S_1 \times S_2\) such that for all \((s_1, s_2) \in EB \) and all \( e \in E \) the following holds:
-
1.
\(\varOmega _1(s_1) \mathrel {\approx }\varOmega _2(s_2)\),
-
2.
for each \(s_1' \in S_1\), if \(s_1 \xrightarrow { e }_{M_1} s_1'\) then there is an \(s_2' \in S_2\) such that \(s_2 \xrightarrow { e }_{M_2} s_2'\) and \((s_1', s_2') \in EB \), and
-
3.
for each \(s_2' \in S_2\), if \(s_2 \xrightarrow { e }_{M_2} s_2'\) then there is an \(s_1' \in S_1\) such that \(s_1 \xrightarrow { e }_{M_1} s_1'\) and \((s_1', s_2') \in EB \).
\(M_1\) and \(M_2\) are EETS-bisimilar, written \(M_1 \sim M_2\), if there exists an EETS-bisimulation \( EB \) between \(M_1\) and \(M_2\) such that for each \(s_1 \in S_{1,0}\) there exists an \(s_2 \in S_{2,0}\) with \((s_1,s_2) \in EB \) and, conversely, for each \(s_2 \in S_{2,0}\) there exists an \(s_1 \in S_{1,0}\) with \((s_1,s_2) \in EB \). \(\square \)
It is easy to prove, by induction on the form of compound ensemble actions, that conditions (2) and (3) above can be propagated to compound ensemble actions \(\pi \in \mathcal {E}_{ \varSigma }\). As a consequence, it is straightforward to prove, by induction on the form of epistemic ensemble formulæ, that satisfaction is invariant under EETS-bisimulation. The base case follows from Lemma 1. The converse of the theorem is also valid for image-finite EETS.
Theorem 1 (Invariance of epistemic ensemble formulæ)
Let \(M_1\) and \(M_2\) be EETS over the same epistemic ensemble signature \( \varSigma \) such that \(M_1 \sim M_2\). Then, for any \(\psi \in \varPsi _{ \varSigma }\), \(M_1 \models \psi \) if, and only if, \(M_2 \models \psi \).
5 Epistemic Ensemble Realisations
Ensemble specifications describe requirements for systems of collaborating entities from a global point of view. For the realisation of ensembles we must take a local view and define a single behaviour for each agent. For this purpose, we introduce an epistemic process language over an epistemic ensemble signature \( \varSigma = ({P}, {A}, E )\) which allows us to describe the local behaviour of each agent \({a}\in {A}\) as a sequential process \(P_{{a}}\) in accordance with the following grammar:
where \(\textbf{0}\) represents the inactive process, \( e _{{a}}.P_{{a}}\) prefixes \(P_{{a}}\) with an agent action \( e _a \in E \), \(\varphi _{{a}} \supset P_{{a}}\) is a guarded process, \(P_{{a},1} + P_{{a}, 2}\) denotes the non-deterministic choice between processes, \(\mu X\,.\, P_{{a}}\) models recursion, and X is a process variable.
The following constraints apply to the syntax of processes: First, in a prefix \( e _{{a}}.P_{{a}}\) the owner of \( e _{{a}}\) must be \({a}\), i.e. \(o( e _{{a}}) = {a}\). Secondly, each agent \({a}\), or, more precisely, its process, shall only use guards concerning the agent’s own knowledge. We thus require \(\varphi _{{a}} \in \varPhi _{{P}, {A}}^{{a}}\); see Sect. 2.1. A similar constraint is applied to epistemic programs in [7].
Definition 5 (Epistemic ensemble realisation)
For an epistemic ensemble signature \( \varSigma = ({P}, {A}, E )\), an epistemic ensemble realisation over \( \varSigma \) is a pair \( Real = (\{P_{0,a} \mid {a}\in {A}\},\mathfrak {K}_0)\) where \(\{P_{0,a} \mid {a}\in {A}\}\) is a set of sequential processes over \( \varSigma \), one for each agent \({a}\in {A}\), and \(\mathfrak {K}_0 \in EpiSt({P}, {A}) \) is an initial epistemic state of the ensemble. \(\square \)
The semantics of an epistemic ensemble realisation is given in terms of en epistemic ensemble transition system. In this case the ensemble states are pairs \(s = ( ctrl ,\mathfrak {K})\) consisting of a global control state \( ctrl \) and an epistemic state \(\mathfrak {K}\in EpiSt({P}, {A}) \) capturing the current epistemic information of the ensemble. The control state \( ctrl \) holds the current (local) execution state of each agent represented by a process expression. Thus \( ctrl \) is a mapping that attaches to each \({a}\in {A}\) a sequential process \( ctrl (a) = P_{{a}}\). When an agent \({a}\) moves from one state \(P_{{a}}\) to another state \(P'_{{a}}\) the control state \( ctrl \) must be updated accordingly which is denoted by \( ctrl [a \mapsto P'_{{a}}]\).
In contrast to the loose semantics of ensemble specifications, an ensemble realisation \( Real = (\{P_{0,a} \mid {a}\in {A}\},\mathfrak {K}_0)\) determines a unique epistemic ensemble transition system. It has a single initial ensemble state \(s_0 = ( ctrl _0,\mathfrak {K}_0)\) where the control state \( ctrl _0\) assigns to each agent \({a}\) its process definition \(P_{0,a}\), i.e. \( ctrl _0({a}) = P_{0,a}\) for all \({a}\in {A}\). Then, starting in \(s_0\), an epistemic ensemble transition system is generated by the structural operational semantics rules in Fig. 1. For each ensemble state \(s = ( ctrl ,\mathfrak {K})\) of the system the epistemic state operator is defined by \(\varOmega ( ctrl ,\mathfrak {K}) = \mathfrak {K}\).
The first five rules, from (action prefix) to (recursion), describe how single processes evolve in the context of an epistemic state which (i) may change when the process performs an agent action and (ii) is used for the evaluation of guards. We use the symbol “ ” for transitions on the process level. Transitions on the ensemble level are denoted by “\(\xrightarrow {}\)”. Rule (ensemble) says that whenever a single agent process moves from a local process state \(P_{{a}}\) to state \(P'_{{a}}\) changing the epistemic state from \(\mathfrak {K}\) to \(\mathfrak {K}'\) the whole ensemble evolves accordingly.
” for transitions on the process level. Transitions on the ensemble level are denoted by “\(\xrightarrow {}\)”. Rule (ensemble) says that whenever a single agent process moves from a local process state \(P_{{a}}\) to state \(P'_{{a}}\) changing the epistemic state from \(\mathfrak {K}\) to \(\mathfrak {K}'\) the whole ensemble evolves accordingly.
Definition 6 (Semantics of an epistemic ensemble realisation)
The semantics of an epistemic ensemble realisation \( Real = (\{P_{0,{a}} \mid {a}\in {A}\},\mathfrak {K}_0)\) over an ensemble signature \( \varSigma \) is the epistemic ensemble transition system
over \( \varSigma \) where the initial ensemble state \(s_0\) and the state operator \(\varOmega \) are explained above and the states in S and transitions in T are inductively generated from \(s_0\) by applying the rules in Fig. 1. Note that \([\![ Real ]\!]\) satisfies the conditions of an EETS in Definition 2.
\(\square \)
Our semantic concepts lead to an obvious correctness notion concerning the realisation of epistemic ensemble specifications:
Definition 7 (Correct ensemble realisation)
Let \( Sp \) be an epistemic ensemble specification and let \( Real \) be a realisation over the same epistemic signature. \( Real \) is a correct realisation of \( Sp \) if \([\![ Real ]\!]\in \textrm{Mod}( Sp )\). \(\square \)
Example 6
We provide a realisation for our simple robot rescue ensemble with two agents \(\textrm{V}\) (victim) and \(\textrm{R}\) (rescuer). The realisation consists of the two processes
For the initial epistemic state of the realisation we take \(\mathfrak {K}_0 = (K_0,w_0)\) as depicted in Example 1. Thus the initial ensemble state is \(s_0 = ( ctrl _0, \mathfrak {K}_0)\) with \( ctrl _0(\textrm{V}) = P_{0,\textrm{V}}\), \( ctrl _0(\textrm{R}) = P_{0,\textrm{R}}\) and \(\varOmega (s_0) = \mathfrak {K}_0\). As long as the victim does not know that the rescuer knows that the victim needs help, the victim continues sending the information \( \textsf{K} _{\textrm{V}}\!\mathop {}\textrm{h}\) to the rescuer. Notice again that this sending is lossy and hence either successful or unsuccessful. Only when the rescuer became aware of the emergency it can send, in a reliable way, its knowledge to the victim who can then stop its activity.
The EETS generated from the ensemble realisation has infinitely many ensemble states since it is possible that an unsuccessful sending from \(\textrm{V}\) to \(\textrm{R}\) happens infinitely often and hence each time an update of the previous epistemic state is performed. One can show, however, that if an unsuccessful sending happens after an unsuccessful or successful sending then the resulting epistemic state is bisimilar to the previous one. Therefore, there exists a minimal finite EETS, shown in Fig. 2, which is EETS-bisimilar to the one generated by the ensemble realisation. The epistemic effect of lossy sending is non-deterministic. The transitions from ensemble state \(s_0\) to \(s_1\) and the loops on \(s_1\) and \(s_2\) represent unsuccessful transmissions and the transitions from \(s_0\) and from \(s_1\) to \(s_2\) represent successful ones. The associated epistemic states \((K_1,(w_0,\textsf{k}))\) and \((K_1,(w_0,\textsf{n}))\) are shown in Example 3. The epistemic state \((K_2,((w_0,\textsf{k}),\textsf{k}))\) associated with the ensemble states \(s_3\) to \(s_6\) is computed by updating \((K_1,(w_0,\textsf{k}))\) with the (deterministic) epistemic effect of the reliable sending from \(\textrm{R}\) to \(\textrm{V}\).
Obviously, the EETS in Fig. 2 satisfies the axioms of the specification \( Sp _{ vr }\) in Example 4. Therefore, according to Theorem 1, the bisimilar EETS generated from the epistemic ensemble realisation is a model of \( Sp _{ vr }\) and thus the realisation is correct w.r.t. \( Sp _{ vr }\). \(\square \)
Two epistemic ensemble realisations \( Real _1\) and \( Real _2\) over the same signature are called equivalent if \(\llbracket Real _1\rrbracket \sim \llbracket Real _2\rrbracket \). The following theorem says that for checking equivalence of epistemic ensemble realisations it is sufficient to show that their initial epistemic states are bisimilar and that the process definitions for each agent are pairwise bisimilar in the usual sense of process algebra; see e.g. [10]. We denote process bisimilarity by \(\sim _p \).
Theorem 2
Let \( Real _1 = (\{P^1_{0,a} \mid {a}\in {A}\},\mathfrak {K}^1_0)\) and \( Real _2 = (\{P^2_{0,a} \mid {a}\in {A}\},\mathfrak {K}^2_0)\) be two epistemic ensemble realisations over signature \( \varSigma \). If \(\mathfrak {K}^1_0 \mathrel {\approx }\mathfrak {K}^2_0\) and \(P^1_{0,a} \sim _p P^2_{0,a}\) for all \({a}\in {A}\), then \(\llbracket Real _1\rrbracket \sim \llbracket Real _2\rrbracket \).
Proof sketch. Let \(S_i\) be the ensemble states of \( Real _i\) for \(i = 1,2\). We use the relation \( EB \subseteq S_1 \times S_2\) such that \((( ctrl _1,\mathfrak {K}_1), ( ctrl _2,\mathfrak {K}_2)) \in EB \) iff \( ctrl _1(a) \sim _p ctrl _2(a)\) for all \({a}\in {A}\) and \(\mathfrak {K}_1 \mathrel {\approx }\mathfrak {K}_2\). By assumption, the initial ensemble states are related by \( EB \). We have to show that \( EB \) is an EETS-bisimulation.
Condition (1) of Definition 4 is satisfied by definition of \( EB \). For condition (2), let \((( ctrl _1,\mathfrak {K}_1), ( ctrl _2,\mathfrak {K}_2)) \in EB \) and \(( ctrl _1,\mathfrak {K}_1) \xrightarrow { e }_{\llbracket Real _1\rrbracket } ( ctrl _1',\mathfrak {K}_1')\). By rule (ensemble) in Fig. 1, there is  where \(P^1_{{a}} = ctrl _1({a})\) and \(P^{1'}_{{a}} = ctrl '_1({a})\). A case analysis on the form of \(P^1_{{a}}\) yields that
where \(P^1_{{a}} = ctrl _1({a})\) and \(P^{1'}_{{a}} = ctrl '_1({a})\). A case analysis on the form of \(P^1_{{a}}\) yields that  and \((\mathfrak {K}_1,\mathfrak {K}'_1) \in eeff ( e )\) where
and \((\mathfrak {K}_1,\mathfrak {K}'_1) \in eeff ( e )\) where  denotes process transition. Since \(\mathfrak {K}_1 \mathrel {\approx }\mathfrak {K}_2\), it follows from Lemma 3 that there is a \(\mathfrak {K}_2'\) such that \((\mathfrak {K}_2,\mathfrak {K}'_2) \in eeff ( e )\) and \(\mathfrak {K}_1' \mathrel {\approx }\mathfrak {K}_2'\). Let \(P^2_{{a}} = ctrl _2({a})\). Then \(P^1_{{a}} \sim _p P^2_{{a}}\) and therefore there exists
denotes process transition. Since \(\mathfrak {K}_1 \mathrel {\approx }\mathfrak {K}_2\), it follows from Lemma 3 that there is a \(\mathfrak {K}_2'\) such that \((\mathfrak {K}_2,\mathfrak {K}'_2) \in eeff ( e )\) and \(\mathfrak {K}_1' \mathrel {\approx }\mathfrak {K}_2'\). Let \(P^2_{{a}} = ctrl _2({a})\). Then \(P^1_{{a}} \sim _p P^2_{{a}}\) and therefore there exists  with \(P^{1'}_{{a}} \sim _p P^{2'}_{{a}}\). A case analysis on the form of \(P^2_{{a}}\) yields that
with \(P^{1'}_{{a}} \sim _p P^{2'}_{{a}}\). A case analysis on the form of \(P^2_{{a}}\) yields that  and hence, by rule (ensemble), that \(( ctrl _2,\mathfrak {K}_2) \xrightarrow { e }_{\llbracket Real _2\rrbracket } ( ctrl _2',\mathfrak {K}_2')\). Moreover, \((( ctrl _1',\mathfrak {K}_1'), ( ctrl _2',\mathfrak {K}_2')) \in EB \). \(\square \)
and hence, by rule (ensemble), that \(( ctrl _2,\mathfrak {K}_2) \xrightarrow { e }_{\llbracket Real _2\rrbracket } ( ctrl _2',\mathfrak {K}_2')\). Moreover, \((( ctrl _1',\mathfrak {K}_1'), ( ctrl _2',\mathfrak {K}_2')) \in EB \). \(\square \)
6 Conclusion
We have developed a formalism for rigorous specification and realisation of ensembles based on principles of epistemic logic and epistemic actions. A crucial difference to [5, 8, 9] is that agents in epistemic ensembles do not communicate by message passing, but information exchange is achieved implicitly by changing knowledge. Another approach with implicit interaction is provided by the DEECo component and ensemble model [4]. In this case a coordinator is responsible for triggering exchange of factual knowledge which is, however, not grounded in epistemic logic.
For specifications of bigger case-studies we would need to extend our logic to allow agent types, variables and quantification over agents. For ensemble realisations we want to go a step further and represent the epistemic information, that is currently used by agent processes by accessing a global epistemic state, by local knowledge bases attached to each agent process.
Notes
- 1.
We do not consider here completely private announcements where the agents not in G would not consider it possible that the announcement happened. To model this case one would need non-symmetric accessibility relations.
References
Baltag, A., Moss, L.S.: Logics for epistemic programs. Synthese 139(2), 165–224 (2004). https://doi.org/10.1023/B:SYNT.0000024912.56773.5e
Baltag, A., Moss, L.S., Solecki, S.: The logic of public announcements and common knowledge and private suspicions. In: Gilboa, I. (ed.) Proceedings of 7th Conference on Theoretical Aspects of Rationality and Knowledge (TARK 1998), pp. 43–56. Morgan Kaufmann (1998)
Baltag, A., Renne, B.: Dynamic epistemic logic. In: Zalta, E.N., Nodelman, U., Allen, C., Anderson, R.L. (eds.) Stanford Encyclopedia of Philosophy. The Metaphysics Research Lab, Stanford University (2016)
Bures, T., Gerostathopoulos, I., Hnetynka, P., Keznikl, J., Kit, M., Plasil, F.: DEECO: an ensemble-based component system. In: Kruchten, P., Giannakopoulou, D., Tivoli, M. (eds.) Proceedings of 16th ACM SIGSOFT Symposium on Component Based Software Engineering (CBSE 2013), pp. 81–90. ACM (2013). https://doi.org/10.1145/2465449.2465462
De Nicola, R., Loreti, M., Pugliese, R., Tiezzi, F.: A formal approach to autonomic systems programming: the SCEL language. ACM Trans. Auton. Adapt. Syst. (TAAS) 9(2), 1–29 (2014). https://doi.org/10.1145/2619998
van Ditmarsch, H., van der Hoek, W., Kooi, B.: Dynamic Epistemic Logic. Synthese Library, vol. 337. Springer, Cham (2008). https://doi.org/10.1007/978-1-4020-5839-4
Fagin, R., Halpern, J.Y., Moses, Y., Vardi, M.Y.: Reasoning About Knowledge. MIT Press, Cambridge (2003)
Hennicker, R., Wirsing, M.: Dynamic logic for ensembles. In: Margaria, T., Steffen, B. (eds.) ISoLA 2018. LNCS, vol. 11246, pp. 32–47. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03424-5_3
Hennicker, R., Wirsing, M.: A dynamic logic for systems with predicate-based communication. In: Margaria, T., Steffen, B. (eds.) ISoLA 2020. LNCS, vol. 12477, pp. 224–242. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-61470-6_14
Milner, R.: Communication and concurrency. PHI Series in computer science, Prentice Hall (1989)
Pinciroli, C., Bonani, M., Mondada, F., Dorigo, M.: Adaptation and awareness in robot ensembles: scenarios and algorithms. In: Wirsing, M., Hölzl, M., Koch, N., Mayer, P. (eds.) Software Engineering for Collective Autonomic Systems. LNCS, vol. 8998, pp. 471–494. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16310-9_15
Sürmeli, J.: Epistemic logic in ensemble specification. In: Margaria, T., Steffen, B. (eds.) ISoLA 2020. LNCS, vol. 12477, pp. 329–343. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-61470-6_20
Wirsing, M., Banâtre, J.-P., Hölzl, M., Rauschmayer, A. (eds.): Software-Intensive Systems and New Computing Paradigms. LNCS, vol. 5380. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89437-7
Hölzl, M., Koch, N., Puviani, M., Wirsing, M., Zambonelli, F.: The ensemble development life cycle and best practices for collective autonomic systems. In: Wirsing, M., Hölzl, M., Koch, N., Mayer, P. (eds.) Software Engineering for Collective Autonomic Systems. LNCS, vol. 8998, pp. 325–354. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16310-9_9
Wirsing, M., Hölzl, M., Tribastone, M., Zambonelli, F.: ASCENS: engineering autonomic service-component ensembles. In: Beckert, B., Damiani, F., de Boer, F.S., Bonsangue, M.M. (eds.) FMCO 2011. LNCS, vol. 7542, pp. 1–24. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-35887-6_1
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this paper
Cite this paper
Hennicker, R., Knapp, A., Wirsing, M. (2022). Epistemic Ensembles. In: Margaria, T., Steffen, B. (eds) Leveraging Applications of Formal Methods, Verification and Validation. Adaptation and Learning. ISoLA 2022. Lecture Notes in Computer Science, vol 13703. Springer, Cham. https://doi.org/10.1007/978-3-031-19759-8_8
Download citation
DOI: https://doi.org/10.1007/978-3-031-19759-8_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-19758-1
Online ISBN: 978-3-031-19759-8
eBook Packages: Computer ScienceComputer Science (R0)