Continuous Wavelet Transform for Severity-Level Classification of Dysarthria

Abstract

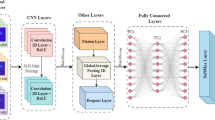
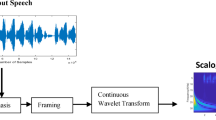
Dysarthria is a neuro-motor speech defect that causes speech to be unintelligible and is largely unnoticeable to humans at various severity-levels. Dysarthric speech classification is used as a diagnostic method to assess the progression of a patient’s severity of the condition, as well as to aid with automatic dysarthric speech recognition systems (an important assistive speech technology). This study investigates the significance of Generalized Morse Wavelet (GMW)-based scalogram features for capturing the discriminative acoustic cues of dysarthric severity-level classification for low-frequency regions, using Convolutional Neural Network (CNN). The performance of scalogram-based features is compared with Short-Time Fourier Transform (STFT)-based features, and Mel spectrogram-based features. Compared to the STFT-based baseline features with a classification accuracy of $91.76\%$, the proposed Continuous Wavelet Transform (CWT)-based scalogram features achieve significantly improved classification accuracy of $95.17\%$ on standard and statistically meaningful UA-Speech corpus. The remarkably improved results signify that for better dysarthric severity-level classification, the information in the low-frequency regions is more discriminative, as the proposed CWT-based time-frequency representation (scalogram) has a high-frequency resolution in the lower frequencies. On the other hand, STFT-based representations have constant resolution across all the frequency bands and therefore, are not as better suited for dysarthric severity-level classification, as the proposed Morse wavelet-based CWT features. In addition, we also perform experiments on the Mel spectrogram to demonstrate that even though the Mel spectrogram also has a high frequency resolution in the lower frequencies with a classification accuracy of $92.65\%$, the proposed system is better suited. We see an increase of $3.41\%$ and $2.52\%$ in classification accuracy of the proposed system to STFT and Mel spectrogram respectively. To that effect, the performance of the STFT, Mel spectrogram, and scalogram are analyzed using F1-Score, Matthew’s Correlation Coefficients (MCC), Jaccard Index, Hamming Loss, and Linear Discriminant Analysis (LDA) scatter plots.

Appendix

A.1. Energy Conservation in STFT

The energy conservation in STFT for any signal $f(t)\in L^2(R)$ is given by

$$\begin{aligned} \int _{-\infty }^{+\infty } |f(t)|^2 dt=\frac{1}{2\pi }\int _{-\infty }^{+\infty }\int _{-\infty }^{+\infty }|Sf(u,\zeta )|^2 d\zeta du, \end{aligned}$$

(16)

Here, u and $\zeta$ indicate the time-frequency indices that vary across R and hence, covers the entire time-frequency plane. The reconstruction of signal can then be given by

$$\begin{aligned} f(t)=\frac{1}{2\pi }\int _{-\infty }^{+\infty }\int _{-\infty }^{+\infty } Sf(u,\zeta )g(t-u)e^{i\zeta t}d\zeta du. \end{aligned}$$

(17)

Applying Parseval’s formula to Eq. (17) w.r.t. to the integration in u, we get

$$\begin{aligned} Sf(u,\zeta )=e^{-iu\zeta }f*g_\zeta (u), \end{aligned}$$

(18)

Here, $g_{\zeta }(t)=g(t)e^{i\zeta t}$. Hence, Fourier Transform of $Sf(u,\zeta )$ is $\hat{f}(\omega _ \zeta )\hat{g}(\omega )$. Furthermore, after applying the Plancherel’s formula to Eq. (16) gives

$$\begin{aligned} \frac{1}{2\pi }\int _{-\infty }^{+\infty }\int _{-\infty }^{+\infty }|Sf(u,\zeta )|^2 du d\zeta = \frac{1}{2\pi }\int _{-\infty }^{+\infty } \frac{1}{2\pi }\int _{-\infty }^{+\infty } |\hat{f}(\omega + \zeta )\hat{g}(\omega )|^2d\omega d\zeta . \end{aligned}$$

(19)

Finally, the Plancheral formula and the Fubini theorem result in $\frac{1}{2\pi }\int _{-\infty }^{+\infty }|\hat{f}(\omega +\zeta )|^2 d\zeta =||f||^2$, which validates STFT’s energy conservation as demonstrated in Eq. (16), It explains why the overall signal energy is the same as the time-frequency sum of the STFT.

A.2. Energy Conservation in CWT

Using the same derivations as in the discussion of Eq. 17, one can verify that the inverse wavelet formula reconstructs the analytic part of f : 

$$\begin{aligned} f_a(t) = \frac{1}{C_{\psi }}\int _{0}^{+\infty } \int _{-\infty }^{+\infty }Wf_a(u,s)\psi _{s}(t-u) \frac{ds}{s^2}du. \end{aligned}$$

(20)

Applying the Plancherel formula for energy conservation for the analytic part of $f_a$ given by

$$\begin{aligned} \int _{-\infty }^{+\infty }|f_a(t)|^2dt = \frac{1}{C_{\psi }} \int _{0}^{+\infty } \int _{-\infty }^{+\infty }|W_af(u,s)|^2du \frac{ds}{s^2}. \end{aligned}$$

(21)

Since $Wf_a(u,s)$ = 2Wf(u, s) and $||f_a||^2$ = $2||f||^2$.

If f is real, and the variable change $\zeta$ = $\frac{1}{s}$ in energy conservation denotes that

$$\begin{aligned} ||f||^2 = \frac{2}{C_{\psi }} \int _{0}^{+\infty } \int _{-\infty }^{+\infty } P_w f(u, \zeta )dud\zeta . \end{aligned}$$

(22)

It reinforces the notion that a scalogram represents a time-frequency energy density.