Skip to main content
Springer Nature Link
Log in

Card-Based Zero-Knowledge Proof for the Nearest Neighbor Property: Zero-Knowledge Proof of ABC End View

  • Conference paper
  • First Online:
Security, Privacy, and Applied Cryptography Engineering (SPACE 2022)

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 13783))

  • 475 Accesses

Abstract

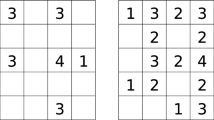
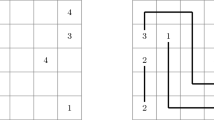
This paper shows a zero-knowledge proof protocol of a solution to ABC end view puzzle using physical cards. Card-based cryptographic protocols are proposed to execute a secure multi-party calculation using physical cards instead of computers. This paper shows a card-based zero-knowledge proof of the ABC end view puzzle. The puzzle needs a new technique to prove the nearest neighbor from an end. We show a new zero-knowledge proof protocol to securely calculate the nearest neighbor using physical cards.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

Notes

  1. 1.

    It is unnecessary to divide the piles as z(1) and \(z[2-]\). We set \(y_j(1), y_j(2), z, y_j\) in this order, swap the second and the third, execute a random bisection cut, swap the second and the third, open the left two cards, and obtain the result as the AND protocol. The result is the same as the protocol shown in this paper.

References

  1. Abe, Y., et al.: Efficient card-based majority voting protocols. New Gener. Comput. 40(1), 173–198 (2022)

    Article  Google Scholar 

  2. den Boer, B.: More efficient match-making and satisfiability The Five Card Trick. In: Quisquater, J.-J., Vandewalle, J. (eds.) EUROCRYPT 1989. LNCS, vol. 434, pp. 208–217. Springer, Heidelberg (1990). https://doi.org/10.1007/3-540-46885-4_23

    Chapter  Google Scholar 

  3. Bultel, X., Dreier, J., Dumas, J.G., Lafourcade, P.: Physical zero-knowledge proofs for Akari, Takuzu, Kakuro and Kenken. In: Proceedings of 8th International Conference on Fun with Algorithms, vol. 49, pp. 1–8. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2016)

    Google Scholar 

  4. Bultel, X., et al.: Physical zero-knowledge proof for Makaro. In: Izumi, T., Kuznetsov, P. (eds.) SSS 2018. LNCS, vol. 11201, pp. 111–125. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03232-6_8

    Chapter  Google Scholar 

  5. Chien, Y.-F., Hon, W.-K.: Cryptographic and physical zero-knowledge proof: from Sudoku to Nonogram. In: Boldi, P., Gargano, L. (eds.) FUN 2010. LNCS, vol. 6099, pp. 102–112. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13122-6_12

    Chapter  Google Scholar 

  6. crossa@list.ru: Puzzles: Abc end view. http://www.cross-plus-a.com/puzzles.htm#EasyAsABC. Accessed 31 Aug 2022

  7. Dumas, J.-G., Lafourcade, P., Miyahara, D., Mizuki, T., Sasaki, T., Sone, H.: Interactive Physical Zero-Knowledge Proof for Norinori. In: Du, D.-Z., Duan, Z., Tian, C. (eds.) COCOON 2019. LNCS, vol. 11653, pp. 166–177. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26176-4_14

    Chapter  Google Scholar 

  8. Gradwohl, R., Naor, M., Pinkas, B., Rothblum, G.N.: Cryptographic and physical zero-knowledge proof systems for solutions of Sudoku puzzles. Theor. Comput. Syst. 44(2), 245–268 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  9. Hart, E., McGinnis, J.A.: Physical zero-knowledge proofs for flow free, Hamiltonian cycles, and many-to-many k-disjoint covering paths (2022) arXiv preprint arXiv:2202.04113

  10. Kastner, J., et al.: The minimum number of cards in practical card-based protocols. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10626, pp. 126–155. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_5

    Chapter  Google Scholar 

  11. Komano, Y., Mizuki, T.: Physical zero-knowledge proof protocol for topswops. In: Proceedings of 17th International Conference on Information Security Practice and Experience (ISPEC 2022), LNCS. Springer (2022) https://doi.org/10.1007/978-3-031-21280-2_30

  12. Lafourcade, P., Miyahara, D., Mizuki, T., Robert, L., Sasaki, T., Sone, H.: How to construct physical zero-knowledge proofs for puzzles with a “single loop” condition. Theor. Comput. Sci. 888, 41–55 (2021)

    Google Scholar 

  13. Manabe, Y.: Survey: card-based cryptographic protocols to calculate primitives of boolean functions. Int. J. Comput. Softw. Eng. 27(1), 178 (2022)

    Google Scholar 

  14. Miyahara, D., Hayashi, Y.I., Mizuki, T., Sone, H.: Practical card-based implementations of Yao’s millionaire protocol. Theoret. Comput. Sci. 803, 207–221 (2020)

    Google Scholar 

  15. Miyahara, D., et al.: Card-based ZKP protocols for Takuzu and Juosan. In: Proceedings of 10th International Conference on Fun with Algorithms (FUN 2020). Schloss Dagstuhl-Leibniz-Zentrum für Informatik (2020)

    Google Scholar 

  16. Miyahara, D., Sasaki, T., Mizuki, T., Sone, H.: Card-based physical zero-knowledge proof for kakuro. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 102(9), 1072–1078 (2019)

    Article  Google Scholar 

  17. Mizuki, T., Asiedu, I.K., Sone, H.: Voting with a logarithmic number of cards. In: Mauri, G., Dennunzio, A., Manzoni, L., Porreca, A.E. (eds.) UCNC 2013. LNCS, vol. 7956, pp. 162–173. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39074-6_16

    Chapter  Google Scholar 

  18. Mizuki, T., Shizuya, H.: A formalization of card-based cryptographic protocols via abstract machine. Int. J. Inf. Secur. 13(1), 15–23 (2014)

    Article  Google Scholar 

  19. Mizuki, T., Sone, H.: Six-card secure AND and four-card secure XOR. In: Deng, X., Hopcroft, J.E., Xue, J. (eds.) FAW 2009. LNCS, vol. 5598, pp. 358–369. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02270-8_36

    Chapter  Google Scholar 

  20. Nakai, Takeshi, Misawa, Yuto, Tokushige, Yuuki, Iwamoto, Mitsugu, Ohta, Kazuo: How to Solve Millionaires’ Problem with Two Kinds of Cards. New Gener. Comput. 39(1), 73–96 (2021). https://doi.org/10.1007/s00354-020-00118-8

    Article  Google Scholar 

  21. Ono, H., Manabe, Y.: Efficient card-based cryptographic protocols for the millionaires problem using private input operations. In: Proceedings of 13th Asia Joint Conference on Information Security(AsiaJCIS 2018), pp. 23–28 (2018)

    Google Scholar 

  22. Robert, L., Miyahara, D., Lafourcade, P., Libralesso, L., Mizuki, T.: Physical zero-knowledge proof and np-completeness proof of Suguru puzzle. Inf. Comput. 285, 104858 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  23. Robert, L., Miyahara, D., Lafourcade, P., Mizuki, T.: Card-based ZKP for connectivity: applications to nurikabe, Hitori and Heyawake. New Gener. Comput. 40(1), 149–171 (2022)

    Google Scholar 

  24. Robert, L., Miyahara, D., Lafourcade, P., Mizuki, T.: Card-based ZKP protocol for Nurimisaki. In: Proceedings of 24th International Symposium on Stabilization, Safety, and Security of Distributed Systems (SSS 2022), LNCS. Springer (2022)

    Google Scholar 

  25. Ruangwises, S.: An improved physical ZKP for nonogram. arXiv preprint arXiv:2106.14020 (2021)

  26. Ruangwises, S.: Two standard decks of playing cards are sufficient for a ZKP for sudoku. New Gener. Comput. 40(1), 49–65 (2022)

    Article  Google Scholar 

  27. Ruangwises, Suthee, Itoh, Toshiya: Physical Zero-Knowledge Proof for Number link Puzzle and k Vertex-Disjoint Paths Problem. New Generation Computing 39(1), 3–17 (2021). https://doi.org/10.1007/s00354-020-00114-y

    Article  Google Scholar 

  28. Ruangwises, Suthee, Itoh, Toshiya: Physical zero-knowledge proof for Ripple Effect. Theor. Comput. Sci. 895, 115–123 (2021). https://doi.org/10.1016/j.tcs.2021.09.034

    Article  MathSciNet  MATH  Google Scholar 

  29. Ruangwises, S., Itoh, T.: Physical ZKP for Makaro using a standard deck of cards. arXiv preprint arXiv:2112.12042 (2021)

  30. Ruangwises, S., Itoh, T.: How to physically verify a rectangle in a grid: a physical ZKP for shikaku (2022). arXiv preprint arXiv:2202.09788

  31. Sasaki, T., Miyahara, D., Mizuki, T., Sone, H.: Efficient card-based zero-knowledge proof for Sudoku. Theoret. Comput. Sci. 839, 135–142 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  32. Shinagawa, Kazumasa, Nuida, Koji: A single shuffle is enough for secure card-based computation of any Boolean circuit. Discrete Applied Mathematics 289, 248–261 (2021). https://doi.org/10.1016/j.dam.2020.10.013

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Kogakuin University, Shinjuku, Tokyo, 163-8677, Japan

    Takuro Fukasawa & Yoshifumi Manabe

Authors
  1. Takuro Fukasawa
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yoshifumi Manabe
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yoshifumi Manabe .

Editor information

Editors and Affiliations

  1. Radboud University, Nijmegen, The Netherlands

    Lejla Batina

  2. Radboud University, Nijmegen, The Netherlands

    Stjepan Picek

  3. Indian Institute of Technology Kharagpur, Kharagpur, India

    Mainack Mondal

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Fukasawa, T., Manabe, Y. (2022). Card-Based Zero-Knowledge Proof for the Nearest Neighbor Property: Zero-Knowledge Proof of ABC End View. In: Batina, L., Picek, S., Mondal, M. (eds) Security, Privacy, and Applied Cryptography Engineering. SPACE 2022. Lecture Notes in Computer Science, vol 13783. Springer, Cham. https://doi.org/10.1007/978-3-031-22829-2_9

Download citation

  • DOI: https://doi.org/10.1007/978-3-031-22829-2_9

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-031-22828-5

  • Online ISBN: 978-3-031-22829-2

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics