New Algorithm for Exhausting Optimal Permutations for Generalized Feistel Networks

Abstract

The Feistel construction is one of the most studied ways of building block ciphers. Several generalizations were proposed in the literature, leading to the Generalized Feistel Network (GFN) construction, in which the round function operates on each pair of blocks in parallel until all branches are permuted. At FSE’10, Suzaki and Minematsu studied the diffusion of such construction, raising the question of how many rounds are required so that each block of the ciphertext depends on all blocks of the plaintext. Exhausting all possible permutations up to 16 blocks, they observed that there were always optimal permutations mapping even-number input blocks to odd-number output blocks and vice versa. Recently, both Cauchois et al. and Derbez et al. proposed new algorithms to build optimal even-odd permutations for up to 36 blocks. In this paper, we present a new algorithm based on iterative path building to search for optimal Feistel permutation. This algorithm is much faster in exhausting optimal non-even-odd permutations than all the previous approaches. Our first result is a computational proof that no non-even-odd permutation reaches a better diffusion round than optimal even-odd permutations up to 32 blocks. Furthermore, it is well known that permutations with an optimal diffusion round do not always lead to optimal permutations against differential cryptanalysis. We investigate several new criteria to build permutations leading to more secure GFN.

The work presented in this article was funded by the French National Research Agency as part of the DeCrypt project (ANR- 18-CE39-0007).

Appendix a Proofs of Proposition 3 and 4

Proposition 3. Let $\pi$ be an even-odd permutation $\pi$, X-$DR(\pi )$ is the smallest integer R such that: $\forall c\in {V_{\textsf{o}}}, d\in {V_{\textsf{e}}}$, there are X paths of length $R-3$ from c to d in $G_\pi$.

Proof

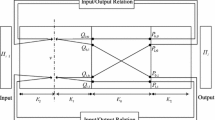
Let $b,c\in {V_{\textsf{o}}}$ and $a,d\in {V_{\textsf{e}}}$ with $(a,c),(d,b)\in E_{\pi }$. We have that $(a+1,a),(b,b-1)\in E_{\epsilon }$ with $a+1\in {V_{\textsf{o}}}$ and $b-1\in {V_{\textsf{e}}}$. Furthermore, we have $g,h\in V$ such that $(b,g),(b-1,h)\in E_{\pi }$ (see the graph below with $i=a+1$ and $j=b-1$).

1) From Definition 8, we know that there is X d-paths of length R from a to g, thus there is X paths of length $R-3$ from c to d.

2) Now suppose that there is $R'<X$-$DR(\pi )$ such that $\forall ~ c\in {V_{\textsf{o}}},~ d\in {V_{\textsf{e}}}$ there is X paths of length $R'-3$ from c to d. We then have X d-paths of length $R'$ from i to g, from i to h and from a to h. Since we have these d-paths for all pairs $a\in {V_{\textsf{e}}}, b\in {V_{\textsf{o}}}$ then we have full diffusion with X-$DR(\pi )=R'$ and thus the contradiction X-$DR(\pi )<X$-$DR(\pi )$.    $\square$

Proposition 4. Let $\pi$ be an even-odd permutation $\pi$, X-$SB(\pi )$ is the smallest integer R such that: $\forall c\in {V_{\textsf{o}}}, d\in {V_{\textsf{e}}}$, there are X S-Boxes traversed by paths of length $R-3$ from c to d in $G_\pi$. A S-Box reached by two paths at the same time will be counted only once.

Proof

Let $b,c\in {V_{\textsf{o}}}$ and $a,d\in {V_{\textsf{e}}}$ with $(a,c),(d,b)\in E_{\pi }$. We have that $(a+1,a),(b,b-1)\in E_{\epsilon }$ with $a+1\in {V_{\textsf{o}}}$ and $b-1\in {V_{\textsf{e}}}$. Furthermore, we have $g,h\in V$ such that $(b,g),(b-1,h)\in E_{\pi }$ (see the graph below with $i=a+1$ and $j=b-1$).

1) From Definition 9, we know that there is X S-Boxes in all the d-paths of length R from a to g, thus there is X S-Boxes in all paths of length $R-3$ from c to d.

2) Now suppose that there is $R'<X$-$SB(\pi )$ such that $\forall ~ c\in {V_{\textsf{o}}},~ d\in {V_{\textsf{e}}}$ there is X S-Boxes in all the paths of length $R'-3$ from c to d. We then have X S-Boxes in all the d-paths of length $R'$ from i to g, from i to h and from a to h. Since we have these d-paths for all pairs $a\in {V_{\textsf{e}}}, b\in {V_{\textsf{o}}}$ then we have full diffusion with X-$SB(\pi )=R'$ and thus the contradiction X-$SB(\pi )<X$-$SB(\pi )$.

   $\square$