Skip to main content
Springer Nature Link
Log in

Minimizing Even-Mansour Ciphers for Sequential Indifferentiability (Without Key Schedules)

  • Conference paper
  • First Online:
Progress in Cryptology – INDOCRYPT 2022 (INDOCRYPT 2022)

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 13774))

Included in the following conference series:

  • 501 Accesses

Abstract

Iterated Even-Mansour (IEM) schemes consist of a small number of fixed permutations separated by round key additions. They enjoy provable security, assuming the permutations are public and random. In particular, regarding chosen-key security in the sense of sequential indifferentiability (seq-indifferentiability), Cogliati and Seurin (EUROCRYPT 2015) showed that without key schedule functions, the 4-round Even-Mansour with Independent Permutations and no key schedule \(\text {EMIP} _4(k,u) = k \oplus \textbf{p} _4\big ( k \oplus \textbf{p} _3\big ( k \oplus \textbf{p} _2( k\oplus \textbf{p} _1(k \oplus u) ) \big ) \big )\) is sequentially indifferentiable.

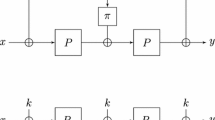
Minimizing IEM variants for classical strong (tweakable) pseudorandom security has stimulated an attractive line of research. In this paper, we seek for minimizing the \(\text {EMIP} _4\) construction while retaining seq-indifferentiability. We first consider \(\text {EMSP}\), a natural variant of \(\text {EMIP}\) using a single round permutation. Unfortunately, we exhibit a slide attack against \(\text {EMSP}\) with any number of rounds. In light of this, we show that the 4-round \(\text {EM2P}_4^{\textbf{p} _1,\textbf{p} _2} (k,u)=k\oplus \textbf{p} _1\big (k \oplus \textbf{p} _2\big (k\oplus \textbf{p} _2(k\oplus \textbf{p} _1(k\oplus u))\big )\big )\) using 2 independent random permutations \(\textbf{p} _1,\textbf{p} _2\) is seq-indifferentiable. This provides the minimal seq-indifferentiable IEM without key schedule.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

Notes

  1. 1.

    In comparison, Cogliati and Seurin’s simulator for \(\text {EMIP}_4\) completes all newly constituted pairs \(\big ((2,x_2,y_2),(3,x_3,y_3)\big )\) of records of \(P_2\) and \(P_3\).

References

  1. Andreeva, E., Bogdanov, A., Dodis, Y., Mennink, B., Steinberger, J.P.: On the indifferentiability of key-alternating ciphers. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 531–550. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_29

    Chapter  Google Scholar 

  2. Andreeva, E., Bogdanov, A., Mennink, B.: Towards understanding the known-key security of block ciphers. In: Moriai, S. (ed.) FSE 2013. LNCS, vol. 8424, pp. 348–366. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43933-3_18

    Chapter  Google Scholar 

  3. Biryukov, A., Wagner, D.: Slide attacks. In: Knudsen, L. (ed.) FSE 1999. LNCS, vol. 1636, pp. 245–259. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48519-8_18

    Chapter  Google Scholar 

  4. Bogdanov, A., Knudsen, L.R., Leander, G., Standaert, F.-X., Steinberger, J., Tischhauser, E.: Key-alternating ciphers in a provable setting: encryption using a small number of public permutations. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 45–62. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_5

    Chapter  MATH  Google Scholar 

  5. Canetti, R., Goldreich, O., Halevi, S.: The random oracle methodology, revisited. J. ACM 51(4), 557–594 (2004). https://doi.org/10.1145/1008731.1008734

  6. Chen, S., Lampe, R., Lee, J., Seurin, Y., Steinberger, J.: Minimizing the two-round even–mansour cipher. J. Cryptol. 31(4), 1064–1119 (2018). https://doi.org/10.1007/s00145-018-9295-y

    Article  MathSciNet  MATH  Google Scholar 

  7. Chen, S., Steinberger, J.P.: Tight security bounds for key-alternating ciphers. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 327–350. Springer, Heidelberg (May 2014). https://doi.org/10.1007/978-3-642-55220-5_19

  8. Cogliati, B., Seurin, Y.: On the provable security of the iterated even-mansour cipher against related-key and chosen-key attacks. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 584–613. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_23

    Chapter  Google Scholar 

  9. Cogliati, B., Seurin, Y.: Strengthening the known-key security notion for block ciphers. In: Peyrin, T. (ed.) FSE 2016. LNCS, vol. 9783, pp. 494–513. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-52993-5_25

    Chapter  Google Scholar 

  10. Coron, J.-S., Dodis, Y., Malinaud, C., Puniya, P.: Merkle-Damgård revisited: how to construct a hash function. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 430–448. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_26

    Chapter  Google Scholar 

  11. Coron, J.-S., Holenstein, T., Künzler, R., Patarin, J., Seurin, Y., Tessaro, S.: How to build an ideal cipher: the indifferentiability of the feistel construction. J. Cryptol. 29(1), 61–114 (2014). https://doi.org/10.1007/s00145-014-9189-6

    Article  MathSciNet  MATH  Google Scholar 

  12. Dachman-Soled, D., Katz, J., Thiruvengadam, A.: 10-round feistel is indifferentiable from an ideal cipher. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 649–678. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_23

    Chapter  Google Scholar 

  13. Dai, Y., Seurin, Y., Steinberger, J., Thiruvengadam, A.: Indifferentiability of iterated even-mansour ciphers with non-idealized key-schedules: five rounds are necessary and sufficient. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 524–555. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_18

    Chapter  Google Scholar 

  14. Dai, Y., Steinberger, J.: Indifferentiability of 8-round feistel networks. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 95–120. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_4

    Chapter  Google Scholar 

  15. Dodis, Y., Ristenpart, T., Steinberger, J., Tessaro, S.: To hash or not to hash again? (in)differentiability results for H2 and HMAC. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 348–366. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_21

    Chapter  MATH  Google Scholar 

  16. Dodis, Y., Stam, M., Steinberger, J., Liu, T.: Indifferentiability of confusion-diffusion networks. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 679–704. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_24

    Chapter  Google Scholar 

  17. Dunkelman, O., Keller, N., Shamir, A.: Minimalism in cryptography: the even-mansour scheme revisited. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 336–354. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_21

    Chapter  MATH  Google Scholar 

  18. Dutta, A.: Minimizing the two-round tweakable even-mansour cipher. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020. LNCS, vol. 12491, pp. 601–629. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64837-4_20

    Chapter  Google Scholar 

  19. Even, S., Mansour, Y.: A construction of a cipher from a single pseudorandom permutation. J. Cryptol. 10(3), 151–161 (1997). https://doi.org/10.1007/s001459900025

    Article  MathSciNet  MATH  Google Scholar 

  20. Farshim, P., Procter, G.: The related-key security of iterated even–mansour ciphers. In: Leander, G. (ed.) FSE 2015. LNCS, vol. 9054, pp. 342–363. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48116-5_17

    Chapter  Google Scholar 

  21. Guo, C., Lin, D.: A synthetic indifferentiability analysis of interleaved double-key even-mansour ciphers. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9453, pp. 389–410. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48800-3_16

    Chapter  Google Scholar 

  22. Guo, C., Lin, D.: Indifferentiability of 3-round even-mansour with random oracle key derivation. IACR Cryptol. ePrint Arch, p. 894 (2016). http://eprint.iacr.org/2016/894

  23. Guo, C., Lin, D.: Separating invertible key derivations from non-invertible ones: sequential indifferentiability of 3-round even-mansour. Des. Codes Crypt. 81(1), 109–129 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  24. Guo, J., Peyrin, T., Poschmann, A., Robshaw, M.: The LED block cipher. In: Preneel, B., Takagi, T. (eds.) CHES 2011. LNCS, vol. 6917, pp. 326–341. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-23951-9_22

    Chapter  Google Scholar 

  25. Hoang, V.T., Tessaro, S.: Key-alternating ciphers and key-length extension: exact bounds and multi-user security. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 3–32. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_1

    Chapter  Google Scholar 

  26. ISO/IEC: Information technology — security techniques – lightweight cryptography – part 2: Block ciphers. ISO/IEC 29192-2:2012 (2012). https://www.iso.org/standard/56552.html

  27. ISO/IEC: Information security – encryption algorithms – part 7: Tweakable block ciphers. ISO/IEC FDIS 18033-7 (2021). https://www.iso.org/standard/80505.html

  28. Lampe, R., Patarin, J., Seurin, Y.: An asymptotically tight security analysis of the iterated even-mansour cipher. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 278–295. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_18

    Chapter  Google Scholar 

  29. Lampe, R., Seurin, Y.: How to construct an ideal cipher from a small set of public permutations. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 444–463. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_23

    Chapter  Google Scholar 

  30. Mandal, A., Patarin, J., Seurin, Y.: On the public indifferentiability and correlation intractability of the 6-round feistel construction. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 285–302. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_16

    Chapter  MATH  Google Scholar 

  31. Maurer, U., Renner, R., Holenstein, C.: Indifferentiability, impossibility results on reductions, and applications to the random oracle methodology. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 21–39. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_2

    Chapter  Google Scholar 

  32. Mouha, N., Luykx, A.: Multi-key security: the even-mansour construction revisited. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 209–223. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_10

    Chapter  Google Scholar 

  33. Pub, N.F.: 197: Advanced encryption standard (aes). Federal Inf. Process. Stand. Publication 197(441), 0311 (2001)

    Google Scholar 

  34. Soni, P., Tessaro, S.: Public-seed pseudorandom permutations. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 412–441. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_14

    Chapter  Google Scholar 

  35. Soni, P., Tessaro, S.: Naor-reingold goes public: the complexity of known-key security. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10822, pp. 653–684. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_21

    Chapter  Google Scholar 

  36. Tessaro, S., Zhang, X.: Tight security for key-alternating ciphers with correlated sub-keys. In: Tibouchi, M., Wang, H. (eds.) Advances in Cryptology - ASIACRYPT 2021, Part III. Lecture Notes in Computer Science, vol. 13092, pp. 435–464. Springer (2021). https://doi.org/10.1007/978-3-030-92078-4

  37. Wu, Y., Yu, L., Cao, Z., Dong, X.: Tight security analysis of 3-round key-alternating cipher with a single permutation. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020. LNCS, vol. 12491, pp. 662–693. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64837-4_22

    Chapter  Google Scholar 

Download references

Acknowledgements

We sincerely thank the anonymous reviewers for their helpful comments. Chun Guo was partly supported by the National Natural Science Foundation of China (Grant No. 62002202).

Author information

Authors and Affiliations

  1. Key Laboratory of Cryptologic Technology and Information Security of Ministry of Education, Shandong University, Qingdao, Shandong, 266237, China

    Shanjie Xu, Qi Da & Chun Guo

  2. School of Cyber Science and Technology, Shandong University, Qingdao, Shandong, China

    Shanjie Xu, Qi Da & Chun Guo

  3. Shandong Research Institute of Industrial Technology, Jinan, Shandong, China

    Chun Guo

Authors
  1. Shanjie Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Qi Da
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chun Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chun Guo .

Editor information

Editors and Affiliations

  1. University of Hyogo, Hyogo, Japan

    Takanori Isobe

  2. Indian Institute of Technology Madras, Chennai, India

    Santanu Sarkar

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Xu, S., Da, Q., Guo, C. (2022). Minimizing Even-Mansour Ciphers for Sequential Indifferentiability (Without Key Schedules). In: Isobe, T., Sarkar, S. (eds) Progress in Cryptology – INDOCRYPT 2022. INDOCRYPT 2022. Lecture Notes in Computer Science, vol 13774. Springer, Cham. https://doi.org/10.1007/978-3-031-22912-1_6

Download citation

  • DOI: https://doi.org/10.1007/978-3-031-22912-1_6

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-031-22911-4

  • Online ISBN: 978-3-031-22912-1

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics