Skip to main content
SpringerLink
Log in

One-Against-All Halfplane Dichotomies

  • Conference paper
  • First Online:
Structural, Syntactic, and Statistical Pattern Recognition (S+SSPR 2022)

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 13813))

  • 398 Accesses

Abstract

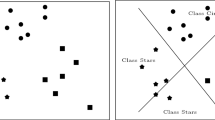
Given M vectors in N-dimensional attribute space, it is much easier to find M hyperplanes that separate each of the vectors from all the others than to solve M arbitrary linear dichotomies with approximately equal class memberships. An explanation of the rapid growth with M and N of the number of separable one-against-all linear halfplane dichotomies is proposed in terms of convex polyhedra in a hyperspherical shell. The counterintuitive surge is illustrated by averaged results on pseudo-random integer arrays obtained by Linear Programming and Neural Networks. Although the initial motivation arose from seemingly arbitrary rankings of scientists and universities, this project is not directed at any application.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 89.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 119.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

References

  1. Nagy, G., Krishnamoorthy, M.: MeFirst ranking and multiple dichotomies via linear programming and neural networks. In: ICPR 2022 (2022). Accepted

    Google Scholar 

  2. Duda, R.O., Hart, P.E., Stork, D.G.: Pattern Classification. Wiley, New York (2001)

    MATH  Google Scholar 

  3. Fukunaga, K.: Statistical Pattern Recognition, 2nd edn. Academic Press, Cambridge (1990)

    MATH  Google Scholar 

  4. Theodoridis, S., Koutroumbas, K.: Pattern Recognition. Academic Press, Cambridge (2009)

    Google Scholar 

  5. Bishop, C.M.: Pattern Recognition and Machine Learning. Springer, New York (2006). ISBN 978-0387-31073-2

    Google Scholar 

  6. Li, F.-F., Fergus, R., Perona, P.: One-shot learning of object categories. IEEE Trans. Pattern Anal. Mach. Intell. 28(4), 594–611 (2006)

    Article  Google Scholar 

  7. Nilsson, N.J.: Learning Machines: The Foundations of Trainable Pattern-Classifying Systems. McGraw-Hill, New York (1965)

    MATH  Google Scholar 

  8. Hughes, G.F.: On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory IT 4(1), 55–63 (1968)

    Article  Google Scholar 

  9. Hilbert, D., Cohn-Vossen, S.: Geometry and the Imagination, Chap. III. Chelsea Publishing, Hartford (1952)

    Google Scholar 

  10. Coxeter, H.S.M.: Introduction to Geometry, Chap. 22. Wiley, Hoboken (1989)

    Google Scholar 

  11. Woldfram MathWorld, Hypersphere. https://mathworld.wolfram.com/Hypersphere.html

  12. Shawe-Taylor, J., Cristianini, N.: Kernel Methods for Pattern Analysis. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  13. Dantzig, G.B.: Maximization of a linear function of variables subject to linear inequalities. In: Koopmans, T.C. (ed.) Activity Analysis of Production and Allocation. Wiley & Chapman-Hall (1951)

    Google Scholar 

  14. Gass, S.L.: Linear Programming, 5th edn. Dover, Downers Grove (2003)

    Google Scholar 

  15. Karmarkar, N.: A new polynomial-time algorithm for linear programming. In: Proceedings of the Sixteenth Annual ACM Symposium on Theory of Computing, STOC 1984, p. 302 (1984)

    Google Scholar 

  16. Nabli, H.: An overview on the simplex algorithm. Appl. Math. Comput. 210(2), 479–489 (2009)

    MathSciNet  MATH  Google Scholar 

  17. Rosenblatt, F.: The perceptron: a probabilistic model for information storage and organization in the brain. Psychol. Rev. 65, 386 (1958)

    Article  Google Scholar 

  18. Rosenblatt, F.: Principles of Neurodynamics. Spartan Books, New York (1962)

    MATH  Google Scholar 

  19. Barker, T.: A Computer Program for Simulation of Perceptrons and Similar Neural Networks: User’s Manual. CSRP Report #8. Cornell University, Ithaca, NY (1966)

    Google Scholar 

  20. MATLAB: Deep Learning Toolbox. https://www.mathworks.com/products/deep-learning.html. Accessed 12 Jan 2021

  21. Muller, J.Z.: The Tyranny of Metrics. Princeton University Press, Princeton (2018)

    Book  Google Scholar 

  22. Biangioli, M., Lippman, A.: Gaming the Metrics. MIT Press, Cambridge (2020)

    Book  Google Scholar 

  23. Johnson, S.: The Writing on the Wall, The New York Times Magazine, 17 April 2022 (2022)

    Google Scholar 

  24. Ioannidis, J.P.A., Boyack, K.W., Baas, J.: Updated science-wide author databases of standardized citation indicators. PLoS Biol. 18(10), e3000918 (2020). https://doi.org/10.1371/journal.pbio.3000918

    Article  Google Scholar 

  25. Mendelay: Data for “Updated science-wide author databases of standardized citation indicators”. https://data.mendeley.com/datasets/btchxktzyw/2. Accessed 10 Apr 2021

  26. QS World University Ratings. https://group.intesasanpaolo.com/content/dam/portalgroup/nuove-immagini/sociale/2022_QS_World_University_Rankings_1.pdf. Accessed 30 Nov 2021

Download references

Author information

Authors and Affiliations

  1. Rensselaer Polytechnic Institute, Troy, N.Y., 12180, USA

    George Nagy & Mukkai Krishnamoorthy

Authors
  1. George Nagy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mukkai Krishnamoorthy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to George Nagy .

Editor information

Editors and Affiliations

  1. Concordia University, Montreal, QC, Canada

    Adam Krzyzak

  2. Concordia University, Montreal, QC, Canada

    Ching Y. Suen

  3. Ca Foscari University of Venice, Venezia, Italy

    Andrea Torsello

  4. Concordia University, Montreal, QC, Canada

    Nicola Nobile

Rights and permissions

Reprints and permissions

Copyright information

© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Nagy, G., Krishnamoorthy, M. (2022). One-Against-All Halfplane Dichotomies. In: Krzyzak, A., Suen, C.Y., Torsello, A., Nobile, N. (eds) Structural, Syntactic, and Statistical Pattern Recognition. S+SSPR 2022. Lecture Notes in Computer Science, vol 13813. Springer, Cham. https://doi.org/10.1007/978-3-031-23028-8_19

Download citation

  • DOI: https://doi.org/10.1007/978-3-031-23028-8_19

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-031-23027-1

  • Online ISBN: 978-3-031-23028-8

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics

Search

Navigation