Abstract
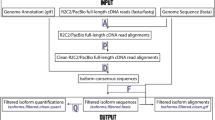
Long-read sequencing technologies demonstrate high potential for de novo discovery of complex transcript isoforms, but high error rates pose a significant challenge. Existing error correction methods rely on clustering reads based on isoform-level alignment and cannot be efficiently scaled. We propose a new method, I-CONVEX, that performs fast, alignment-free isoform clustering with almost linear computational complexity, and leads to better consensus accuracy on simulated, synthetic, and real datasets.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Steijger, T., et al.: Assessment of transcript reconstruction methods for RNA-seq. Nat. Meth. 10, 1177–1184 (2013)
Kannan, S., Hui, J., Mazooji, K., Pachter, L., Tse, D.: Shannon: an information-optimal de Novo RNA-Seq assembler. Preprint at https://www.biorxiv.org/content/10.1101/039230v1 (2016)
Mortazavi, A., Williams, B.A., McCue, K., Schaeffer, L., Wold, B.: Mapping and quantifying mammalian transcriptomes by RNA-Seq. Nat. Meth. 5, 621–628 (2008)
Wang, Z., Gerstein, M., Snyder, M.: RNA-Seq: a revolutionary tool for transcriptomics. Nat. Rev. Genet. 10, 57–63 (2009)
Gordon, S.P., et al.: Widespread polycistronic transcripts in fungi revealed by single-molecule mRNA sequencing. PLoS ONE 10, e0132628 (2015)
Wang, B., et al.: Unveiling the complexity of the maize transcriptome by single-molecule long-read sequencing. Nat. Commun. 7, 11708 (2016)
Hwang, B., Lee, J.H., Bang, D.: Single-cell RNA sequencing technologies and bioinformatics pipelines. Exp. Mol. Med. 50, 96 (2018)
Sahlin, K., Tomaszkiewicz, M., Makova, K.D., Medvedev, P.: Deciphering highly similar multigene family transcripts from Iso-Seq data with IsoCon. Nat. Commun. 9, 4601 (2018)
Abdel-Ghany, S.E., et al.: A survey of the sorghum transcriptome using single-molecule long reads. Nat. Commun. 7, 11706 (2016)
Weirather, J.L., et al.: Characterization of fusion genes and the significantly expressed fusion isoforms in breast cancer by hybrid sequencing. Nucleic Acids Res. 43, e116 (2015)
Westbrook, C.J., et al.: No assembly required: full-length MHC class I allele discovery by PacBio circular consensus sequencing. Hum. Immunol. 76, 891–896 (2015)
Roberts, A., Pachter, L.: Streaming fragment assignment for real-time analysis of sequencing experiments. Nat. Meth. 10, 71–73 (2013)
Trapnell, C., et al.: Transcript assembly and quantification by RNA-Seq reveals unannotated transcripts and isoform switching during cell differentiation. Nat. Biotechnol. 28, 511–515 (2010)
Broder, A.Z.: On the resemblance and containment of documents. Compression Complex. Seq. 1997, 21–29 (1997)
Ondov, B.D., et al.: Mash: fast genome and metagenome distance estimation using MinHash. Genome Biol. 17, 1–14 (2016)
Berlin, K., et al.: Assembling large genomes with single-molecule sequencing and locality-sensitive hashing. Nat. Biotechnol. 33, 623–630 (2015)
Gionis, A., Indyk, P., Motwani, R.: Similarity search in high dimensions via hashing. In: VLDB, vol. 99, no. 6 (1999)
Tardaguila, M., et al.: SQANTI: extensive characterization of long-read transcript sequences for quality control in full-length transcriptome identification and quantification. Genome Res. 28, 396–411 (2016)
Safonova, Y., et al.: IgRepertoireConstructor: a novel algorithm for antibody repertoire construction and immunoproteogenomics analysis. Bioinformatics 31, i53–i61 (2015)
Gibrat, J.F.: A short note on dynamic programming in a band. BMC Bioinf. 19(1), 1–5 (2018)
Clauset, A., Newman, M.E.J., Moore, C.: Finding community structure in very large networks. Phy. Rev. E 70, 066111 (2004)
Tseng, E., Tang, H., AlOlaby, R.R., Hickey, L., Tassone, F.: Altered expression of the FMR1 splicing variants landscape in premutation carriers. Biochim. Biophys. Acta 1860, 1117–1126 (2017)
Steeb, W., Hardy, Y.: Matrix Calculus and Kronecker Product: A Practical Approach to Linear and Multilinear Algebra, 2nd edn. World Scientific Publishing Company, Singapore (2011
Bertsekas, D.P.: Nonlinear programming. J. Oper. Res. Soc. 48, 334 (1997)
Tibshirani, R.: Regression shrinkage and selection via the lasso. J. R Stat. Soc. Ser. B Methodol. 58, 267–288 (1996)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix
1.1 Supplementary Note 1: Identifiability of de novo Transcriptome Recovery from Long Reads
A family of distributions \(P = \{{P}_{\theta }| \theta \in \Theta \}\) parameterized by a vector \(\theta \) is called identifiable if it satisfies the following condition:
This means that with enough observations from one of the distributions inside the family, one can decide which \(\theta \) is the ground-truth value. For the de novo transcriptome recovery problem, \(\theta \) is defined as the set of unknown transcripts/sequences \(S = \{{s}_{1}, {s}_{2}, ..., {s}_{m}\}\) and their corresponding abundances \(\rho = \{{\rho }_{1}, {\rho }_{2}, ..., {\rho }_{m}\}\). For a given read\(r\), we define \({P}_{\theta }(r)\) as the probability of observing \(r\), given \(\theta = (S, \rho ).\) We assume that a read generated from a sequence by adding insertion, deletion, or substitution errors through an i.i.d. process which does not depend on the location of the error. For simplicity, let \({\delta }_{s}, {\delta }_{i},\) and \({\delta }_{d}\) be the probability of observing a substitution, insertion, or deletion error at each location of the sequence respectively. In Theorem 1, we prove that the problem of de novo transcriptome recovery is identifiable.
Supplementary Theorem 1 (Long-Read Sequencing Identifiability):
Assume that the set of sequences \(S = \{{s}_{1}, {s}_{2}, ..., {s}_{m}\}\) with the corresponding abundances \(\rho = \{{\rho }_{1}, {\rho }_{2}, ..., {\rho }_{m}\}\) is unknown. Suppose that for any read\(r\), \({P}_{S, \rho }(r)\) represents the probability of observing read \(r\) given that it is generated from a sequence in \(S\) with the abundance vector\(\rho \). Then, given \({P}_{S, \rho }(r)\) for all reads\(r\), both \(S\) and \(\rho \) can be exactly recovered when substitution error parameter\({\delta }_{s} \ne \frac{3}{4}\).
Proof:
Each read \(r\) with non-zero \(P(r)\) can be obtained by adding insertions, deletions, and substitutions to one or several sequences in \(S\). Without loss of generality, we can model the transcriptome recovery problem as denoising the reads obtained by applying three noise channels to the set of sequences in \(S\) sequentially (Supplementary Figure 1). In this model, \({P}_{1}(r)\) is the distribution of reads after the substitution channel; and \({P}_{2}(r)\) is the distribution of reads after applying the deletion channel (and before the insertion channel). Lastly, \(P(r)\) is the final probability distribution observed after applying the insertion noise. If we prove that the transcriptome recovery is identifiable under each one of these three channels (insertion, deletion, and substitution) individually, then the entire problem is identifiable. This is because of the fact that using the given probability of observing reads \(P(r)\), we can recover \({P}_{2}(r)\) by denoising the effect of the insertion channel. Then, with the same argument, we can recover \({P}_{1}(r)\) by denoising the effect of the deletion channel. Finally, we can find the vector \(\rho \) by denoising the effect of the substitution channel on the probability vector \({P}_{1}\). Thus, it suffices to show that \({P}_{2}(r), {P}_{1}(r),\) and \(\rho \) can be recovered sequentially given \(P(r)\). In what follows, we show each one of these three channels is identifiable.
Identifiability Under the Substitution Channel:
For the substitution channel, we can observe that a read \(r\) with length \(L\) can only be generated from a sequence of size \(L\), since the substitution does not change the sequence length. Thus, for estimating the abundances of the sequence with size \(L\), we can only focus on the set of reads with size \(L\). It means that without loss of generality we can assume that the set of reads and sequences are all of size \(L\). Moreover, without loss of generality, assume that S consists of all \({4}^{L}\) possible transcripts with size \(L\) with possibly zero abundances. Thus, the problem is reduced to recovering vector \(\rho \), given the \(P(r)\) and \(S\). Let \({\delta }_{s}=\delta \) be the substitution error rate. Then the probability of observing the read \({r}_{i}\) can be written as follows:
Here \(d({r}_{i},{s}_{j})\) is the number of mismatches between \({r}_{i}\) and \({s}_{j}\). This relationship can be written in a matrix form. For example, when \(L=1\), let the abundances of ‘A’, ‘C’, ‘G’, and ‘T’ be \({\rho }_{1}, {\rho }_{2}, {\rho }_{3}\) and \({\rho }_{4}\) respectively. Then, the probability of observing each {‘A’, ‘C’, ‘G’, ‘T’} can be obtained by the following equation:
where
Thus, the identifiability problem in this case reduces to showing the invertibility of this matrix. Notice that the determinant of this matrix can be computed as

where the second equality is due to the effect of permuting rows on the determinant of the matrix. One can easily check that this polynomial is non-zero for all \(\delta \in [0, 1]\) except \(\delta = \frac{3}{4}\), which implies the invertibility of the matrix for all \(\delta \in [0, 1]\) except \(\delta = \frac{3}{4}\).
Now, let us consider the case of general length \(L>1\). Assume that we order the set of all possible sequences with size \(L\) (all \(m={4}^{L}\) possible sequences) according to the order of sequences in base \(4\). In this case, the probability transition relation can be written as
where the Kronecker product of two matrices \({A}_{(m \times n)}\) and \({B}_{(p \times q)}\) is a matrix \({C}_{((m\times p) \times (n\times q))}\), defined as:
The Kronecker product of \(L\) matrices is invertible if and only if each one of them is invertible [23]. We have already shown that \(A\) is an invertible matrix when \({\delta }_{s}\ne \frac{3}{4}\). Thus, \(A \otimes A\otimes ... \otimes A\) is invertible as well, which shows the problem is identifiable when the substitution channel is applied.
Insertion Channel:
Let \(R\) be the support of \(P\) (\(R = \{r: P(r) > 0\}\)). We define the operator \(\le \) on a pair of reads as follows: \({r}_{1 }\le {r}_{2}\) if \({r}_{2}\) can be obtained by inserting zero or more bases to \({r}_{1}\) in different locations. It is easy to observe that \((R, \le )\) forms a partially ordered set (poset). Since it satisfies the reflexivity, anti-symmetry, and transitivity. We have the following observations:
-
If \(r^{\prime} \le r\) and \(r \ne r^{\prime}\), then \(\left| {r^{\prime}} \right| < \left| r \right|\).
-
R has at least one minimal element.
-
Any minimal element of \(R\) belongs to \(S\).
To see the correctness of the first observation, assume that \(r^{\prime} \le r\), which means r is obtained by adding zero or more characters to r. However, since \(r^{\prime} \ne r\), the number of added characters cannot be zero. Thus at least one character is added to \(r^{\prime}\) to obtain r. This means that \(\left| {r^{\prime}} \right| \le \left| r \right|\).
To prove the second observation, assume that \(r_{min}\) is an element of \(R\) with the minimum length (it is not necessarily unique). Indeed, such an element exists, because \(\left| r \right| \ge 1\) for all \(r \in R\). We claim that \(r_{min}\) is a minimal element. We prove by contradiction. Assume that \(r_{min}\) is not a minimal element. Thus, there exists an element \(r^{\prime} \ne r_{min}\) in \(R\) such that \(r^{\prime} \le r_{min}\). According to the first observation \(\left| r \right| < \left| {r_{min} } \right|\), which contradicts the fact that \(r_{min}\) is an element with the minimum length in \(R\).
Finally, we prove that a minimal element of \(R\) belongs to \(S\). We prove by contradiction. Assume that \({r}_{min}\) is a minimal element that does not belong to \(S\). Thus, there exists an element \(s\in S\), such that \(s \le {r}_{min}.\) Clearly \(r=s\) belongs to \(R\), since \(P(r)\ge P(r|s)={\rho }_{s}(1 - {\delta }_{i}{)}^{|s|}>0\). Therefore, \(s\) is an element in \(R\) which is not equal to \({r}_{min}\) and \(s\le {r}_{min}\) which contradicts with the fact that \({r}_{min}\) is a minimal element in \(R.\)
Now, we prove the identifiability of the transcriptome recovery problem under the insertion channel by induction on the size of \(S\).
For \(|S|=1\), according to the third observation, the minimal member of \(R\) belongs to \(S\), and its abundance is clearly \(1\).
Based on the induction hypothesis, assume that the problem is identifiable when \(|S|=m\). We want to prove it is identifiable, when \(|S|=m+1\). Based on the third observation, any minimal element \({r}_{min}\) of \(R\) belongs to \(S\). Set \(S^{\prime} = S - \left\{ {r_{min} } \right\}\) and update the probability vector of the reads accordingly: \(P^{\prime}\left( r \right) = P\left( r \right) - P(r|r_{min} )\rho_{{r_{min} }}\). For updating the probability vector of reads we need to estimate \({\rho }_{{r}_{min}}\) exactly. Since \({r}_{min}\) is the minimal element, it can be only obtained from a sequence with the exact same structure. Hence, \(P({r}_{min}) = {\rho }_{{r}_{min}}(1-\delta {)}^{|{r}_{min}|}\), which means \({\rho }_{{r}_{min}}=\frac{P({r}_{min})}{(1-\delta {)}^{|{r}_{min}|}}.\) According to the assumption of induction, since \(\left| {S^{\prime}} \right| = m\). we can recover \(S^{\prime}\) using \(P^{\prime}\). Thus, \(S = S^{\prime} \cup \left\{ {r_{min} } \right\}\), which means we can recover \(S\) exactly.
Deletion Channel:
The argument is similar to the insertion channel. The only difference is that the operator \(\le \) is defined for a pair of reads \({r}_{1 }\le {r}_{2}\) if \({r}_{2}\) can be obtained by deleting some elements of \({r}_{1}\). Moreover, the minimal element of \(R\) is the longest read in this case.
1.2 Supplementary Note 2: Sparse EM Algorithm Inside the Isoform Recovery via Convexification
As discussed in Sect. 3, the maximum likelihood estimator of the abundance vector given the set of transcripts and reads can be written as:
Or equivalently:
Applying the Expectation Maximization (EM) algorithm, at each iteration, we minimize a tight local upper bound of the above objective function:
The Lagrangian function of the above problem can be written as:
And the dual problem takes the form of:
Since the Lagrangian function is convex in \(\rho \), and the constraints are linear, the strong duality holds [24]. Thus, by setting the gradient of \(L\) with respect to \(\rho \) to 0, we have:
Which means:
Since \(\sum\nolimits_{j=1}^{m}{{\rho }_{j}^{t+1}}= 1\), we have:
Therefore \({\lambda }^{*}= n\), and
This update rule is similar to the one used by Express [12] to obtain the abundance vector.
Sparsification.
One naïve approach to impose sparsity to the estimated abundances in the above problem is to use the \( \ell _{1} \) regularizer [25]. However, the abundances are non-negative and their summation is equal to \(1\). Therefore, the \(\ell _{1} \) regularizer does not change the objective function at all. Thus, instead of using \(\ell _{1}\) regularizer, we apply the \(\ell{l}q\) regularizer to the objective function with \(0< q < 1\). Using this regularizer, the above problem can be written as
Thus, the Lagrangian function for the sparse EM takes the following form:
Again, by writing the optimality condition for the dual problem, we have
Moreover, according to the complementary slackness, we have:
It is easy to observe that \({\lambda }^{*}\ne 0\), otherwise the last two equalities have no solution. Thus, similar to the previous case, we can conclude that \({\lambda }^{*}=n\), and we have the following closed-form update rule:
We refer to \(\frac{1}{q}\) as the sparsity power. This hyper-parameter is set to \(1.03\) in the implementation of Isoform Recovery via Convexification module. As we increase the sparsity power, the abundance vector is sparser, and thus the number of recovered isoforms is smaller at the end. Sparsification of EM can help to remove false positive isoforms further. However, we should avoid setting it to very large numbers as it may lead to the removal of true positives.
1.3 Supplementary Note 3: Further Analysis of MinHash and Locality Sensitive Hashing Algorithms
Definition 1:
Suppose that \({S}_{1}\) and \({S}_{2}\) are k-mer sets of two given sequences. The Jaccard similarity of \({S}_{1}\) and \({S}_{2}\) is defined as
Definition 2:
Given a set of sequences \({S}_{1},\dots ,{S}_{m}\) and the set of k-mers \(S^{\prime}_{1} , \ldots ,S^{\prime}_{{N^{\prime}}}\), we say a matrix \(M \in \left\{ {0,1} \right\}^{{N^{\prime} \times m}}\) is a representation matrix if it satisfies the following property: The element in row \(i\) and column \(j\) equals \(1\) if and only if the i-th k-mer appears in j-th sequence, and \(0\) otherwise.
Definition 3:
Assume the representation matrix \(M\) has \(N^{\prime}\) rows and \(m\) columns, and let \({\mathcal{P}} = \left\{ {i_{1} ,i_{2} , \ldots ,i_{{N^{\prime}}} } \right\}\) be a permutation of set \(\left\{ {1,2, \ldots ,N^{\prime}} \right\}\), and column \(c\) in \(M\) corresponds to a sequence \(S\). Then the MinHash signature of \(S\) with respect to \(\mathcal{P}\) is defined as \({\mathrm{MinHash}}_{\mathcal{P}}(c)={i}_{j}\) where \(j\) is the smallest number in \(\left\{ {1,2, \ldots ,N^{\prime}} \right\}\) such that \(M[{i}_{j}][c]=1\).
Example:
Assume that \({S}_{1}={\text{ACCAGTC}}\) and \({S}_{2}={\text{ACCGTCA}}\). The set of 3-mers that appears at least once in \({S}_{1}\) or \({S}_{2}\) is \(\{\mathrm{ACC},\mathrm{ CCA},\mathrm{ CAG},\mathrm{ AGT},\mathrm{ GTC},\mathrm{ CCG},\mathrm{ CGT},\mathrm{ TCA}\}.\) Let \(\mathcal{P}=\{7, 5, 2, \mathrm{3,1},\mathrm{4,6}\}\) be a random permutation of 3-mer indices. Since \(5\) is the first 3-mer index in \(\mathcal{P}\) such that its corresponding 3-mer appears in \({S}_{1}\), thus, the MinHash signature of \({S}_{1}\) with respect to \(\mathcal{P}\) is \(5\). With the same logic, we can observe that the MinHash signature of \({S}_{2}\) with respect to \(\mathcal{P}\) is \(7\).
Supplementary Theorem 2:
Let \(J\left({S}_{1},{S}_{2}\right)\) be the Jaccard similarity between two given sequences \({S}_{1}\) and \({S}_{2}\), and \({\mathcal{P}}_{1},\dots ,{\mathcal{P}}_{h}\) are \(h\) distinct randomly generated permutations of set \(\{\mathrm{1,2},\dots ,{N}^{^{\prime}}\}\). For each sequence, a vector of MinHash signatures with length \(h\) is computed with respect to permutations \({\mathcal{P}}_{1},\dots ,{\mathcal{P}}_{h}\). Then, \(\frac{{\# {\text{Matches}}\;{\text{between}}\;{\text{signature}}\;{\text{vectors}}\;{\text{of}}\;S_{1} \;{\text{and}}\;S_{2} }}{h}\) is an unbiased estimator of the Jaccard similarity of \({S}_{1}\) and \({S}_{2}\).
Proof:
Let \({c}_{1}\) and \({c}_{2}\) be the indices of columns in \(M\) corresponding to \({S}_{1}\) and \({S}_{2}\). Let \({R}_{1}\) denote the set of rows in which \({c}_{1}\) and \({c}_{2}\) both have the value \(1\), and \({R}_{2}\) be the set of rows in which exactly one of \({c}_{1}\) and \({c}_{2}\) is \(1\). Fix a permutation \(\mathcal{P}={\{i}_{1},{i}_{2},\dots ,{i}_{{N}^{^{\prime}}}\}\), and let \(j\) be the smallest index such that at least one of \(M\left[{i}_{j}\right]\left[{c}_{1}\right]\) or \(M\left[{i}_{j}\right]\left[{c}_{2}\right]\) is \(1\). Thus \({i}_{j }\in {R}_{1}\cup {R}_{2}\). Moreover, \({\mathrm{MinHash}}_{\mathcal{P}}\left({\mathrm{c}}_{1}\right)={\mathrm{MinHash}}_{\mathcal{P}}\left({\mathrm{c}}_{2}\right)={i}_{j}\) if and only if \({i}_{j} \in {R}_{1}\). Hence \(Pr[{\mathrm{MinHash}}_{\mathcal{P}}\left({\mathrm{c}}_{1}\right)={\mathrm{MinHash}}_{\mathcal{P}}\left({\mathrm{c}}_{2}\right)] = \frac{|{R}_{1}|}{{|{R}_{1}|+|R}_{2}|}\) which is equal to the Jaccard similarity of \({S}_{1}\) and \({S}_{2}\). Thus, we have
which means the estimator is unbiased.
Supplementary Theorem 3:
The variance of the estimator proposed in Theorem 2 is equal to \(\frac{J({S}_{1}, {S}_{2}) - {J}^{2}({S}_{1}, {S}_{2})}{h}\).
Proof:
Since the probability of match between two MinHash signatures for each permutation \({\mathcal{P}}_{k}\) equals to \(J({S}_{1}, {S}_{2})\), thus \(\#\mathrm{Matches\ between\ signature\ vectors\ of}\ {S}_{1}\ \mathrm{and}\ {S}_{2}\) follows a binomial distribution with \(h\) trials (number of permutations) and \(p = J({S}_{1}, {S}_{2})\). Thus its variance equals \(hp(1-p)\). Therefore,
To obtain the MinHash signatures of reads in a given dataset, we need \(O(NL)\) operations to form k-mer set of sequences, and \(O(hNL)\) operations to obtain MinHash signatures of reads, where \(N\) is the number of reads, \(L\) is the average length of the sequences, and \(h\) is the length of MinHash signatures.
Choosing the Hyper-parameters of the Locality Sensitive Hashing Algorithm
Hashing the reads using MinHash reduces the computational complexity of comparison significantly, since comparing the MinHash signature of two given reads needs \(O\left(h\right)\), while computing the edit distance of two reads requires \(O\left({L}^{2}\right)\) operations (\(L\) can be varied from \(400\) to \(10k\), while \(h\) can be selected as a constant number typically less than \(100\)). Still, comparing the MinHash signatures of all \(O\left({N}^{2}\right)\) pairs of sequences is inefficient for large-scale datasets consisting of millions of sequences. LSH algorithm copes with this issue by dividing the \(h\) entries of the MinHash signature into \(b\) bands of size \(d\) \((h\boldsymbol{ }=\boldsymbol{ }bd)\). If two sequences are equal in all rows of at least one of the bands, they are considered as a candidate similar pair. For the default hyper-parameters of I-CONVEX \((d=1, b=10, k=15)\) the probability of considering two sequences as similar for different values of their Jaccard similarity is depicted in Supplementary Figure 2. We have selected the default values of hyper-parameters such that the probability of having a false negative is small. However, this leads to a higher rate of false positives as well. As we mentioned in Sect. 3, we validate the obtained candidate pairs by a designed convolutional neural network to remove the false positive edges in our similarity graph.
1.4 Supplementary Note 4: Architecture of Convolutional Neural Network
To validate the similarity of candidate pair obtained from Locality Sensitive Hashing Algorithm we trained a convolutional neural network with the training data described in Results section. In this supplementary, we explain the architecture of the convolutional neural network.
Architecture.
To train the convolutional neural network that validates the similarity of candidate pairs, for each pair in the generated training dataset (which can be similar or dissimilar), both reads are one-hot encoded first (Each letter corresponds to a \(4\times 1\) array). Since the length of each read in the generated dataset is 400, we obtain two arrays of size \(4\times 400\) after one-hot encoding of the reads. Then, we concatenate these two arrays row-wise to obtain an \(8\times 400\) array. These \(8\times 400\) arrays are the input data to the convolutional neural network with the layers depicted in Table 1.
The final value after passing each \(8\times 400\) input from the convolutional neural network is a scalar representing the predicted value. This scalar ranges between \(-1\) and \(1\), representing the similarity of a given pair. To compute the loss, let \({y}_{i}\) and \({\widehat{y}}_{i}\) be the predicted value, and the true label corresponding to the i-th candidate pair. We use \({\ell{l}}_{2}\) loss defined as follows:
To optimize the weight parameters in the network, an Adam optimizer is applied to the \({\ell{l}}_{2}\) loss.
Validation of Candidate Similar Pairs:
To validate a given candidate similar pair by the trained convolutional neural network, first each read is trimmed to a sequence with length \(400\) (if the length of a read is less than\(400\), we add enough base ‘A’ to the end of the sequence to reach the length of\(400\)). Each one of the two trimmed reads is one-hot encoded to get an array of size \(4\times 400\). By concatenating them, an array with the size \(8\times 400\) is obtained. Then, it will be passed through the convolutional neural network, and it gives a number within the range of \([-1, +1]\). If the number is greater than\(0\), we consider them as a similar pair.
1.5 Supplementary Note 5: I-CONVEX Pipeline
To run I-CONVEX on a given genome reads dataset, first move the fasta file to the Clustering folder and rename it to reads.fasta. Then execute the following commands in order to obtain pre-clusters:

The result is a Cluster folder containing subfolders, each of which represents a pre-cluster. Now, the following commands run the clustering via convexification module on pre-clusters:

The last command stores the final collected transcripts on the final_transcripts.fasta file.
To run all parts of the algorithm step by step, or change the hyper-parameters such as \(k\), \(d\), and \(b\), follow the advanced version instructions on https://github.com/sinaBaharlouei/I-CONVEX.
Supplementary Figures: Distribution of Sequence Lengths in Synthetic and Real Datasets
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Baharlouei, S., Razaviyayn, M., Tseng, E., Tse, D. (2023). I-CONVEX: Fast and Accurate de Novo Transcriptome Recovery from Long Reads. In: Koprinska, I., et al. Machine Learning and Principles and Practice of Knowledge Discovery in Databases. ECML PKDD 2022. Communications in Computer and Information Science, vol 1753. Springer, Cham. https://doi.org/10.1007/978-3-031-23633-4_23
Download citation
DOI: https://doi.org/10.1007/978-3-031-23633-4_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-23632-7
Online ISBN: 978-3-031-23633-4
eBook Packages: Computer ScienceComputer Science (R0)