Obstacles on the Pathway Towards Chemical Programmability Using Agglomerations of Droplets

Abstract

We aim at planning and creating specific agglomerations of droplets to study synergic communication using these as programmable units. In this paper, we give an overview of preliminary obstacles for the various research issues, namely of how to create droplets, how to set up droplet agglomerations using DNA technology, how to prepare them for confocal microscopy, how to make a computer see droplets on photos, how to analyze networks of droplets, how to perform simulations mimicking experiments, and how to plan specific agglomerations of droplets.

This work has been partially financially supported by the European Horizon 2020 project ACDC – Artificial Cells with Distributed Cores to Decipher Protein Function under project number 824060.

1 Introduction

Usually, when writing a paper one starts off with describing the problem one considers, how it is embedded in a whole class of problems, why it is of importance, and cites own preliminary work and the related papers of others in this field. Then one describes the problem in a more detailed way and also the approach one intends to use on this problem. Afterwards one presents results achieved with this approach and rounds the paper off with a summary of the results and an outlook on future work. In this way, this paper is highly unusual, as we present a list of obstacles on the pathway to what we intend to do. This list is most probably even not complete, these are only the problems we have become aware of in recent years. We have made progress with all of them but are still far from solving many of them in the way we intend.

Within the context of the EU Horizon project ACDC (Artificial Cells with Distributed Cores to Decipher Protein Function), we aim at developing a chemical compiler [4, 27]. This device should be able to e.g. produce some desired macromolecules on demand, especially for medical purposes. It contains a large variety of chemical educts, which are filled in droplets of various sizes. The task is to create a specific agglomeration of some of these droplets. They should then exchange chemicals in a controlled way via pores in the bilayers formed during the agglomeration process, thus allowing a gradual chemical reaction scheme, which then efficiently produces the desired macromolecule.

In order to get to the point where we can design an experiment leading to a desired agglomeration of droplets, we need to know

• how to best create droplets of specific sizes,

• how this agglomeration process works

  • by setting up various experiments leading to an agglomeration of droplets,

  • by taking pictures during and after the agglomeration process,

  • by analyzing these pictures on a computer,

  • by analyzing the networks of droplets within the agglomerations,

  • and then by iteratively changing experimental parameters and analyzing the resulting changes in the networks,

• what the physical laws governing the agglomeration process are

  • by modelling the agglomeration process [20],

  • by simulating this model on a computer [22], mimicking an experiment,

  • by analyzing the networks of droplets resulting in these simulations [20, 21],

  • by comparing these results with the corresponding outcomes from the experiments,

  • and then by iteratively changing the model in order to get closer to the experimental outcome,

• what specific agglomeration of droplets is needed for producing the desired macromolecule

  • by planning the gradual reaction scheme resulting in the desired macromolecule,

  • by planning the reaction network allowing this gradual reaction scheme,

  • by being aware of geometric and physical limitations to realize specific networks,

  • by embedding the network of droplets for the reaction process in an even larger agglomeration of droplets to physically stabilize the central reaction network if necessary,

  • and by designing the experiment leading to this specific agglomeration of droplets.

2 Setting Up the Experiment

2.1 Creating Droplets

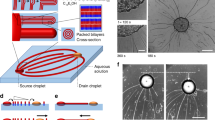
Different ways of creating droplets have their specific advantages and drawbacks. In the experiments performed in David Barrow’s group at Cardiff University, T-junctions are used in which a fluid stream inside another fluid is split in a sequence of droplets. With this microfluidic approach, it is necessary to determine the correct pressure ratio between the two fluids, such that the system is in a dripping and not a jetting or squeezing regime [10]. In the T-junction, the continuous phase (watery) fluid breaks the dispersed (oily) phase fluid, and consequently the dispersed phase fluid is sheared to form tiny droplets. This geometry is easy to fabricate and creates droplets of relatively high monodispersity at a high rate.

Another approach is used in experiments performed in Martin Hanczyc’s group at the University of Trento. Hereby a low-concentrated solution of phospholipids in oil, which is first sonicated for 15 min, is added to an aqueous hosting solution with low concentrations of glucose, sodium jodide, and Hepes. Some dodecane is added to avoid unwanted chloroform production and evaporation. As the density of the heavy oil used is larger than the density of water, the oil sinks through the water to the bottom of the phial. Then this mixture is emulsified by mechanical agitation, i.e., by shaking and repeatedly rubbing the phial over a vibrating board. While the droplets created in Cardiff exhibit almost the same radius value, this approach used in Trento leads to a polydisperse system of emulsion droplets surrounded by hulls of phospholipids with lognormally distributed radii [6].

2.2 Surface Functionalization and Self-assembly Process

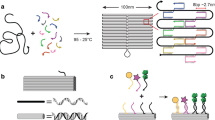
While the droplets in the experiments in Cardiff can immediately form more or less extended bilayers when touching each other, thus automatically starting an assembly process, the lipid surfaces of the droplets in Trento must be functionalized to allow connections with other droplets. For this purpose, streptavidin attached to a red or green fluorescent label and ssDNA oligonucleotides are diluted in the hosting solution and preincubated in the dark for 30 min at room temperature. (The sequences and the modifications of the ssDNA oligonucleotides are shown in [5].) Then this solution is mixed with the solution containing the droplets and incubated in the dark on a rocking at 40-60 rpm for roughly one hour, resulting in different droplet populations depending on streptavidin-DNA specific composition. Then the droplets are washed twice by centrifugation, by removing supernatant with vacuum, and replacing it with a fresh hosting solution. These functionalized droplets are then used immediately for the experiment. As shown in Fig. 1, the type of connections which can be formed by the droplets can be restricted and controlled by using complementary strands of DNA. Two droplet populations with different streptavidin colors are together incubated for two or three hours at room temperature in the dark and transferred afterward to a sealed microscopy observation chamber by gentle aspiration without resuspension.

Fig. 1.

Sketch of a pair of oil-filled droplets in water, to which complementary strands of ssDNA oligonucleotides are attached: The surfaces of the droplets are composed by single-tail surfactant molecules like lipids with a hydrophilic head on the outside and a hydrophobic tail on the inside, thus forming a boundary for the oil-in-water droplet. By adding some single-strand DNA to the surface of a droplet, it can be ensured that only desired connections to specific other droplets with just the complementary single-strand DNA can be formed. Please note that the connection of the droplets in this picture is overenlarged in relation to the size of the droplets. In reality, the droplets have a radius of 1–50 $\upmu {\text {m}}$, whereas a base pair of a nucleic acid is around $0.34\,\textrm{nm}$ in length [1], such that the sticks of connecting DNA strands are roughly 5 nm long.

2.3 Taking Pictures

Before pictures can be taken, the microscope slides are prewashed sequentially with acetone and ethanol and are dried with compressed air. Then they are covered with imaging spacers. The microscope chamber is preloaded with a mixture of the aqueous solution and some sample of the agglomeration. Finally, the observation chamber is effectively sealed with a prewashed coverslip. The samples at the end-point are evaluated using spinning disk confocal microscopy, as shown in Fig. 2.

Fig. 2.

Left: Picture of an assembly taken with confocal microscopy. Additionally to the red and green “painted” droplets, a yellow dot lights up at each DNA connection between pairs of red and green droplets. Right: Small part of an agglomeration of a polydisperse system of red and green droplets. (Please note that some of the circumcircles of larger droplets are displayed diffuse.)

3 How to Make a Computer “See” Droplets

When getting a stack of pictures of an agglomeration of red and green droplets, one needs to derive the information about the locations of their midpoints, their radii, and the connections between them. Each picture contains a two-dimensional cut through the three-dimensional agglomeration, as shown in Fig. 2. While a human can easily discern these droplets, several steps are needed to derive the information about positions and radii of the droplets on a computer, on which each picture is usually comprised by a two-dimensional array of pixels.

3.1 Color Filtering

Each pixel contains a color information. Usually, the RGB color model is used, i.e., for each pixel, there is one value for red, one value for green, and one value for blue. For example, if one byte is used for each of these three colors, then we have values between 0 and 255 for each of them, and thus more than 16.7 million colors can be represented on a computer.

Fig. 3.

HSV color model: On the left, the cone of possible colors for various hue color angles H, saturations S, and darkness values V are shown. H can take values between $0^\circ$ and $360^\circ$, S and V between 0 and 100. The example of how to compose the color “navyblue” in this HSV color model is presented on the right. (pictures taken from wikipedia [29]) (Color figure online)

However, the problem is that most colors are mixed colors with large proportions of at least two color channels. Thus, when using the RGB color model for filtering colors on a picture like the one in Fig. 2, while hoping to get either red or green, in many cases one will get signals for both colors and one then has to check whether there is a more dominant value in the other channel. Thus, it is preferrable to work with another color model, in which the color is defined by one value only. An example for such a model is the HSV color model, in which the possible colors are also represented by three values. But the true color information is stored in the so-called hue color-angle H only, as shown in Fig. 3. The other two values are the saturation S and the darkness value V. Each color stored in a RGB color coding can also be represented in this HSV color model (and related models) and vice versa [29]. But in this model, the filtering process is much easier, as one has to apply a filter for a specific range of hue angles only, only keeping in mind that S and V should have appropriate values. After this filtering for either red or green, one has two black and white pictures, in which the white and grey pixels correspond to pixels of formerly one color angle range, while the pixels in other color angle ranges are represented in black now.

3.2 Detecting Edges

In the next step, one has to determine the boundaries of a droplet. As can be seen in Fig. 2, some droplets appear as boundary rings only, others are completely filled disks, but most droplets are shown with a more or less sharp ring and an interior with a smaller saturation and a larger darkness value of the same color. In order to determine the boundaries of a droplet, an edge detection algorithm has to be applied.

A simple example for edge detection (Please note that the word “edge” in this section describes a part of a boundary of an object, whereas we use the word edge as a connection between a pair of nodes when referring to networks otherwise in this paper.) is the Sobel operator [23, 30]. Let A be a matrix containing the pixels of a color filtered picture, i.e., A(i, j) only contains a value for the greytone of this pixel, e.g., a value between 0 and 255. Then one applies

$$\begin{aligned} G_x= \left( \begin{array}{rrr} 1 &{} 0 &{} -1 \\ 2 &{} 0 &{} -2 \\ 1 &{} 0 &{} -1 \\ \end{array}\right) * A \text{ and } G_y= \left( \begin{array}{rrr} 1 &{} 2 &{} 1 \\ 0 &{} 0 &{} 0 \\ -1 &{} -2 &{} -1 \\ \end{array}\right) * A . \end{aligned}$$

(1)

Thus, for a specific pixel (x, y), $G_x(x,y)$ stores the value $A(x-1,y-1)-A(x+1,y-1)+2A(x-1,y)-2A(x+1,y)+A(x-1,y+1)-A(x+1,y+1)$. The larger the absolute value of $G_x(x,y)$, the more pronounced in the transition from black to white or vice versa in x-direction. The $G_y$ operator analogously detects such transitions in the y-direction. They can be combined to $G=\sqrt{G_x^2 + G_y^2}$, thus considering transitions in both x- and y-direction.

Here the next difficulty occurs: one has to find a proper cutoff, i.e., an answer to the question which G(x, y) value is large enough to show the transition from the outside of a droplet to its boundary. Thus, one defines a matrix B with $B(x,y)=1$ if G(x, y) exceeds some threshold value and $B(x,y)=0$ otherwise. However, larger droplets are often bounded by a rather diffuse ring only, such that the corresponding G values are not large. Thus, when choosing a too large threshold value, one will miss out many droplets, whereas a too small value will lead to many concentric rings and also to ghost particles which are not there. More elaborate edge detection operators have been developed in recent years [15], like the weights (47, 162, 47) instead of (1, 2, 1) [30] or weighted sums over even more pixels, but one still faces the problem to manually determine appropriate threshold values.

3.3 Identifying Objects

So far, the computer only has a matrix B of true/false values whether a transition takes place at a specific pixel or not, but it does not know anything about droplets and enclosing rings yet. Using the Hough transform [3, 8], structures like lines or circles can be detected. This method can be most easily explained for the detection of lines, as shown in Fig. 4.

For other structures like circles, the Hough transform can also be applied in an altered way. In contrast to a line which can be described by a slope and a y-axis-section only, three parameters are needed for a circle, namely the coordinates $(x_m,y_m)$ for the midpoint and the radius r, such that a histogram over three dimensions has to be created. In order to focus the search for correct radii, the range of radius values is restricted a priori. Then one performs a loop over possible $x_m$ values with some stepwidth and within this loop, a further loop over possible radii r with some stepwidth, calculates in the innermost third loop over all pixels the possible corresponding $y_m$ values if $\vert x_{\textrm{pixel}}-x_m\vert \le r$ and increments the corresponding entries in the three-dimensional histogram. Alternatively, one can go through all triples of pixels, assume that they might lie on a circle, and derive its midpoint coordinates and radius from them, as three points are necessary to define a circle. The peaks in the histogram indicate the circles and contain the information about their midpoints and radii. However, like for the edge detection, one has also to find appropriate threshold values for detecting true circles, while keeping in mind that the peaks for the small circles need to be lower than those of larger circles. Due to the diffuse nature of many larger circles and also because of other problems, especially the huge number of ten-thousands of droplets in one picture, an approach trying to detect all droplets and to determine their midpoint coordinates and their radii simultaneously only with the described methods fails. Instead, a very elaborate algorithm to detect droplets in a successive way has to be developed with a commercial software [11].

Fig. 4.

(picture taken from wikipedia [28])

Detection of lines in a picture using the Hough transform: On the left side, an exemplary picture with two lines is shown. A line can be represented by its Hesse normal form as $r= x_{\textrm{pixel}} \cos \vartheta + y_{\textrm{pixel}} \sin \vartheta$, with r being the shortest distance from a point on the line to the origin and $\vartheta$ being the angle between the line connecting this closest point to the origin and the x-axis. If scanning the range of possible $\vartheta$ values with small steps, performing a loop over all pixels for each value of $\vartheta$, calculating the corresponding r value, and creating a histogram of $(\vartheta ,r)$ values as shown on the right, one finds two peaks in this example, one peak for each line. Thus, this method returns the information about these two lines.

So far, we have only considered the evaluation of one picture only. But as we are interested in three-dimensional structures, a whole stack of pictures is needed. At least two cuts through each droplet are necessary in order to determine its real radius value and a third one to exclude the error that data from two different droplets have been mixed up. Here further problems occur, as the droplets move between the taking of successive pictures in a picture stack and as the microscope automatically readjusts the brightness when taking a new picture.

4 How to Analyze Networks of Droplets

While these algorithms for edge detection and object identification work very well on drawings or pictures of technical devices, they are often unable to detect the boundaries of a face on a painting, and also for our case, we have severe difficulties as already mentioned. But let us now assume that we have finally mastered the problem of detecting all droplets properly. As a next step, we have to determine the network of droplets. Mathematically speaking, a network (sometimes called graph) is comprised of a set of nodes and a set of edges connecting pairs of nodes. A network can be represented by an adjacency matrix $\eta$ between pairs (i, j) of nodes with

$$\begin{aligned} \eta (i,j)=\left\{ \begin{array}{ll} 1 &{} \text{ if } \text{ an } \text{ edge } \text{ between } i \text{ and } j \text{ exists }\\ 0 &{} \text{ otherwise } \\ \end{array}\right. \end{aligned}$$

(2)

The adjacency matrix contains the whole information about the network.

In our case, the nodes are identical with the spherical droplets. An edge exists if the distance between the midpoints of two droplets is smaller than the sum of their radii, i.e.,

$$\begin{aligned} \sqrt{(x_i-x_j)^2 + (y_i-y_j)^2 + (z_i-z_j)^2} \le r_i+r_j+\theta \end{aligned}$$

(3)

with some threshold value $\theta$, which needs not only to be introduced because of numerical inaccuracy but also in order to consider the short DNA strands connecting pairs of droplets, and if some further constraints are met, e.g., that only connections between red and green droplets can be formed [20]. Please note that $\theta$ can be negative and depend on $r_i$ and $r_j$ if the droplets lose their spherical shapes in the case of extended bilayer formation.

4.1 Analyzing one Network

One can take different viewpoints when analyzing such a network: On the local or elementary level, one considers the properties of the nodes, e.g., the degree D(i) of a node i, which is the number of connections node i has to other nodes and which can be easily derived from the adjacency matrix by $D(i)=\sum _j \eta (i,j)$. On an intermediate level, groups of nodes are considered like the question what the maximum clique size is, i.e., the maximum number of nodes in a subset of the graph which are pairwise connected with each other. From a global viewpoint, the properties of the overall network are studied. One such property is the maximum of the geodesic distances between pairs of nodes. The geodesic distance d(i, j) between two specific nodes i and j is the minimum number of edges which have to be trespassed to get from i to j. Another widely studied question is whether the network is contiguous or whether it is split in a number of clusters, how large the number of these clusters is, and how large the size of the largest cluster is [24]. Please note that we refer to a cluster as a subset of nodes in which each node can be reached from any other node in the same cluster by using only edges connecting the nodes of this cluster. In contrast, a clique is defined as a subset of nodes in which all of these nodes are directly connected with each other by an edge. Finally, one can also take a local-global viewpoint and e.g. study the importance of specific nodes for the overall network [16]. Figure 6 shows exemplary results for the time evolution of some of these observables during a simulation.

4.2 Comparing Networks

So far, we have only analyzed networks separately. Of course, we can then perform statistics of the properties of these networks and can have a look at how these statistics change if experimental parameters are altered. However, for our purposes, we want to generate exactly the same networks or at least networks with equal parts again and again. Thus, we have also to compare networks. But already finding out whether two networks are identical is far from being a trivial task as shown in Fig. 5.

Fig. 5.

Toy example for the graph isomorphism problem: The two networks shown above are comprised of 5 nodes and 7 edges each and are seemingly different. But one can map them onto each other by the isomorphism $E=3, A=5, B=4, D=1,$ and $C=2$.

Usually, no isomorphisms between entire networks can be found, such that one has to restrict oneself to the detection of common structures like a common subnetwork. Then one can group the various networks according to the commonly detected subnetworks. For this purpose, we intend to e.g. extend the k-shell decomposition algorithm [2] for determining whether a common network nucleus exists and which fractal subcomponents exist in various configurations.

5 How to Understand, Simulate, and Plan the Agglomeration Process

5.1 Simulating the Agglomeration

So far, we have only spoken about the experiments performed and the analysis of the experimental outcomes. But in order to truly understand the agglomeration of droplets, we have to develop a simplified model, simulate this model on a computer, thus mimicking the experiment, and compare the results of the simulations with the experimental findings. If they deviate, then the model has to be adjusted or perhaps even another model has to be developed. However, each model has to be built on physical laws. So, each droplet sinks in water due to gravity reduced by the buoyant force. Due to its spherical shape, we also apply the Stokes friction force $\boldsymbol{F}_{i,\textrm{S}}=-6\pi \eta r_i \boldsymbol{v}_i$ to it as well as the added mass concept [25]. However, these last laws do not consider the hydrophilic nature of the surface of the droplet, which might slightly alter these laws. Furthermore, we add some small random velocity changes to simulate the motion induced in the experimental setup, which cannot be modeled exactly, and almost-elastic collision laws if droplets touch each other or the surface.

Figure 6 presents the time evolution of some observables in network analysis. For the simulations, the same parameters were used as in [20] with 2,000 droplets initialized in an inner part of a cylinder only (“narrow initialization”). This leads to significant qualitative and quantitative differences to results presented in [19], in which a “wide initialization” routine was implemented, for which the whole cylinder volume was used.

Of course, these simulation results will not coincide exactly with experimental findings. However, in an iterative process with analyzing pictures and movies from experiments, the model parameters have to be gradually changed. Then a simulation finally mimicks an experiment much better than in our current results shown in Fig. 7, perhaps not in the exact trajectories of the various particles, but in the statistics created of all particles.

5.2 Planning the Gradual Reaction Scheme

The theoretical and analytical work so far followed a bottom-up approach by starting either from physical laws for modelling and simulating the experimental setup or starting from pictures taken from experimental outcomes which are then analyzed. On the other hand, we would also like to follow a top-down approach by starting at the desired results and then gradually taking steps down in order to better plan these last steps towards this goal, which later on shall become the first steps.

Fig. 6.

Time evolution of network observables during a simulation (see Sect. 5) of a polydisperse system of droplets with two types of particles (curves marked as “2 colors”: “red” R and “green” G): only $R-G$ connections can be formed but not $R-R$ and not $G-G$. For comparison, also the results for the scenario that only one type of particles exists are shown (curves marked as “1 color”). Top: mean value (left) and maximum (right) of degrees of the droplets. Middle: mean value (left) and maximum (right) of geodesic distances between pairs of droplets. Bottom: number of clusters (left) and maximum cluster size (right).

As already mentioned, among other aims, we intend to produce macromolecules using the technology of a chemical compiler we intend to develop. For this purpose, we first need to know how to produce these macromolecules in order to plan the gradual reaction scheme. For many pharmaceutical macromolecules, various ways are known how to synthesize them [9]. Using small droplets, we think that further methods to produce these macromolecules could be developed as the compartimentalization of usually semi-stable molecules might stabilize them, thus offering new possibilities for synthesis methods.

5.3 Designing the Arrangement of Droplets with Geometric and Physical Restrictions

The plan of the gradual reaction scheme has to be translated into a network of droplets. Trivially, the nodes represent the droplets being filled with the educts. But already at this point, one has to consider which relative quantities of educts and thus which relative radii of droplets are needed. Then there are edges between those nodes between which there are chemical reactions during the first step of the gradual reaction scheme. But then the question arises how to move on. There are various ways conceivable of how to implement the second step of the gradual reaction scheme. For example, those groups of droplets which together produced some intermediary product in the first step could be enclosed in a further hull into which they emit the resulting molecules of this first reaction step. Another possibility would be that these groups of droplets unite to one larger droplet. In these two cases, these groups of droplets are then represented by a super-node, and the super-nodes are then connected with edges representing chemical reactions between them in the second step of the gradual reaction scheme. This approach could then be iterated for the remaining steps. But a third possibility could be that the intermediary product of a chemical reaction could be found preferrably in one of the droplets only. Then its representing node has to be connected by edges with reaction partners in the next reaction step. Thus, in this approach, we will have edges which are typically only active for one reaction step, resulting in an adjacency matrix $\eta (i,j,t)$ with (i, j) denoting the pair of droplets between which a chemical reaction shall take place and t denoting the time step at which this chemical reaction shall be performed in the gradual reaction scheme. In the experiment, additional difficulties arise to activate or deactivate specific connections for specific reaction steps.

Fig. 7.

Time evolution of an experimental agglomeration process (top row) and of a computer simulation trying to mimick the experiment (bottom row)

In order to translate the network of droplets into a real agglomeration, it might not only be necessary

• to work with droplets of different sizes, referring to the relative amount of chemicals needed for the reaction process, but also of different weights, i.e., to work with droplets filled with oils of differing densities, in which the chemicals are hosted,

• to work with various types of sticks on droplet surfaces, such that e.g. not only “$A-B$” connections but also “$A-C$” connections can be formed,

• to develop sticks beyond the concept of complementary ssDNA strands, so that connections for successive steps in the gradual reaction scheme can be formed.

Fig. 8.

While up to 12 spheres of equal radius can touch a sphere of the same radius in their midst without overlaps, already 28 spheres of equal radius can touch the sphere in their midst if its radius is twice as large [18].

However, for such a reaction network and a corresponding agglomeration of droplets, physical and geometric restrictions have to be taken into account. For some of these restrictions, one can exploit findings from related areas of research. For example, some decades ago Newton’s solution to the so-called kissing number problem was proved to be correct, according to which only up to 12 spheres of equal radius can touch a further sphere of the same radius in their midst without overlaps [26]. Another related problem, the question what the maximum number of connections in a set of N sticky spheres of equal radius can be has been solved for small values of N [7]. However, we have to take into account that our droplets differ in size, such that we do not deal with a monodisperse but a polydisperse system. Already for other problems like the “circles in a circle” problem [14], it has been shown that the polydispersity significantly changes the results [12] and the nature [17] of this problem. In order to get better estimates for extreme values of a polydisperse system of touching spheres, we developed a heuristic for a bidisperse kissing number problem [18], which e.g. led to the conclusion that up to 28 spheres of radius 1 can touch a sphere of radius 2 in their midst, as shown in Fig. 8, thus providing a maximum number of kissing spheres in a polydisperse system in which the maximum radius is only twice as large as the smallest one.

And, finally, we have to find out how to design the experiment in a way that it indeed produces the desired agglomeration of droplets with the reaction network within, which in turn runs the gradual reaction scheme leading to the desired molecules. For this final step, we have to combine all findings from all the steps described above.

6 Conclusion and Outlook

In this paper, we have described several obstacles we have met on our pathway to build a chemical compiler. It shall be able to foretell how an experiment has to be designed in order to generate an agglomeration of droplets with which a gradual chemical reaction scheme can be enabled for the purpose of producing some specific macromolecule. But it can also be helpful to answer basic questions for the origin of life [13], e.g., which molecules could be produced with which probability if their educts were not simply mixed in a primordial soup but compartementalized in droplets which are then brought in contact with each other. This technology could also find an application as environment or medical biosensor. A further application might be the investigation and reproduction of metabolic catalysis in living beings as well as the creation of their counterparts for artificial lifeforms.

But before thinking of possible applications of such a device, we first have to find solutions for various problems. We have to find a reliable and reproducable way of generating droplets of various specific sizes, have to develop a method to automatically analyze pictures taken from their agglomeration, have to change our models for this agglomeration process, such that they mimick the experiments, and have to check with tools from network analysis whether we indeed generate the desired gradual reaction network as intended.