Skip to main content
Springer Nature Link
Log in

On Three Domination-Based Identification Problems in Block Graphs

  • Conference paper
  • First Online:
Algorithms and Discrete Applied Mathematics (CALDAM 2023)

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 13947))

Included in the following conference series:

  • 519 Accesses

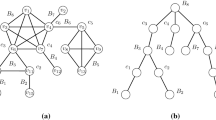
Abstract

The problems of determining the minimum-sized identifying, locating-dominating and open locating-dominating codes of an input graph are special search problems that are challenging from both theoretical and computational viewpoints. In these problems, one selects a dominating set C of a graph G such that the vertices of a chosen subset of V(G) (i.e. either \(V(G)\setminus C\) or V(G) itself) are uniquely determined by their neighborhoods in C. A typical line of attack for these problems is to determine tight bounds for the minimum codes in various graph classes. In this work, we present tight lower and upper bounds for all three types of codes for block graphs (i.e. diamond-free chordal graphs). Our bounds are in terms of the number of maximal cliques (or blocks) of a block graph and the order of the graph. Two of our upper bounds verify conjectures from the literature - with one of them being now proven for block graphs in this article. As for the lower bounds, we prove them to be linear in terms of both the number of blocks and the order of the block graph. We provide examples of families of block graphs whose minimum codes attain these bounds, thus showing each bound to be tight.

This work was sponsored by a public grant overseen by the French National Research Agency as part of the “Investissements d’Avenir” through the IMobS3 Laboratory of Excellence (ANR-10-LABX-0016) and the IDEX-ISITE initiative CAP 20-25 (ANR-16-IDEX-0001). We also acknowledge support of the ANR project GRALMECO (ANR-21-CE48-0004).

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Argiroffo, G.R., Bianchi, S.M., Lucarini, Y., Wagler, A.K.: On the identifying code number of block graphs. In: Proceedings of ICGT 2018, Lyon, France (2018)

    Google Scholar 

  2. Argiroffo, G.R., Bianchi, S.M., Lucarini, Y., Wagler, A.K.: Linear-time algorithms for three domination-based separation problems in block graphs. Discret. Appl. Math. 281, 6–41 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  3. Argiroffo, G., Bianchi, S., Wagler, A.: Study of identifying code polyhedra for some families of split graphs. In: Fouilhoux, P., Gouveia, L.E.N., Mahjoub, A.R., Paschos, V.T. (eds.) ISCO 2014. LNCS, vol. 8596, pp. 13–25. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-09174-7_2

    Chapter  Google Scholar 

  4. Balbuena, C., Foucaud, F., Hansberg, A.: Locating-dominating sets and identifying codes in graphs of girth at least 5. Electron. J. Comb. 22, P2.15 (2015)

    Google Scholar 

  5. Bertrand, N., Charon, I., Hudry, O., Lobstein, A.: 1-identifying codes on trees. Australas. J Comb. 31, 21–36 (2005)

    MathSciNet  MATH  Google Scholar 

  6. Bousquet, N., Lagoutte, A., Li, Z., Parreau, A., Thomassé, S.: Identifying codes in hereditary classes of graphs and VC-dimension. SIAM J. Discret. Math. 29(4), 2047–2064 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  7. Charon, I., Hudry, O., Lobstein, A.: Minimizing the size of an identifying or locating-dominating code in a graph is NP-hard. Theoret. Comput. Sci. 290(3), 2109–2120 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  8. Chlebus, B.S., Nguyen, S.H.: On finding optimal discretizations for two attributes. In: Polkowski, L., Skowron, A. (eds.) RSCTC 1998. LNCS (LNAI), vol. 1424, pp. 537–544. Springer, Heidelberg (1998). https://doi.org/10.1007/3-540-69115-4_74

    Chapter  Google Scholar 

  9. Foucaud, F., Lehtilä, T.: Revisiting and improving upper bounds for identifying codes. SIAM J. Discret. Math. 36(4), 2619–2634 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  10. Foucaud, F.: Decision and approximation complexity for identifying codes and locating-dominating sets in restricted graph classes. J. Discret. Algorithms 31, 48–68 (2015). https://doi.org/10.1016/j.jda.2014.08.004

    Article  MathSciNet  MATH  Google Scholar 

  11. Foucaud, F., Ghareghani, N., Roshany-Tabrizi, A., Sharifani, P.: Characterizing extremal graphs for open neighbourhood location-domination. Discret. Appl. Math. 302, 76–79 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  12. Foucaud, F., Gravier, S., Naserasr, R., Parreau, A., Valicov, P.: Identifying codes in line graphs. J. Graph Theory 73(4), 425–448 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  13. Foucaud, F., Henning, M.A.: Location-domination and matching in cubic graphs. Discret. Math. 339(4), 1221–1231 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  14. Foucaud, F., Mertzios, G.B., Naserasr, R., Parreau, A., Valicov, P.: Identification, location-domination and metric dimension on interval and permutation graphs. I. bounds. Theor. Comput. Sci. 668, 43–58 (2017). https://doi.org/10.1016/j.tcs.2017.01.006

  15. Foucaud, F., Mertzios, G.B., Naserasr, R., Parreau, A., Valicov, P.: Identification, location-domination and metric dimension on interval and permutation graphs. II. Algorithms and complexity. Algorithmica 78(3), 914–944 (2017)

    Google Scholar 

  16. Garijo, D., González, A., Márquez, A.: The difference between the metric dimension and the determining number of a graph. Appl. Math. Comput. 249, 487–501 (2014)

    MathSciNet  MATH  Google Scholar 

  17. Harary, F.: A characterization of block-graphs. Can. Math. Bull. 6(1), 1–6 (1963)

    Article  MathSciNet  MATH  Google Scholar 

  18. Henning, M.A., Yeo, A.: Distinguishing-transversal in hypergraphs and identifying open codes in cubic graphs. Graphs Comb. 30, 909–932 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  19. Howorka, E.: On metric properties of certain clique graphs. J. Comb. Theory Ser. B 27(1), 67–74 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  20. Karpovsky, M.G., Chakrabarty, K., Levitin, L.B.: On a new class of codes for identifying vertices in graphs. IEEE Trans. Inf. Theory 44(2), 599–611 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  21. Moret, B.M.E., Shapiro, H.D.: On minimizing a set of tests. SIAM J. Sci. Stat. Comput. 6(4), 983–1003 (1985)

    Article  Google Scholar 

  22. Rall, D.F., Slater, P.J.: On location-domination numbers for certain classes of graphs. Congr. Numer. 45, 97–106 (1984)

    MathSciNet  MATH  Google Scholar 

  23. Rao, N.: Computational complexity issues in operative diagnosis of graph-based systems. IEEE Trans. Comput. 42(4), 447–457 (1993)

    Article  Google Scholar 

  24. Rényi, A.: On random generating elements of a finite boolean algebra. Acta Scientiarum Mathematicarum Szeged 22, 75–81 (1961)

    MathSciNet  MATH  Google Scholar 

  25. Seo, S.J., Slater, P.J.: Open neighborhood locating dominating sets. Australas. J. Comb. 46, 109–120 (2010)

    MathSciNet  MATH  Google Scholar 

  26. Slater, P.J.: Domination and location in acyclic graphs. Networks 17(1), 55–64 (1987)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Université Clermont-Auvergne, CNRS, Mines de Saint-Étienne, Clermont-Auvergne-INP, LIMOS, 63000, Clermont-Ferrand, France

    Dipayan Chakraborty, Florent Foucaud & Annegret K. Wagler

  2. Univ Lyon, CNRS, INSA Lyon, UCBL, Centrale Lyon, Univ Lyon 2, LIRIS, UMR5205, F-69622, Villeurbanne, France

    Aline Parreau

Authors
  1. Dipayan Chakraborty
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Florent Foucaud
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Aline Parreau
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Annegret K. Wagler
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Florent Foucaud .

Editor information

Editors and Affiliations

  1. Department of Computer Science and Engineering, Indian Institute of Technology Delhi, New Delhi, India

    Amitabha Bagchi

  2. Dhirubhai Ambani Institute of Information and Communication Technology, Gandhinagar, India

    Rahul Muthu

Rights and permissions

Reprints and permissions

Copyright information

© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Chakraborty, D., Foucaud, F., Parreau, A., Wagler, A.K. (2023). On Three Domination-Based Identification Problems in Block Graphs. In: Bagchi, A., Muthu, R. (eds) Algorithms and Discrete Applied Mathematics. CALDAM 2023. Lecture Notes in Computer Science, vol 13947. Springer, Cham. https://doi.org/10.1007/978-3-031-25211-2_21

Download citation

  • DOI: https://doi.org/10.1007/978-3-031-25211-2_21

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-031-25210-5

  • Online ISBN: 978-3-031-25211-2

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics