Abstract
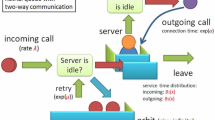
This paper considers a mathematical model of a cyclic multiple access communication network. The model can be used to build specialized “flying” FANET data transmission networks. We consider a single server retrial queue for modeling one node in such network. The input consists of multiple Poisson processes with different arrival rates. Service and retrial rates depend on the origin flow. Thus, each flow has its own orbit for redial. Under the condition when the retrial rate is low, we obtain an asymptotic probability distribution of the number of customers in the orbits.
This study was supported by the Tomsk State University Development Programme (Priority-2030).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Khan, M.F., Yau, K.-L.A., Noor, R.M., Imran, M.A.: Routing schemes in FANETs: a survey. Sensors 20, 38 (2020)
Artalejo, J.R.: Accessible bibliography on retrial queues: progress in 2000–2009. Math. Comput. Model. 51(9–10), 1071–1081 (2010)
Artalejo, J.R.: A classified bibliography of research on retrial queues: progress in 1990–1999. TOP 7(2), 187–211 (1999)
Artalejo, J.R., Gómez-Corral, A.: Retrial queueing systems: a computational approach. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78725-9
Artalejo, J.R., Falin, G.I.: Standard and retrial queueing systems: a comparative analysis. Revista Matematica Complutense 15, 101–129 (2002)
Vishnevskii, V., Semenova, O.: Sistemy pollinga: teoriya i primenenie v shirokopolosnykh besprovodnykh setyakh [Polling systems: theory and applications in broadband wireless networks], 312 p. Tekhnosfera Publ., Moscow (2007)
Vishnevskii, V., Semenova, O.: Mathematical research methods polling systems. Autom. Telemechanics 2, 3–56 (2006)
Nazarov, A., Paul, S.: A cyclic queueing system with priority customers and T-strategy of service. Commun. Comput. Inf. Sci. 678, 182–193 (2016)
Nazarov, A., Paul, S.: A number of customers in the system with server vacations. Commun. Comput. Inf. Sci. 601, 334–343 (2015)
Nazarov, A.A., Paul, S.V., Klyuchnikova, P.N.: Research of a cyclic system with repeated calls. In: Distributed Computer and Telecommunication Networks: Control, Calculation, Communication (DCCN-2020), 14–18 September 2020, Moscow, Russia (2020)
Langaris, C.: A polling model with retrial customers. J. Oper. Res. Soc. Japan 40(4), 489–508 (1997)
Langaris, C.: Gated polling models with customers in orbit. Math. Comput. Model. 30(3–4), 171–187 (1999)
Langaris, C.: Markovian polling system with mixed service disciplines and retrial customers. TOP 7, 305–322 (1999)
Boxma, O., Resing, J.: Vacation and polling models with retrials. In: Horváth, A., Wolter, K. (eds.) EPEW 2014. LNCS, vol. 8721, pp. 45–58. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10885-8_4
Abidini, M.A., Boxma, O., Resing, J.: Analysis and optimization of vacation and polling models with retrials. Perform. Eval. 98, 52–69 (2016)
Moiseev, A., Nazarov, A., Paul, S.: Asymptotic diffusion analysis of multi-server retrial queue with hyper-exponential service. Mathematics 8(4), 531 (2020)
Nazarov, A., Phung-Duc, T., Paul, S., Lizyura, O.: Diffusion limit for single-server retrial queues with renewal input and outgoing calls. Mathematics 10(6), 948 (2022)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 ICST Institute for Computer Sciences, Social Informatics and Telecommunications Engineering
About this paper
Cite this paper
Nazarov, A., Phung-Duc, T., Shulgina, K., Lizyura, O., Paul, S., Shashev, D. (2023). Cyclic Retrial Queue for Building Data Transmission Networks. In: Hyytiä, E., Kavitha, V. (eds) Performance Evaluation Methodologies and Tools. VALUETOOLS 2022. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, vol 482. Springer, Cham. https://doi.org/10.1007/978-3-031-31234-2_10
Download citation
DOI: https://doi.org/10.1007/978-3-031-31234-2_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-31233-5
Online ISBN: 978-3-031-31234-2
eBook Packages: Computer ScienceComputer Science (R0)