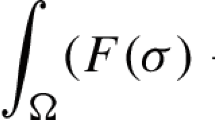Abstract
We state the Limited Electrode problem in Electrical Impedance Tomography, and propose solutions inspired by the application of compressed sensing techniques and deep learning strategies on the raw boundary impedance data. These strategies allow to recover the target reconstruction quality while using a relatively low number of nonlinear measurements, assuming sparsity-gradient conductivity. This would help reducing modelling costs and computational power, thus enhancing applicability of EIT.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Alberti, G.S., Santacesaria, M.: Calderón’s inverse problem with a finite number of measurements. Forum Math. Sigma. 7, e35 (2019). https://doi.org/10.1017/fms.2019.31
Alberti, G.S., Santacesaria, M.: Infinite dimensional compressed sensing from anisotropic measurements and applications to inverse problems in PDE. Appl. Comput. Harmon. Anal. 50, 105–146 (2021). https://doi.org/10.1016/j.acha.2019.08.002
Blumensath, T.: Compressed sensing with nonlinear observations and related nonlinear optimization problems. IEEE Trans. Inf. Theory. 59(6), 3466–3474, 2245716 (2013). https://doi.org/10.1109/TIT.2013
Borsic, A., et al.: In Vivo impedance imaging with total variation regularization. IEEE Trans. Med. Imaging. 29(1), 44–54 (2010). https://doi.org/10.1109/TMI.2009.2022540
Candès, E.J., Romberg, J.K., Tao, T.: Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 59(8), 1207–1223 (2006). https://doi.org/10.1002/cpa.20124
Colibazzi, F., Lazzaro, D., Morigi, S., Samoré, A.: Learning nonlinear electrical impedance tomography. J. Sci. Comput. 90(1), 1–23 (2021). https://doi.org/10.1007/s10915-021-01716-4
Cortesi, M., et al.: Development of an electrical impedance tomography set-up for the quantification of mineralization in biopolymer scaffolds. Physiol. Measur. 42(6), 064001 (2021). https://doi.org/10.1088/1361-6579/ac023b
Harrach, B.: Uniqueness and Lipschitz stability in electrical impedance tomography with finitely many electrodes. Inverse Prob. 35(2), 024005 (2019). https://doi.org/10.1088/1361-6420/aaf6fc
Jauhiainen, J., et al.: Relaxed Gauss-Newton methods with applications to electrical impedance tomography. SIAM J. Imaging Sci. 13(3), 1415–1445 (2020). https://doi.org/10.1137/20M1321711
Somersalo, E., Cheney, M., Isaacson, D.: Existence and uniqueness for electrode models for electric current computed tomography. SIAM J. Appl. Math. 52(4), 1023–1040 (1992). https://doi.org/10.1137/0152060
Tallman, T.N., Smyl, D.J.: Structural health and condition monitoring via electrical impedance tomography in self-sensing materials: a review. Smart Mater. Struct. 29(12), 123001 (2020). https://doi.org/10.1088/1361-665X/abb352
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
7.1 Appendix: regularized Gauss-Newton method for the inverse EIT problem
7.1 Appendix: regularized Gauss-Newton method for the inverse EIT problem
Given a nonlinear residual \(r(\sigma )\), the ill-posedness of problem (1) can be alleviated by adding to the cost function a regularization term \(R(\sigma )\), which stabilizes the solution
with \(\alpha >0\) the regularization parameter. An approximated solution of the unconstrained regularized nonlinear minimization problem (7) can be obtained by applying the iterative Regularized Gauss-Newton (RGN) method, which, starting from an initial guess \(\sigma ^{(0)}\), performs a line search along the direction \(p^{(k)}\) to obtain the new conductivity iterate \(\sigma ^{(k+1)}= \sigma ^{(k)} + p^{(k)}\), following the search direction \(p^{(k)}\) from the current iterate.
For the choice \(R(\sigma ):= \Vert \nabla \sigma \Vert _2^2\), the functional in (7) is the classical generalized nonlinear Tikhonov model, a standard choice in EIT [4], and the (RGN) method can be applied with \(p^{(k)}\) determined by solving the linear normal equations
where \(L^TL \in {\mathbb R}^{n_T \times n_T}\) denotes the Laplacian. In case the total variation regularizer \(R(\sigma )=\Vert \nabla \sigma \Vert _1 \) is considered, we can resort to the discretization presented in [4], with \(R(\sigma ) \approx D^TE^{-1}D\), with D denoting the discrete gradient, and \(E=1/diag(\sqrt{(D\sigma )^2+\epsilon ^2})\), \(\bar{D}=\sqrt{E} D\). The direction \(p^{(k)}\) is then obtained by solving the linear normal equations
The linear systems in RGN-Tik and RGN-TV are solved by a few iterations of the conjugate gradient method.
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Colibazzi, F., Lazzaro, D., Morigi, S., Samorè, A. (2023). Limited Electrodes Models in Electrical Impedance Tomography Reconstruction. In: Calatroni, L., Donatelli, M., Morigi, S., Prato, M., Santacesaria, M. (eds) Scale Space and Variational Methods in Computer Vision. SSVM 2023. Lecture Notes in Computer Science, vol 14009. Springer, Cham. https://doi.org/10.1007/978-3-031-31975-4_6
Download citation
DOI: https://doi.org/10.1007/978-3-031-31975-4_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-31974-7
Online ISBN: 978-3-031-31975-4
eBook Packages: Computer ScienceComputer Science (R0)