Abstract
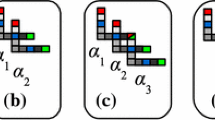
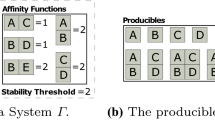
Two significant and often competing goals within the field of self-assembly are minimizing tile types and minimizing human-mediated experimental operations. The introduction of the Staged Assembly and Single Staged Assembly models, while successful in the former aim, necessitate an increase in mixing operations later. In this paper, we investigate building optimal lines as a standard benchmark shape and building primitive. We show that a restricted version of the 1D Staged Assembly Model can be simulated by the 1D Freezing Tile Automata model with the added benefits of the complete automation of stages and completion in a single bin while maintaining bin parallelism and a competitive number of states for lines, patterned lines, and context-free grammars.
This research was supported in part by National Science Foundation Grant CCF-1817602.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Typical TA models are defined with a temperature parameter \(\tau \) however, with consideration of solely 1D, eliminating the possibility of cooperative binding, we assume \(\tau = 1\).
- 2.
Each bin may be seen as an instance of the 2-Handed Assembly Model.
References
Alaniz, R.M., et al.: Building squares with optimal state complexity in restricted active self-assembly. In: Proceedings of the Symposium on Algorithmic Foundations of Dynamic Networks, SAND 2022, vol. 221, pp. 6:1–6:18 (2022)
Alumbaugh, J.C., Daymude, J.J., Demaine, E.D., Patitz, M.J., Richa, A.W.: Simulation of programmable matter systems using active tile-based self-assembly. In: Thachuk, C., Liu, Y. (eds.) DNA 2019. LNCS, vol. 11648, pp. 140–158. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26807-7_8
Barad, G., et al.: Simulation of one dimensional staged dna tile assembly by the signal-passing hierarchical tam. Procedia Comput. Sci. 159, 1918–1927 (2019)
Benz, F., Kötzing, T.: An effective heuristic for the smallest grammar problem. In: Proceedings of the 15th Annual Conference on Genetic and Evolutionary Computation, pp. 487–494 (2013)
Caballero, D., Gomez, T., Schweller, R., Wylie, T.: Verification and computation in restricted tile automata. In: 26th International Conference on DNA Computing and Molecular Programming, DNA 2020, vol. 174, pp. 10:1–10:18 (2020)
Caballero, D., Gomez, T., Schweller, R., Wylie, T.: Covert computation in staged self-assembly: verification is pspace-complete. In: 29th Annual European Symposium on Algorithms, ESA 2021, pp. 23:1–23:18 (2021)
Cannon, S., et al.: Two hands are better than one (up to constant factors): self-assembly in the 2HAM vs. aTAM. In: 30th Inter. Sym. on Theoretical Aspects of Computer Science, STACS 2013, vol. 20, pp. 172–184 (2013)
Cantu, A.A., Luchsinger, A., Schweller, R., Wylie, T.: Signal passing self-assembly simulates tile automata. In: 31st International Symposium on Algorithms and Computation, ISAAC 2020, pp. 53:1–53:17 (2020)
Chalk, C., Luchsinger, A., Martinez, E., Schweller, R., Winslow, A., Wylie, T.: Freezing simulates non-freezing tile automata. In: Doty, D., Dietz, H. (eds.) DNA 2018. LNCS, vol. 11145, pp. 155–172. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-00030-1_10
Chalk, C., Martinez, E., Schweller, R., Vega, L., Winslow, A., Wylie, T.: Optimal staged self-assembly of general shapes. Algorithmica 80(4), 1383–1409 (2018)
Chalk, C., Martinez, E., Schweller, R., Vega, L., Winslow, A., Wylie, T.: Optimal staged self-assembly of linear assemblies. Nat. Comput. 18(3), 527–548 (2019). https://doi.org/10.1007/s11047-019-09740-y
Demaine, E.D., et al.: Staged self-assembly: nanomanufacture of arbitrary shapes with o (1) glues. Nat. Comput. 7(3), 347–370 (2008)
Demaine, E.D., Eisenstat, S., Ishaque, M., Winslow, A.: One-dimensional staged self-assembly. In: Proceedings of the 17th International Conference on DNA Computing and Molecular Programming, DNA 2011, pp. 100–114 (2011)
Schweller, R., Winslow, A., Wylie, T.: Verification in staged tile self-assembly. Nat. Comput. 18(1), 107–117 (2019)
Thubagere, A.J., et al.: A cargo-sorting DNA robot. Science 357(6356), eaan6558 (2017)
Tikhomirov, G., Petersen, P., Qian, L.: Fractal assembly of micrometre-scale dna origami arrays with arbitrary patterns. Nature 552(7683), 67–71 (2017)
Winfree, E.: Algorithmic Self-Assembly of DNA. Ph.D. thesis, California Institute of Technology (June 1998)
Winslow, A.: Staged self-assembly and polyomino context-free grammars. Nat. Comput. 14(2), 293–302 (2015)
Woods, D., Doty, D., Myhrvold, C., Hui, J., Zhou, F., Yin, P., Winfree, E.: Diverse and robust molecular algorithms using reprogrammable dna self-assembly. Nature 567(7748), 366–372 (2019)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Cirlos, S.C., Gomez, T., Grizzell, E., Rodriguez, A., Schweller, R., Wylie, T. (2023). Simulation of Multiple Stages in Single Bin Active Tile Self-assembly. In: Genova, D., Kari, J. (eds) Unconventional Computation and Natural Computation. UCNC 2023. Lecture Notes in Computer Science, vol 14003. Springer, Cham. https://doi.org/10.1007/978-3-031-34034-5_11
Download citation
DOI: https://doi.org/10.1007/978-3-031-34034-5_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-34033-8
Online ISBN: 978-3-031-34034-5
eBook Packages: Computer ScienceComputer Science (R0)