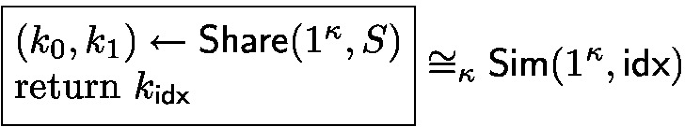Abstract
Structure-Aware private set intersection (sa-PSI) is a variant of PSI where Alice’s input set A has some publicly known structure, Bob’s input B is an unstructured set of points, and Alice learns the intersection \(A \cap B\). sa-PSI was recently introduced by Garimella et al. (Crypto 2022), who described a semi-honest protocol with communication that scales with the description size of Alice’s set, instead of its cardinality. In this paper, we present the first sa-PSI protocol secure against malicious adversaries.
sa-PSI protocols are built from function secret sharing (FSS) schemes, and the main challenge in our work is ensuring that multiple FSS sharings encode the same structured set. We do so using a cut-and-choose approach. In order to make FSS compatible with cut-and-choose, we introduce a new variant of function secret sharing, called derandomizable FSS (dFSS).
We show how to construct dFSS for union of geometric balls, leading to a malicious-secure sa-PSI protocol where Alice’s input is a union of balls. We also improve prior FSS constructions, giving asymptotic improvements to semi-honest sa-PSI.
G. Garimella, M. Rosulek and J. Singh—Authors partially supported by NSF award S2356A.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
Beaver, D.: Precomputing oblivious transfer. In: Coppersmith, D. (ed.) CRYPTO 1995. LNCS, vol. 963, pp. 97–109. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-44750-4_8
Boneh, D., Boyle, E., Corrigan-Gibbs, H., Gilboa, N., Ishai, Y.: Lightweight techniques for private heavy hitters. In: 2021 IEEE Symposium on Security and Privacy (SP), pp. 762–776. IEEE (2021)
Boyle, E., et al.: Function secret sharing for mixed-mode and fixed-point secure computation. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12697, pp. 871–900. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77886-6_30
Boyle, E., Couteau, G., Gilboa, N., Ishai, Y.: Compressing vector OLE. In: Lie, D., Mannan, M., Backes, M., Wang, X. (eds.) ACM CCS 2018, pp. 896–912. ACM Press, October 2018
Boyle, E., et al.: Efficient two-round OT extension and silent non-interactive secure computation. In: Cavallaro, L., Kinder, J., Wang, X., Katz, J. (eds.) ACM CCS 2019, pp. 291–308. ACM Press, November 2019
Boyle, E., Couteau, G., Gilboa, N., Ishai, Y., Kohl, L., Scholl, P.: Efficient pseudorandom correlation generators: silent OT extension and more. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part III. LNCS, vol. 11694, pp. 489–518. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_16
Boyle, E., Gilboa, N., Ishai, Y.: Function secret sharing. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 337–367. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_12
Boyle, E., Gilboa, N., Ishai, Y.: Function secret sharing: improvements and extensions. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, pp. 1292–1303 (2016)
Boyle, E., Gilboa, N., Ishai, Y.: Secure computation with preprocessing via function secret sharing. In: Hofheinz, D., Rosen, A. (eds.) TCC 2019. LNCS, vol. 11891, pp. 341–371. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-36030-6_14
Boyle, E., Gilboa, N., Ishai, Y., Kolobov, V.I.: Programmable distributed point functions. Cryptology ePrint Archive (2022)
Chase, M., Miao, P.: Private set intersection in the internet setting from lightweight oblivious PRF. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020, Part III. LNCS, vol. 12172, pp. 34–63. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56877-1_2
Couteau, G., Rindal, P., Raghuraman, S.: Silver: silent VOLE and oblivious transfer from hardness of decoding structured LDPC codes. In: Malkin, T., Peikert, C. (eds.) CRYPTO 2021, Part III. LNCS, vol. 12827, pp. 502–534. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84252-9_17
Dachman-Soled, D., Malkin, T., Raykova, M., Yung, M.: Efficient robust private set intersection. In: Abdalla, M., Pointcheval, D., Fouque, P.-A., Vergnaud, D. (eds.) ACNS 2009. LNCS, vol. 5536, pp. 125–142. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01957-9_8
Dachman-Soled, D., Malkin, T., Raykova, M., Yung, M.: Secure efficient multiparty computing of multivariate polynomials and applications. In: Lopez, J., Tsudik, G. (eds.) ACNS 2011. LNCS, vol. 6715, pp. 130–146. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21554-4_8
de Castro, L., Polychroniadou, A.: Lightweight, maliciously secure verifiable function secret sharing. In: Dunkelman, O., Dziembowski, S. (eds.) EUROCRYPT 2022. LNCS, vol. 13275, pp. 150–179. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-06944-4_6
De Cristofaro, E., Kim, J., Tsudik, G.: Linear-complexity private set intersection protocols secure in malicious model. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 213–231. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_13
De Cristofaro, E., Tsudik, G.: Practical private set intersection protocols with linear complexity. In: Sion, R. (ed.) FC 2010. LNCS, vol. 6052, pp. 143–159. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14577-3_13
Dong, C., Chen, L., Wen, Z.: When private set intersection meets big data: an efficient and scalable protocol. In: Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) ACM CCS 2013, pp. 789–800. ACM Press, November 2013
Frederiksen, T.K., Jakobsen, T.P., Nielsen, J.B., Trifiletti, R.: On the complexity of additively homomorphic UC commitments. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 542–565. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_23
Freedman, M.J., Ishai, Y., Pinkas, B., Reingold, O.: Keyword search and oblivious pseudorandom functions. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 303–324. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_17
Freedman, M.J., Nissim, K., Pinkas, B.: Efficient private matching and set intersection. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 1–19. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_1
Garimella, G., Mohassel, P., Rosulek, M., Sadeghian, S., Singh, J.: Private set operations from oblivious switching. In: Garay, J.A. (ed.) PKC 2021, Part II. LNCS, vol. 12711, pp. 591–617. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-75248-4_21
Garimella, G., Pinkas, B., Rosulek, M., Trieu, N., Yanai, A.: Oblivious key-value stores and amplification for private set intersection. In: Malkin, T., Peikert, C. (eds.) CRYPTO 2021, Part II. LNCS, vol. 12826, pp. 395–425. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84245-1_14
Garimella, G., Rosulek, M., Singh, J.: Structure-aware private set intersection, with applications to fuzzy matching. In: Dodis, Y., Shrimpton, T. (eds.) CRYPTO 2022. LNCS, vol. 13507, pp. 323–352. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-15802-5_12
Ghosh, S., Nilges, T.: An algebraic approach to maliciously secure private set intersection. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part III. LNCS, vol. 11478, pp. 154–185. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_6
Hazay, C., Lindell, Y.: Efficient protocols for set intersection and pattern matching with security against malicious and covert adversaries. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 155–175. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_10
Huang, Y., Evans, D., Katz, J.: Private set intersection: are garbled circuits better than custom protocols? In: NDSS 2012. The Internet Society, February 2012
Huberman, B.A., Franklin, M., Hogg, T.: Enhancing privacy and trust in electronic communities. In: ACM Conference On Electronic Commerce. ACM (1999)
Huberman, B.A., Franklin, M., Hogg, T.: Enhancing privacy and trust in electronic communities. In: Proceedings of the 1st ACM Conference on Electronic Commerce, pp. 78–86 (1999)
Ishai, Y., Kilian, J., Nissim, K., Petrank, E.: Extending oblivious transfers efficiently. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 145–161. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_9
Jarecki, S., Liu, X.: Fast secure computation of set intersection. In: Garay, J.A., De Prisco, R. (eds.) SCN 2010. LNCS, vol. 6280, pp. 418–435. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15317-4_26
Jawurek, M., Kerschbaum, F., Orlandi, C.: Zero-knowledge using garbled circuits: how to prove non-algebraic statements efficiently. In: Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) 2013 ACM SIGSAC Conference on Computer and Communications Security, CCS’13, Berlin, Germany, November 4–8, 2013, pp. 955–966. ACM (2013). https://doi.org/10.1145/2508859.2516662
Kissner, L., Song, D.: Privacy-preserving set operations. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 241–257. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_15
Kolesnikov, V., Kumaresan, R., Rosulek, M., Trieu, N.: Efficient batched oblivious PRF with applications to private set intersection. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S. (eds.) ACM CCS 2016, pp. 818–829. ACM Press, October 2016
Meadows, C.: A more efficient cryptographic matchmaking protocol for use in the absence of a continuously available third party. In: 1986 IEEE Symposium on Security and Privacy, pp. 134–134. IEEE (1986)
Pinkas, B., Rosulek, M., Trieu, N., Yanai, A.: SpOT-light: lightweight private set intersection from sparse OT extension. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part III. LNCS, vol. 11694, pp. 401–431. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_13
Pinkas, B., Rosulek, M., Trieu, N., Yanai, A.: PSI from PaXoS: fast, malicious private set intersection. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020, Part II. LNCS, vol. 12106, pp. 739–767. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45724-2_25
Pinkas, B., Schneider, T., Segev, G., Zohner, M.: Phasing: private set intersection using permutation-based hashing. In: Jung, J., Holz, T. (eds.) USENIX Security 2015, pp. 515–530. USENIX Association, August 2015
Pinkas, B., Schneider, T., Tkachenko, O., Yanai, A.: Efficient circuit-based PSI with linear communication. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part III. LNCS, vol. 11478, pp. 122–153. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_5
Pinkas, B., Schneider, T., Weinert, C., Wieder, U.: Efficient circuit-based PSI via cuckoo hashing. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part III. LNCS, vol. 10822, pp. 125–157. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_5
Pinkas, B., Schneider, T., Zohner, M.: Faster private set intersection based on OT extension. In: 23rd USENIX Security Symposium (USENIX Security 2014), pp. 797–812 (2014)
Rindal, P., Rosulek, M.: Improved private set intersection against malicious adversaries. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part I. LNCS, vol. 10210, pp. 235–259. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_9
Rindal, P., Rosulek, M.: Malicious-secure private set intersection via dual execution. In: Thuraisingham, B.M., Evans, D., Malkin, T., Xu, D. (eds.) ACM CCS 2017, pp. 1229–1242. ACM Press, October 2017
Rindal, P., Schoppmann, P.: VOLE-PSI: fast OPRF and circuit-PSI from vector-OLE. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021, Part II. LNCS, vol. 12697, pp. 901–930. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77886-6_31
Schoppmann, P., Gascón, A., Reichert, L., Raykova, M.: Distributed vector-OLE: improved constructions and implementation. In: Cavallaro, L., Kinder, J., Wang, X., Katz, J. (eds.) ACM CCS 2019, pp. 1055–1072. ACM Press, November 2019
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix
A Weak Boolean FSS Definition
Here we present the original weak boolean FSS formulation from [24] with no false positives.
Definition 14
(bFSS syntax). Let \(\mathcal {S} \subseteq 2^{\mathcal {U}}\) denote a family of sets over input domain \(\mathcal {U} \), security parameter \(\kappa \). A 2-party \(\rho \)-bFSS scheme with algorithms (Share, Eval) has the following syntax:
-
\((k_0,k_1)\leftarrow \textsf {Share} (1^\kappa ,S)\): is an algorithm with input the security parameter and (the description of) a set \(S \in \mathcal {S} \) and it outputs key shares \((k_0, k_1)\).
-
\(y_\textsf {idx} \leftarrow \textsf {Eval} (1^\kappa ,\textsf {idx},k_\textsf {idx},x)\): is a deterministic algorithm with input security parameter \(\kappa \), party index \(\textsf {idx} \in \{0,1\}\), key share \(k_\textsf {idx} \) and any \(x \in \mathcal {U} \). It outputs a binary string \(y_\textsf {idx} \) of length \(\rho \).
Definition 15
(bFSS security). A 2-party \(\rho \)-bFSS scheme \((\textsf {Share},\textsf {Eval})\) for \(\mathcal {S} \subseteq 2^{\mathcal {U}}\) is secure if is satisfies the following conditions:
-
Correctness for yes-instances: For every \(S \in \mathcal {S} \), \(x \in S\):
$$ \Pr \left( y_0 \oplus y_1 = 0^{\rho } \ \left| \begin{array}{l} (k_0,k_1) \leftarrow \textsf {Share} (1^\kappa ,S) \\ y_0 \leftarrow \textsf {Eval} (1^\kappa ,0,k_0,x) \\ y_1 \leftarrow \textsf {Eval} (1^\kappa ,1,k_1,x) \end{array}\right) \right. = 1 $$ -
Correctness for no-instances: For every set \(S \in \mathcal {S} \), \(x \in \mathcal {U} {\setminus } S\):
$$ \Pr \left( y_0 \oplus y_1 \ne 0^{\rho } \ \left| \begin{array}{l} (k_0,k_1) \leftarrow \textsf {Share} (1^\kappa ,S) \\ y_0 \leftarrow \textsf {Eval} (1^\kappa ,0,k_0,x) \\ y_1 \leftarrow \textsf {Eval} (1^\kappa ,1,k_1,x) \end{array}\right) \right. = 1 $$ -
Privacy: For every set \(S \in \mathcal {S} \) and index \(\textsf {idx} \in \{0,1\}\) there exists a simulator Sim such that the following distributions are computationally indistinguishable in the security parameter:
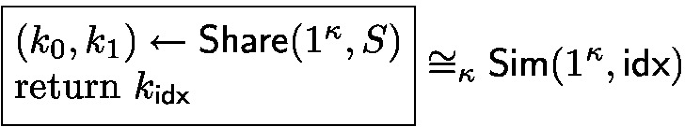
B dFSS Proofs/Constructions
1.1 B.1 dFSS for Singleton Sets, Intervals and a d-Dimensional Ball
The construction for the following theorem can be found in Fig. 11.
Theorem 2. Given a strong \(\rho \)-bFSS construction for singleton sets, 1-dimensional interval and d dimensional intervals with an invertible Share function, there exists a corresponding \(\rho \)-dFSS for \(\{ \textsf {PT} _{u,d}, \textsf {INT} _{\delta ,u}, \textsf {BALL} _{\delta ,u,d} \}\).
Proof
We’ll show how this theorem holds for the class of point functions, but a similar proof would follow for the other two collections as well.
To encode collection of point functions, we define its encoding group \(\mathbb {G} _{\textsf {PT}}\) as \([2^{ud}+1]\). The group element \(2^{ud}\) would encode the null set. Which helps us define the Encode function as follows:
Furthermore, we can define \(\textsf {Encode} ^{-1}_\textsf {PT} \) using the inverse of map. The proposed construction is presented in Fig. 11. Here the RShare outputs keys for a random singleton set, which is later derandomized in DEval to a chosen element by using an appropriate offset. Note, here we can encode a null set as well, by making the offset derandomize the singleton set to \(\{ 2^{ud}\}\) - which is outside the domain of the dFSS. Next we show how each of the dFSS properties are satisfied (Fig. 12).
-
Correctness: For any \(x,x^* \in PT_{u,d}\), and offset \(\textsf {offset} = \textsf {Encode} _\textsf {PT} (x^*)-r\), define \(y_\textsf {idx} \) to be \(F{.}\textsf {Eval} (1^\kappa ,\textsf {idx},k,\textsf {map} (x)-\textsf {offset})\). Then \(y_0 \oplus y_1 = 1 \iff \textsf {map} (x)=\textsf {map} (x^*)\) by the correctness of the underlying bFSS scheme, and else \(y_0 \oplus y_1 = 1\).
If the underlying bFSS has a correctness error - in the sense that the keys \(k_0,k_1\) evaluate to a null set with negligible probability, then the dFSS would give incorrect output for the element \(x^*\) if its not \(\emptyset \). This leads to a negligible error for a yes-instance of this dFSS. This negligible error does arise in point function constructions in [3, 8], which we’ll assume in this work.
For a no-instance of this dFSS, there is never any error in the output. Since the output \(y_0\oplus y_1\) is always zero when input \(x \ne x^*\).
-
Security: This follows directly from the privacy of the underlying bFSS, and by the fact that r acts as a one-time in the offset \(\textsf {Encode} (x^*)-r\).
-
Extractability: The Extract functions outputs the secret shared singleton element r, given the two keys \(k_0,k_1\). It can be constructed using the invertible Share function as follows:
$$ \textsf {Extract} (k_0,k_1) = \textsf {Encode} (\textsf {Share} ^{-1}(1^\kappa ,k_0,k_1)) $$
Similarly a bFSS for 1 dimensional interval and d dimensional fixed radius \(\ell _\infty \) can give us a corresponding dFSS by “reducing the domain size” to ensure a null set can be encoded by a set outside the specified domain of dFSS.
1.2 B.2 bFSS from dFSS
Theorem 6. Given a \(\rho \)-dFSS for \(\mathcal {S} \) with share size \(\sigma \), there exists a corresponding \(\rho \)-bFSS construction for \(\mathcal {S} \) with share size \(\sigma \).
Proof
Note that each of these Encode function are efficiently invertible. The \(\textsf {RShare},\textsf {DEval} \) for all these collections have the same structure, depicted in Fig. 11.
-
Correctness: The term \(\sum _{\textsf {idx} \in \{0,1\}} \) \(\textsf {Eval} (\textsf {idx},(k_\textsf {idx},\textsf {Encode} (S)-R),x) = \) \(\sum _{\textsf {idx} \in \{0,1\}}\) \(\textsf {Eval} (\textsf {idx},k_\textsf {idx},\textsf {Encode} (S)-R,x) \). Hence this follows directly from the correctness definition of dFSS.
-
Security: The simulator for the bFSS simply runs the simulator for the dFSS.
1.3 B.3 concat
Theorem 7. Given \(\rho _1\)-dFSS \(F_1\) for \(\mathcal {S} _1\) with share size \(\sigma _1\) and \(\rho _2\)-dFSS \(F_2\) for \(\mathcal {S} _2\) with share size \(\sigma _2\), there exists a \(\rho _1+\rho _2\)-dFSS \(\textsf {concat} [F_1,F_2]\) for \(\mathcal {S} _1 \times \mathcal {S} _2\) with share size \(\sigma _1+\sigma _2\). Furthermore, if \(F_1\) and \(F_2\) dFSS have pseduo-random keys, then so does \(\textsf {concat} [F_1,F_2]\).
Proof
Given encode functions \(\textsf {Encode} _1: \mathcal {S} _1 \rightarrow \mathbb {G} _1\) and \(\textsf {Encode} _2: \mathcal {S} _2 \rightarrow \mathbb {G} _2\) for dFSS \(F_1\) and \(F_2\) respectively, we define encode function for concat [\(F_1,F_2\)] \(\textsf {Encode}: \mathcal {S} _1 \times \mathcal {S} _2 \rightarrow \mathbb {G} _1 \times \mathbb {G} _2\) as:
Note that this Encode function is efficiently invertible if the two component Encode functions are. Encodings with respect to the new Encode function form a group which is a direct product of the groups for the component FSS.
-
Correctness: The correctness of \(F=\textsf {concat} [F_1,F_2]\) reduces to the correctness of \(F_1\) and \(F_2\). The first \(k_1\) bits of the term \(y=\sum _{\textsf {idx} \in \{0,1\}}\) \(F.\textsf {DEval} (\textsf {idx},(k_\textsf {idx} \) \(,\textsf {Encode} (S_1,S_2)-(R_1,R_2)),(x,y)) \) equal \(\sum _{\textsf {idx} \in \{0,1\}}\) \(F_1{.}\textsf {Eval} (\textsf {idx},(k_\textsf {idx},\textsf {Encode} (S_1)-R_1),x) \) and the last \(k_2\) bit of y equal \(\sum _{\textsf {idx} \in \{0,1\}}\) \(F_2{.}\textsf {Eval} (\textsf {idx},(k_\textsf {idx},\textsf {Encode} (S_2)-R_2),x) \). Hence, \(y=0^{k_1+k_2}\) for \((x,y) \in S_1 \times S_2\). And if \(x \not \in S_1\), the first \({k_1}\) bits are not all zero bits with probability at least \(p_1\), and if \(x \not \in S_2\), the last \({k_2}\) bits are not all zero bits with probability at least \(p_2\).
-
Security: The simulator \(\textsf {Sim} \) for \(\textsf {concat} [F_1,F_2]\) invokes the simulators for \(F_1\) and \(F_2\), which output \((k_0,\textsf {offset} _0)\) and \((k_1,\textsf {offset} _1)\). Then \(\textsf {Sim} \) outputs \(((k_0,k_1),(\textsf {offset} _0,\textsf {offset} _1))\).
-
Extractability: This is reduced to the extractability property of the two underlying dFSS \(F_1\) and \(F_2\) as shown in Fig. 13.
Rights and permissions
Copyright information
© 2023 International Association for Cryptologic Research
About this paper
Cite this paper
Garimella, G., Rosulek, M., Singh, J. (2023). Malicious Secure, Structure-Aware Private Set Intersection. In: Handschuh, H., Lysyanskaya, A. (eds) Advances in Cryptology – CRYPTO 2023. CRYPTO 2023. Lecture Notes in Computer Science, vol 14081. Springer, Cham. https://doi.org/10.1007/978-3-031-38557-5_19
Download citation
DOI: https://doi.org/10.1007/978-3-031-38557-5_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-38556-8
Online ISBN: 978-3-031-38557-5
eBook Packages: Computer ScienceComputer Science (R0)