Abstract
We address the fundamental problem of computing range functions
 for a real function \(f:\mathbb {R}\rightarrow \mathbb {R}\). In our previous work [9], we introduced recursive interpolation range functions based on the Cornelius–Lohner (CL) framework of decomposing f as \(f=g+R\), which requires to compute g(I) “exactly” for an interval I. There are two problems: this approach limits the order of convergence to 6 in practice, and exact computation is impossible to achieve in standard implementation models. We generalize the CL framework by allowing g(I) to be approximated by strong range functions
for a real function \(f:\mathbb {R}\rightarrow \mathbb {R}\). In our previous work [9], we introduced recursive interpolation range functions based on the Cornelius–Lohner (CL) framework of decomposing f as \(f=g+R\), which requires to compute g(I) “exactly” for an interval I. There are two problems: this approach limits the order of convergence to 6 in practice, and exact computation is impossible to achieve in standard implementation models. We generalize the CL framework by allowing g(I) to be approximated by strong range functions
 , where \(\varepsilon >0\) is a user-specified bound on the error. This new framework allows, for the first time, the design of interval forms for f with any desired order of convergence. To achieve our strong range functions, we generalize Neumaier’s theory of constructing range functions from expressions over a Lipschitz class \(\varOmega \) of primitive functions. We show that the class \(\varOmega \) is very extensive and includes all common hypergeometric functions. Traditional complexity analysis of range functions is based on individual evaluation on an interval. Such analysis cannot differentiate between our novel recursive range functions and classical Taylor-type range functions. Empirically, our recursive functions are superior in the “holistic” context of the root isolation algorithm Eval. We now formalize this holistic approach by defining the amortized complexity of range functions over a subdivision tree. Our theoretical model agrees remarkably well with the empirical results. Among our previous novel range functions, we identified a Lagrange-type range function
, where \(\varepsilon >0\) is a user-specified bound on the error. This new framework allows, for the first time, the design of interval forms for f with any desired order of convergence. To achieve our strong range functions, we generalize Neumaier’s theory of constructing range functions from expressions over a Lipschitz class \(\varOmega \) of primitive functions. We show that the class \(\varOmega \) is very extensive and includes all common hypergeometric functions. Traditional complexity analysis of range functions is based on individual evaluation on an interval. Such analysis cannot differentiate between our novel recursive range functions and classical Taylor-type range functions. Empirically, our recursive functions are superior in the “holistic” context of the root isolation algorithm Eval. We now formalize this holistic approach by defining the amortized complexity of range functions over a subdivision tree. Our theoretical model agrees remarkably well with the empirical results. Among our previous novel range functions, we identified a Lagrange-type range function
 as the overall winner. In this paper, we introduce a Hermite-type range function
as the overall winner. In this paper, we introduce a Hermite-type range function
 that is even better. We further explore speeding up applications by choosing non-maximal recursion levels.
that is even better. We further explore speeding up applications by choosing non-maximal recursion levels.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Definitions of our terminology are collected in Sect. 1.3.
- 2.
The appearance of sqr may be curious, but that is because he will later define interval forms of the operations in \(\varOmega \).
- 3.
Each
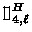 is an operator that transforms any sufficiently smooth function \(f:\mathbb {R}\rightarrow \mathbb {R}\) into the range function
is an operator that transforms any sufficiently smooth function \(f:\mathbb {R}\rightarrow \mathbb {R}\) into the range function
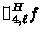 for f.
for f. - 4.
The concept of a function f (not expression) being Lipschitz on a set U is standard: it means that there exists a vector \(\boldsymbol{\ell }=(\ell _1,\dots ,\ell _m)\) of positive constants, such that for all \(\boldsymbol{x},\boldsymbol{y}\in U\subseteq \mathbb {R}^m\), \(|f(\boldsymbol{x})-f(\boldsymbol{y})|\le \boldsymbol{\ell }*|\boldsymbol{x}-\boldsymbol{y}|\) where \(*\) is the dot product and \(|\boldsymbol{x}-\boldsymbol{y}|=(|x_1-y_1|,\dots ,|x_m-y_m|)\). Call \(\boldsymbol{\ell }\) a Lipschitz constant vector for U.
- 5.
Note that in our Eval application, we must simultaneously evaluate
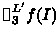 as well as its derivative
as well as its derivative
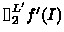 . But it turns out that we can bound the range of \(f'\) for no additional evaluation cost.
. But it turns out that we can bound the range of \(f'\) for no additional evaluation cost. - 6.
If d is not divisible by 3, we can ensure a total cost of d evaluations per interval of the tree but the tree shape will dictate how to distribute these evaluations on the \(m+1\) nodes.
- 7.
The notation “\(C_d^h(n)\)” does not fully reproduce the previous notations of \(C^L_3(n)\) and \(C^H_4(n)\) (which were chosen to be consistent with
 and
and
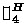 ). Also, d is implicit in the previous notations.
). Also, d is implicit in the previous notations. - 8.
This is a notational shift from our previous paper, where we indexed the recursion level by \(n\ge 1\). Thus, level \(\ell \) in this paper corresponds to \(n-1\) in the old notation.
References
Burr, M., Krahmer, F.: SqFreeEVAL: an (almost) optimal real-root isolation algorithm. J. Symb. Comput. 47(2), 153–166 (2012)
Core Library homepage: Software download, source, documentation and links (1999). https://cs.nyu.edu/exact/core_pages/svn-core.html
Cornelius, H., Lohner, R.: Computing the range of values of real functions with accuracy higher than second order. Computing 33(3), 331–347 (1984)
Du, Z., Eleftheriou, M., Moreira, J., Yap, C.: Hypergeometric functions in exact geometric computation. In: Brattka, V., Schoeder, M., Weihrauch, K. (eds.) Proceedings of 5th Workshop on Computability and Complexity in Analysis, pp. 55–66 (2002)
Du, Z., Yap, C.: Uniform complexity of approximating hypergeometric functions with absolute error. In: Pae, S., Park, H. (eds.) Proceedings of 7th Asian Symposium on Computer Math, pp. 246–249 (2006)
Fousse, L., Hanrot, G., Lefèvre, V., Pélissier, P., Zimmermann, P.: MPFR: a multiple-precision binary floating-point library with correct rounding. ACM Trans. Math. Softw. 33(2), Article 13, 15 (2007). https://www.mpfr.org
Granlund, T.: The GMP development team: GNU MP: The GNU Multiple Precision Arithmetic Library, 6.2.1. edn. (2020). https://gmplib.org/
Higham, N.J.: Accuracy and Stability of Numerical Algorithms, 2nd edn. Society for Industrial and Applied Mathematics, Philadelphia (2002)
Hormann, K., Kania, L., Yap, C.: Novel range functions via taylor expansions and recursive lagrange interpolation with application to real root isolation. In: International Symposium Symbolic and Algebraic Comp. (46th ISSAC), pp. 193–200 (2021)
Johansson, F.: Computing hypergeometric functions rigorously. ACM Trans. Math. Softw. 45(3), 1–26 (2019)
Neumaier, A.: Interval Methods for Systems of Equations. Cambridge University Press, Cambridge (1990)
Ratschek, H.: Centered forms. SIAM J. Num. Anal. 17(5), 656–662 (1980)
Ratschek, H., Rokne, J.: Computer Methods for the Range of Functions. Horwood Publishing Limited, Chichester (1984)
Revol, N., Rouillier, F.: Motivations for an arbitrary precision interval arithmetic and the MPFI library. Reliable Comput. 11(4), 275–290 (2005). https://gitlab.inria.fr/mpfi/mpfi
Shadrin, A.: Error bounds for Lagrange interpolation. J. Approx. Theory 80(1), 25–49 (1995)
Sharma, V., Yap, C.: Near optimal tree size bounds on a simple real root isolation algorithm. In: 37th International Symposium Symbolic and Algebraic Computation (ISSAC 2012), pp. 319–326 (2012)
Trefethen, L.N., Bau, D.: Numerical Linear Algebra. Society for Industrial and Applied Mathematics, Philadelphia (1997)
Waldron, S.F.: \(L_p\)-error bounds for Hermite interpolation and the associated Wirtinger inequalities. J. Constr. Approx. 13(4), 461–479 (1997)
Xu, J., Yap, C.: Effective subdivision algorithm for isolating zeros of real systems of equations, with complexity analysis. In: International Symposium Symbolic and Algebraic Computation (44th ISSAC), pp. 355–362 (2019)
Yap, C.K.: On guaranteed accuracy computation. In: Chen, F., Wang, D. (eds.) Geometric Computation, Chap. 12, pp. 322–373. World Scientific Publishing Co., Singapore (2004)
Yu, J., Yap, C., Du, Z., Pion, S., Brönnimann, H.: The design of core 2: a library for exact numeric computation in geometry and algebra. In: Fukuda, K., Hoeven, J., Joswig, M., Takayama, N. (eds.) ICMS 2010. LNCS, vol. 6327, pp. 121–141. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15582-6_24
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Hormann, K., Yap, C., Zhang, Y.S. (2023). Range Functions of Any Convergence Order and Their Amortized Complexity Analysis. In: Boulier, F., England, M., Kotsireas, I., Sadykov, T.M., Vorozhtsov, E.V. (eds) Computer Algebra in Scientific Computing. CASC 2023. Lecture Notes in Computer Science, vol 14139. Springer, Cham. https://doi.org/10.1007/978-3-031-41724-5_9
Download citation
DOI: https://doi.org/10.1007/978-3-031-41724-5_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-41723-8
Online ISBN: 978-3-031-41724-5
eBook Packages: Computer ScienceComputer Science (R0)





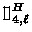 is an operator that transforms any sufficiently smooth function
is an operator that transforms any sufficiently smooth function 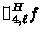 for f.
for f.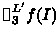 as well as its derivative
as well as its derivative
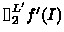 . But it turns out that we can bound the range of
. But it turns out that we can bound the range of  and
and
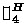 ). Also, d is implicit in the previous notations.
). Also, d is implicit in the previous notations.