A New Width Parameter of Graphs Based on Edge Cuts: $\alpha$-Edge-Crossing Width

Abstract

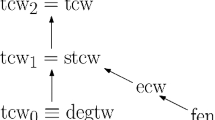
We introduce graph width parameters, called $\alpha$-edge-crossing width and edge-crossing width. These are defined in terms of the number of edges crossing a bag of a tree-cut decomposition. They are motivated by edge-cut width, recently introduced by Brand et al. (WG 2022). We show that edge-crossing width is equivalent to the known parameter tree-partition-width. On the other hand, $\alpha$-edge-crossing width is a new parameter; tree-cut width and $\alpha$-edge-crossing width are incomparable, and they both lie between tree-partition-width and edge-cut width.

We provide an algorithm that, for a given n-vertex graph G and integers k and $\alpha$, in time $2^{O((\alpha +k)\log (\alpha +k))}n^2$ either outputs a tree-cut decomposition certifying that the $\alpha$-edge-crossing width of G is at most $2\alpha ^2+5k$ or confirms that the $\alpha$-edge-crossing width of G is more than k. As applications, for every fixed $\alpha$, we obtain FPT algorithms for the List Coloring and Precoloring Extension problems parameterized by $\alpha$-edge-crossing width. They were known to be W[1]-hard parameterized by tree-partition-width, and FPT parameterized by edge-cut width, and we close the complexity gap between these two parameters.

A full version of the paper is available at https://arxiv.org/abs/2302.04624.

Y. Chang, O. Kwon, and M. Lee are supported by the National Research Foundation of Korea (NRF) grant funded by the Ministry of Science and ICT (No. NRF-2021K2A9A2A11101617 and RS-2023-00211670). O. Kwon is also supported by Institute for Basic Science (IBS-R029-C1).