Abstract
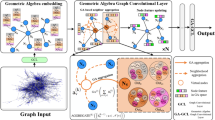
Recent research has shown that alignment between the structure of graph data and the geometry of an embedding space is crucial for learning high-quality representations of the data. The uniform geometry of Euclidean and hyperbolic spaces allows for representing graphs with uniform geometric and topological features, such as grids and hierarchies, with minimal distortion. However, real-world graph data is characterized by multiple types of geometric and topological features, necessitating more sophisticated geometric embedding spaces. In this work, we utilize the Riemannian symmetric space of symmetric positive definite matrices (\({\text {SPD}}\)) to construct graph neural networks that can robustly handle complex graphs. To do this, we develop an innovative library that leverages the \({\text {SPD}}\) gyrocalculus tools [26] to implement the building blocks of five popular graph neural networks in \({\text {SPD}}\). Experimental results demonstrate that our graph neural networks in \({\text {SPD}}\) substantially outperform their counterparts in Euclidean and hyperbolic spaces, as well as the Cartesian product thereof, on complex graphs for node and graph classification tasks. We release the library and datasets at https://github.com/andyweizhao/SPD4GNNs.
F. Lopez and D. Taha—These authors contributed equally to this work.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
TgReEig equals ReEig in the case of \(\varphi _a(x) = \max (x, 1)\).
- 2.
For graph classification, \(Z_i\) and \(y_i\) denote the ‘center’ of the graph i and its true class. We take the arithmetic mean of node embeddings in \({\text {SPD}}_n\) to produce \(Z_i \in {\text {SPD}}_n\).
- 3.
We also design several classifiers with the input space in \({\text {SPD}}_n\), but these do not yield better results than those in \(S_n\).
References
Anderson, R.M., May, R.M.: Infectious Diseases of Humans: Dynamics and Control. Oxford University Press, Oxford (1992)
Barcelo, P., Galkin, M., Morris, C., Orth, M.R.: Weisfeiler and leman go relational. In: The First Learning on Graphs Conference (2022). https://openreview.net/forum?id=wY_IYhh6pqj
Borgwardt, K.M., Ong, C.S., Schönauer, S., Vishwanathan, S., Smola, A.J., Kriegel, H.P.: Protein function prediction via graph kernels. Bioinformatics 21(suppl_1), i47–i56 (2005)
Bronstein, M.M., Bruna, J., LeCun, Y., Szlam, A., Vandergheynst, P.: Geometric deep learning: going beyond euclidean data. IEEE Signal Process. Mag. 34(4), 18–42 (2017)
Brooks, D., Schwander, O., Barbaresco, F., Schneider, J.Y., Cord, M.: Riemannian batch normalization for SPD neural networks. In: Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R. (eds.) Advances in Neural Information Processing Systems, vol. 32, pp. 15489–15500. Curran Associates, Inc. (2019). https://proceedings.neurips.cc/paper/2019/file/6e69ebbfad976d4637bb4b39de261bf7-Paper.pdf
Brooks, D.A., Schwander, O., Barbaresco, F., Schneider, J.Y., Cord, M.: Exploring complex time-series representations for Riemannian machine learning of radar data. In: ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 3672–3676 (2019). https://doi.org/10.1109/ICASSP.2019.8683056
Buyalo, S., Schroeder, V.: Embedding of hyperbolic spaces in the product of trees. Geom. Dedicata. 113(1), 75–93 (2005)
Cannon, J.W., Floyd, W.J., Kenyon, R., Parry, W.R., et al.: Hyperbolic geometry. Flavors Geom. 31(59–115), 2 (1997)
Chakraborty, R., Bouza, J., Manton, J., Vemuri, B.C.: ManifoldNet: A deep neural network for manifold-valued data with applications. IEEE Trans. Pattern Anal. Mach. Intell., 1 (2020). https://doi.org/10.1109/TPAMI.2020.3003846
Chakraborty, R., et al.: A statistical recurrent model on the manifold of symmetric positive definite matrices. In: Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R. (eds.) Advances in Neural Information Processing Systems, vol. 31. Curran Associates, Inc. (2018). https://proceedings.neurips.cc/paper/2018/file/7070f9088e456682f0f84f815ebda761-Paper.pdf
Chami, I., Ying, Z., Ré, C., Leskovec, J.: Hyperbolic graph convolutional neural networks. In: Advances in Neural Information Processing Systems, vol. 32, pp. 4869–4880. Curran Associates, Inc. (2019). https://proceedings.neurips.cc/paper/2019/file/0415740eaa4d9decbc8da001d3fd805f-Paper.pdf
Defferrard, M., Bresson, X., Vandergheynst, P.: Convolutional neural networks on graphs with fast localized spectral filtering. In: Advances in Neural Information Processing Systems, vol. 29 (2016)
Defferrard, M., Milani, M., Gusset, F., Perraudin, N.: DeepSphere: a graph-based spherical CNN. In: International Conference on Learning Representations (2020). https://openreview.net/forum?id=B1e3OlStPB
Di Giovanni, F., Rowbottom, J., Chamberlain, B.P., Markovich, T., Bronstein, M.M.: Graph neural networks as gradient flows. arXiv preprint: arXiv:2206.10991 (2022)
Dong, Z., Jia, S., Zhang, C., Pei, M., Wu, Y.: Deep manifold learning of symmetric positive definite matrices with application to face recognition. In: Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, AAAI’17, pp. 4009–4015. AAAI Press (2017)
Eliasof, M., Haber, E., Treister, E.: PDE-GCN: novel architectures for graph neural networks motivated by partial differential equations. In: Advances in Neural Information Processing Systems, vol. 34, pp. 3836–3849 (2021)
Gao, Z., Wu, Y., Bu, X., Yu, T., Yuan, J., Jia, Y.: Learning a robust representation via a deep network on symmetric positive definite manifolds. Pattern Recogn. 92, 1–12 (2019). https://doi.org/10.1016/j.patcog.2019.03.007, https://www.sciencedirect.com/science/article/pii/S0031320319301062
Gu, A., Sala, F., Gunel, B., Ré, C.: Learning mixed-curvature representations in product spaces. In: International Conference on Learning Representations (2019). https://openreview.net/forum?id=HJxeWnCcF7
Hamilton, W., Ying, Z., Leskovec, J.: Inductive representation learning on large graphs. In: Guyon, I., et al. (eds.) Advances in Neural Information Processing Systems, vol. 30. Curran Associates, Inc. (2017). https://proceedings.neurips.cc/paper/2017/file/5dd9db5e033da9c6fb5ba83c7a7ebea9-Paper.pdf
Helgason, S.: Differential Geometry, Lie Groups, and Symmetric Spaces. Academic Press, New York (1978)
Huang, Z., Van Gool, L.: A Riemannian network for SPD matrix learning. In: Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, AAAI’17, pp. 2036–2042. AAAI Press (2017)
Kipf, T.N., Welling, M.: Semi-supervised classification with graph convolutional networks. In: 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, 24–26 April 2017. Conference Track Proceedings (2017). https://openreview.net/forum?id=SJU4ayYgl
Krioukov, D., Papadopoulos, F., Kitsak, M., Vahdat, A., Boguná, M.: Hyperbolic geometry of complex networks. Phys. Rev. E 82(3), 036106 (2010)
Liu, Q., Nickel, M., Kiela, D.: Hyperbolic graph neural networks. In: Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R. (eds.) Advances in Neural Information Processing Systems, vol. 32. Curran Associates, Inc. (2019)
López, F., Pozzetti, B., Trettel, S., Strube, M., Wienhard, A.: Symmetric spaces for graph embeddings: a finsler-riemannian approach. In: Meila, M., Zhang, T. (eds.) Proceedings of the 38th International Conference on Machine Learning. Proceedings of Machine Learning Research, vol. 139, pp. 7090–7101. PMLR (2021). https://proceedings.mlr.press/v139/lopez21a.html
López, F., Pozzetti, B., Trettel, S., Strube, M., Wienhard, A.: Vector-valued distance and gyrocalculus on the space of symmetric positive definite matrices. In: Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M.F., Lin, H. (eds.) Advances in Neural Information Processing Systems, vol. 34. Curran Associates, Inc. (2021)
Morris, C., Kriege, N.M., Bause, F., Kersting, K., Mutzel, P., Neumann, M.: TUDataset: a collection of benchmark datasets for learning with graphs. In: ICML 2020 Workshop on Graph Representation Learning and Beyond (GRL+ 2020) (2020). https://www.graphlearning.io
Namata, G., London, B., Getoor, L., Huang, B., Edu, U.: Query-driven active surveying for collective classification. In: 10th International Workshop on Mining and Learning with Graphs, vol. 8, p. 1 (2012)
Nguyen, X.S., Brun, L., Lezoray, O., Bougleux, S.: A neural network based on SPD manifold learning for skeleton-based hand gesture recognition. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (2019)
Riesen, K., Bunke, H.: IAM graph database repository for graph based pattern recognition and machine learning. In: da Vitoria Lobo, N., et al. (eds.) SSPR /SPR 2008. LNCS, vol. 5342, pp. 287–297. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89689-0_33
Rusch, T.K., Chamberlain, B., Rowbottom, J., Mishra, S., Bronstein, M.: Graph-coupled oscillator networks. In: International Conference on Machine Learning, pp. 18888–18909. PMLR (2022)
Satorras, V.G., Hoogeboom, E., Welling, M.: E (n) equivariant graph neural networks. In: International Conference on Machine Learning, pp. 9323–9332. PMLR (2021)
Schomburg, I., et al.: BRENDA, the enzyme database: updates and major new developments. Nucleic Acids Res. 32(suppl_1), D431–D433 (2004)
Sen, P., Namata, G., Bilgic, M., Getoor, L., Galligher, B., Eliassi-Rad, T.: Collective classification in network data. AI Mag. 29(3), 93 (2008)
Sonthalia, R., Gilbert, A.: Tree! i am no tree! i am a low dimensional hyperbolic embedding. In: Advances in Neural Information Processing Systems, vol. 33, pp. 845–856 (2020)
Sutherland, J.J., O’brien, L.A., Weaver, D.F.: Spline-fitting with a genetic algorithm: a method for developing classification structure- activity relationships. J. Chem. Inf. Comput. Sci. 43(6), 1906–1915 (2003)
Veličković, P., Cucurull, G., Casanova, A., Romero, A., Lió, P., Bengio, Y.: Graph attention networks. In: International Conference on Learning Representations (2018). https://openreview.net/forum?id=rJXMpikCZ
Wu, F., Souza, A., Zhang, T., Fifty, C., Yu, T., Weinberger, K.: Simplifying graph convolutional networks. In: International Conference on Machine Learning, pp. 6861–6871. PMLR (2019)
Xu, K., Hu, W., Leskovec, J., Jegelka, S.: How powerful are graph neural networks? In: 7th International Conference on Learning Representations, ICLR 2019, New Orleans, LA, USA, 6–9 May 2019. OpenReview.net (2019). https://openreview.net/forum?id=ryGs6iA5Km
Yu, T., De Sa, C.: HyLa: hyperbolic Laplacian features for graph learning. arXiv preprint: arXiv:2202.06854 (2022)
Zhang, M., Chen, Y.: Link prediction based on graph neural networks. In: Advances in Neural Information Processing Systems, vol. 31 (2018)
Zhang, T., Zheng, W., Cui, Z., Li, C.: Deep manifold-to-manifold transforming network. In: 2018 25th IEEE International Conference on Image Processing (ICIP), pp. 4098–4102 (2018). DOI: https://doi.org/10.1109/ICIP.2018.8451626
Acknowledgements
We thank Anna Wienhard and Maria Beatrice Pozetti for insightful discussions, as well as the anonymous reviewers for their thoughtful feedback that greatly improved the texts. This work has been supported by the Klaus Tschira Foundation, Heidelberg, Germany, as well as under Germany’s Excellence Strategy EXC-2181/1 - 390900948 (the Heidelberg STRUCTURES Cluster of Excellence).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Ethics declarations
Ethical Considerations
We have not identified any immediate ethical concerns such as bias and discrimination, misinformation dissemination, privacy issues, originating from the contributions presented in this work. However, it is important to note that our \({\text {SPD}}\) models use computationally demanding functions, such as determining eigenvalues and eigenvectors, which may incur a negative environmental impact due to increased energy consumption. Nevertheless, SPD models do not outsuffer Euclidean and hyperbolic counterparts in terms of computational overhead. This is because Euclidean and hyperbolic models would require substantial computing resources when dealing with larger dimensions, a necessity for compensating for the challenges of embedding complex graphs into these ill-suited spaces.
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Zhao, W., Lopez, F., Riestenberg, J.M., Strube, M., Taha, D., Trettel, S. (2023). Modeling Graphs Beyond Hyperbolic: Graph Neural Networks in Symmetric Positive Definite Matrices. In: Koutra, D., Plant, C., Gomez Rodriguez, M., Baralis, E., Bonchi, F. (eds) Machine Learning and Knowledge Discovery in Databases: Research Track. ECML PKDD 2023. Lecture Notes in Computer Science(), vol 14171. Springer, Cham. https://doi.org/10.1007/978-3-031-43418-1_8
Download citation
DOI: https://doi.org/10.1007/978-3-031-43418-1_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-43417-4
Online ISBN: 978-3-031-43418-1
eBook Packages: Computer ScienceComputer Science (R0)