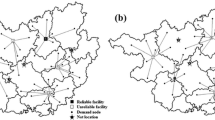
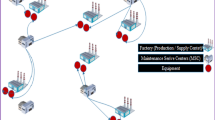
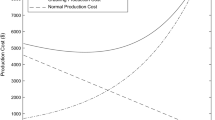
Abstract
Supply chain resilience is one of the most relevant topics of operations research and production management, which is aimed to risk mitigation in the global manufacturing, logistics, and trade. Conventional approach for resilient supply chain design involves the stochastic modeling and scenery-based description of anticipated failures in transportation networks. However, the stochastic approach can be insufficiently adequate in a situation of an unexpected failure or interruption. In this paper, we introduce the Reliable Production Process Design Problem (RPPDP), where the goal is to guarantee a suitable behaviour of the given highly distributed manufacturing system with respect to an (almost) arbitrary potential failure. This problem appears to be strongly NP-hard, similarly to the famous Constrained Shortest Path Tour and Shortest Simple Path with t Must Pass Nodes combinatorial problems. In order to find (close to) optimal solutions of the problem in question efficiently, we propose a compact Mixed Integer Linear Program (MILP) model and an Adaptive Large Neighborhood Search (ALNS) based primal heuristic. Results of their extensive numerical evaluation on top of the Gurobi branching framework, against the instances derived from the PCGTSPLIB library show high performance of the proposed methods.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
de Andrade, R.C.: Elementary shortest-paths visiting a given set of nodes (2013). http://www.din.uem.br/sbpo/sbpo2013/pdf/arq0242.pdf
de Andrade, R.C.: New formulations for the elementary shortest-path problem visiting a given set of nodes. Eur. J. Oper. Res. 254(3), 755–768 (2016). https://doi.org/10.1016/j.ejor.2016.05.008
Balas, E., Fischetti, M., Pulleyblank, W.: The precedence-constraint asymmetric traveling salesman polytope. Math. Program. 68, 241–265 (1995). https://doi.org/10.1007/BF01585767
Balas, E., Simonetti, N.: Linear time dynamic-programming algorithms for new classes of restricted TSPs: a computational study. INFORMS J. Comput. 13(1), 56–75 (2001). https://doi.org/10.1287/ijoc.13.1.56.9748
Chentsov, A.G., Khachai, M.Y., Khachai, D.M.: An exact algorithm with linear complexity for a problem of visiting megalopolises. Proc. Steklov Inst. Math. 295(1), 38–46 (2016). https://doi.org/10.1134/S0081543816090054
Deng, C., Xiong, Y., Yang, L., Yang, Y.: A smoothing SAA method for solving a nonconvex multisource supply chain stochastic optimization model. Math. Probl. Eng. 2022 (2022). https://doi.org/10.1155/2022/5617213
Dewil, R., Vansteenwegen, P., Cattrysse, D.: A review of cutting path algorithms for laser cutters. Int. J. Adv. Manuf. Technol. 87(5), 1865–1884 (2016). https://doi.org/10.1007/s00170-016-8609-1
Fan, Y., Schwartz, F., Vob, S., Woodruff, D.L.: Catastrophe insurance and flexible planning for supply chain disruption management: a stochastic simulation case study. Int. J. Prod. Res. (2023). https://doi.org/10.1080/00207543.2023.2176179
Ferone, D., Festa, P., Guerriero, F.: An efficient exact approach for the constrained shortest path tour problem. Optim. Methods Softw. 35(1), 1–20 (2020). https://doi.org/10.1080/10556788.2018.1548015
Ferone, D., Festa, P., Guerriero, F., Laganà, D.: The constrained shortest path tour problem. Comput. Oper. Res. 74, 64–77 (2016). https://doi.org/10.1016/j.cor.2016.04.002
Gomes, T., Marques, S., Martins, L., Pascoal, M., Tipper, D.: Protected shortest path visiting specified nodes (2015). https://doi.org/10.1109/RNDM.2015.7325218
Gomes, T., Martins, L., Ferreira, S., Pascoal, M., Tipper, D.: Algorithms for determining a node-disjoint path pair visiting specified nodes. Opt. Switching Netw. 23 (2017). https://doi.org/10.1016/j.osn.2016.05.002
L. Gurobi Optimization: Gurobi optimizer reference manual (2021). https://www.gurobi.com/documentation/9.5/refman/index.html
Gutin, G., Punnen, A.P.: The Traveling Salesman Problem and Its Variations. Springer, Boston (2007)
Kalateh Ahani, I., Salari, M., Hosseini, S.M., Iori, M.: Solution of minimum spanning forest problems with reliability constraints. Comput. Ind. Eng. 142, 106365 (2020). https://doi.org/10.1016/j.cie.2020.106365
Karuppusamy, N.S., Kang, B.Y.: Minimizing airtime by optimizing tool path in computer numerical control machine tools with application of \(A^*\) and genetic algorithms. Adv. Mech. Eng. 9(12), 1687814017737448 (2017). https://doi.org/10.1177/1687814017737448
Khachai, D., Sadykov, R., Battaia, O., Khachay, M.: Precedence constrained generalized traveling salesman problem: polyhedral study, formulations, and branch-and-cut algorithm. Eur. J. Oper. Res. (2023). https://doi.org/10.1016/j.ejor.2023.01.039
Khachai, M.Y., Neznakhina, E.D.: Approximation schemes for the generalized traveling salesman problem. Proc. Steklov Inst. Math. 299(1), 97–105 (2017). https://doi.org/10.1134/S0081543817090127
Khachay, M., Kudriavtsev, A., Petunin, A.: PCGLNS: a heuristic solver for the precedence constrained generalized traveling salesman problem. In: Olenev, N., Evtushenko, Y., Khachay, M., Malkova, V. (eds.) OPTIMA 2020. LNCS, vol. 12422, pp. 196–208. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-62867-3_15
Khachay, M., Neznakhina, K.: Complexity and approximability of the Euclidean generalized traveling salesman problem in grid clusters. Ann. Math. Artif. Intell. 88(1), 53–69 (2020). https://doi.org/10.1007/s10472-019-09626-w
Kudriavtsev, A., et al.: The shortest simple path problem with a fixed number of must-pass nodes: a problem-specific branch-and-bound algorithm. In: Simos, D.E., Pardalos, P.M., Kotsireas, I.S. (eds.) LION 2021. LNCS, vol. 12931, pp. 198–210. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-92121-7_17
Martin, S., Magnouche, Y., Juvigny, C., Leguay, J.: Constrained shortest path tour problem: branch-and-price algorithm. Comput. Oper. Res. 144, 105819 (2022). https://doi.org/10.1016/j.cor.2022.105819
Morin, T.L., Marsten, R.E.: Branch-and-bound strategies for dynamic programming. Oper. Res. 24(4), 611–627 (1976)
Ogorodnikov, Y., Rudakov, R., Khachay, D., Khachay, M.: A problem-specific branch-and-bound algorithm for the protected shortest simple path problem with must-pass nodes. IFAC-PapersOnLine 55, 572–577 (2022). https://doi.org/10.1016/j.ifacol.2022.09.455
Papadimitriou, C.: Euclidean TSP is NP-complete. Theor. Comput. Sci. 4, 237–244 (1977)
Ropke, S., Pisinger, D.: An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows. Transp. Sci. 40, 455–472 (2006). https://doi.org/10.1287/trsc.1050.0135
Saksena, J.P., Kumar, S.: The routing problem with ‘k’ specified nodes. Oper. Res. 14(5), 909–913 (1966)
Salman, R., Carlson, J.S., Ekstedt, F., Spensieri, D., Torstensson, J., Söderberg, R.: An industrially validated CMM inspection process with sequence constraints. Procedia CIRP 44, 138–143 (2016). https://doi.org/10.1016/j.procir.2016.02.136
Salman, R., Ekstedt, F., Damaschke, P.: Branch-and-bound for the precedence constrained generalized traveling salesman problem. Oper. Res. Lett. 48(2), 163–166 (2020). https://doi.org/10.1016/j.orl.2020.01.009
Schilling, L., Seuring, S.: Linking the digital and sustainable transformation with supply chain practices. Int. J. Prod. Res. 1–25 (2023). https://doi.org/10.1080/00207543.2023.2173502
Smith, S.L., Imeson, F.: GLNS: an effective large neighborhood search heuristic for the generalized traveling salesman problem. Comput. Oper. Res. 87, 1–19 (2017). https://doi.org/10.1016/j.cor.2017.05.010
Acknowledgements
The work was performed as part of research carried out in the Ural Mathematical Center with the financial support of the Ministry of Science and Higher Education of the Russian Federation (Agreement number 075-02-2023-913).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Rudakov, R., Khachai, D., Ogorodnikov, Y., Khachay, M. (2023). Reliable Production Process Design Problem: Compact MILP Model and ALNS-Based Primal Heuristic. In: Olenev, N., Evtushenko, Y., Jaćimović, M., Khachay, M., Malkova, V. (eds) Optimization and Applications. OPTIMA 2023. Lecture Notes in Computer Science, vol 14395. Springer, Cham. https://doi.org/10.1007/978-3-031-47859-8_13
Download citation
DOI: https://doi.org/10.1007/978-3-031-47859-8_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-47858-1
Online ISBN: 978-3-031-47859-8
eBook Packages: Computer ScienceComputer Science (R0)