Skip to main content
Springer Nature Link
Log in

Public-Key Encryption with Quantum Keys

  • Conference paper
  • First Online:
Theory of Cryptography (TCC 2023)

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 14372))

Included in the following conference series:

  • 601 Accesses

Abstract

In the framework of Impagliazzo’s five worlds, a distinction is often made between two worlds, one where public-key encryption exists (Cryptomania), and one in which only one-way functions exist (MiniCrypt). However, the boundaries between these worlds can change when quantum information is taken into account. Recent work has shown that quantum variants of oblivious transfer and multi-party computation, both primitives that are classically in Cryptomania, can be constructed from one-way functions, placing them in the realm of quantum MiniCrypt (the so-called MiniQCrypt). This naturally raises the following question: Is it possible to construct a quantum variant of public-key encryption, which is at the heart of Cryptomania, from one-way functions or potentially weaker assumptions?

In this work, we initiate the formal study of the notion of quantum public-key encryption (qPKE), i.e., public-key encryption where keys are allowed to be quantum states. We propose new definitions of security and several constructions of qPKE based on the existence of one-way functions (OWF), or even weaker assumptions, such as pseudorandom function-like states (PRFS) and pseudorandom function-like states with proof of destruction (PRFSPD). Finally, to give a tight characterization of this primitive, we show that computational assumptions are necessary to build quantum public-key encryption. That is, we give a self-contained proof that no quantum public-key encryption scheme can provide information-theoretic security.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

Notes

  1. 1.

    Throughout this paper, unless explicitly specified, by IND-CCA we refer to the notion of adaptive IND-CCA2 security.

  2. 2.

    Note that PRS implies PRFS with logarithmic size inputs, but no such implication is known for super-logarithmic inputs.

  3. 3.

    Meaning that one can only encrypt once using a .

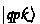  4. 4.

    Because of this stronger security definition, here the notion of public-keys with mixed states is meaningful since there is an alternative procedure to ensure that the key is well-formed (e.g., signing the classical component).

  5. 5.

    This observation was pointed out to us by Takashi Yamakawa.

  6. 6.

    This is due to \(\varPi ^1_\textsf{dk} \) operators being rank-1 projections.

References

  1. Aaronson, S.: Shadow tomography of quantum states. In: Diakonikolas, I., Kempe, D., Henzinger, M. (eds.) 50th ACM STOC, pp. 325–338. ACM Press (2018). https://doi.org/10.1145/3188745.3188802

  2. Alagic, G., Gagliardoni, T., Majenz, C.: Unforgeable quantum encryption. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10822, pp. 489–519. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_16

    Chapter  Google Scholar 

  3. Ananth, P., Gulati, A., Qian, L., Yuen, H.: Pseudorandom (function-like) quantum state generators: New definitions and applications. In: Kiltz, E., Vaikuntanathan, V. (eds.) TCC 2022, Part I. LNCS, vol. 13747, pp. 237–265. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-22318-1_9

  4. Ananth, P., Qian, L., Yuen, H.: Cryptography from pseudorandom quantum states. In: Dodis, Y., Shrimpton, T. (eds.) CRYPTO 2022, Part I. LNCS, vol. 13507, pp. 208–236. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-15802-5_8

  5. Austrin, P., Chung, H., Chung, K.M., Fu, S., Lin, Y.T., Mahmoody, M.: On the impossibility of key agreements from quantum random oracles. In: Dodis, Y., Shrimpton, T. (eds.) CRYPTO 2022, Part II. LNCS, vol. 13508, pp. 165–194. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-15979-4_6

  6. Barhoush, M., Salvail, L.: How to sign quantum messages. arXiv preprint arXiv:2304.06325 (2023)

  7. Barooti, K., et al.: Public-key encryption with quantum keys. Cryptology ePrint Archive, Paper 2023/877 (2023). https://eprint.iacr.org/2023/877

  8. Barooti, K., Malavolta, G., Walter, M.: A simple construction of quantum public-key encryption from quantum-secure one-way functions. Cryptology ePrint Archive, Paper 2023/306 (2023). https://eprint.iacr.org/2023/306

  9. Bartusek, J., Coladangelo, A., Khurana, D., Ma, F.: One-way functions imply secure computation in a quantum world. In: Malkin, T., Peikert, C. (eds.) CRYPTO 2021. LNCS, vol. 12825, pp. 467–496. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84242-0_17

    Chapter  MATH  Google Scholar 

  10. Behera, A., Brakerski, Z., Sattath, O., Shmueli, O.: Pseudorandomness with proof of destruction and applications. Cryptology ePrint Archive, Paper 2023/543 (2023). https://eprint.iacr.org/2023/543

  11. Bennett, C.H., Brassard, G.: An update on quantum cryptography (impromptu talk). In: Blakley, G.R., Chaum, D. (eds.) CRYPTO’84. LNCS, vol. 196, pp. 475–480. Springer, Heidelberg (1984)

    Google Scholar 

  12. Boneh, D., Zhandry, M.: Quantum-secure message authentication codes. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 592–608. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_35

    Chapter  Google Scholar 

  13. Boneh, D., Zhandry, M.: Secure signatures and chosen ciphertext security in a quantum computing world. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 361–379. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_21

    Chapter  MATH  Google Scholar 

  14. Chevalier, C., Ebrahimi, E., Vu, Q.H.: On security notions for encryption in a quantum world. In: Isobe, T., Sarkar, S. (eds.) Progress in Cryptology - INDOCRYPT 2022–23rd International Conference on Cryptology in India, Kolkata, India, 11–14 December 2022, Proceedings. Lecture Notes in Computer Science, vol. 13774, pp. 592–613. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-22912-1_26

  15. Choi, S.G., Dachman-Soled, D., Malkin, T., Wee, H.: A black-box construction of non-malleable encryption from semantically secure encryption. J. Cryptol. 31(1), 172–201 (2018). https://doi.org/10.1007/s00145-017-9254-z

    Article  MathSciNet  MATH  Google Scholar 

  16. Coladangelo, A.: Quantum trapdoor functions from classical one-way functions. Cryptology ePrint Archive, Paper 2023/282 (2023). https://eprint.iacr.org/2023/282

  17. Doliskani, J.: Efficient quantum public-key encryption from learning with errors. Cryptology ePrint Archive, Paper 2020/1557 (2020). https://eprint.iacr.org/2020/1557

  18. Gottesman, D.: Quantum public key cryptography with information-theoretic security (2005). https://www2.perimeterinstitute.ca/personal/dgottesman/Public-key.ppt

  19. Grilo, A.B., Lin, H., Song, F., Vaikuntanathan, V.: Oblivious transfer is in MiniQCrypt. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021. LNCS, vol. 12697, pp. 531–561. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77886-6_18

    Chapter  MATH  Google Scholar 

  20. Grilo, A.B., Sattath, O., Vu, Q.H.: Encryption with quantum public keys. Cryptology ePrint Archive, Paper 2023/345 (2023). https://eprint.iacr.org/2023/345

  21. Huang, H.Y., Kueng, R., Preskill, J.: Predicting many properties of a quantum system from very few measurements. Nat. Phys. 16(10), 1050–1057 (2020)

    Article  Google Scholar 

  22. Impagliazzo, R., Rudich, S.: Limits on the provable consequences of one-way permutations. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 8–26. Springer, New York (1990). https://doi.org/10.1007/0-387-34799-2_2

    Chapter  Google Scholar 

  23. Ji, Z., Liu, Y.-K., Song, F.: Pseudorandom quantum states. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10993, pp. 126–152. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_5

    Chapter  Google Scholar 

  24. Kawachi, A., Koshiba, T., Nishimura, H., Yamakami, T.: Computational indistinguishability between quantum states and its cryptographic application. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 268–284. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_16

    Chapter  Google Scholar 

  25. Kitagawa, F., Morimae, T., Nishimaki, R., Yamakawa, T.: Quantum public-key encryption with tamper-resilient public keys from one-way functions. Cryptology ePrint Archive, Paper 2023/490 (2023). https://eprint.iacr.org/2023/490

  26. Kretschmer, W.: Quantum pseudorandomness and classical complexity. In: Hsieh, M. (ed.) 16th Conference on the Theory of Quantum Computation, Communication and Cryptography, TQC 2021, 5–8 July 2021, Virtual Conference. LIPIcs, vol. 197, pp. 2:1–2:20. Schloss Dagstuhl - Leibniz-Zentrum für Informatik (2021). https://doi.org/10.4230/LIPIcs.TQC.2021.2

  27. Kretschmer, W., Qian, L., Sinha, M., Tal, A.: Quantum cryptography in algorithmica. arXiv preprint arXiv:2212.00879 (2022)

  28. Malavolta, G., Walter, M.: Non-interactive quantum key distribution. Cryptology ePrint Archive, Paper 2023/500 (2023). https://eprint.iacr.org/2023/500

  29. Morimae, T., Yamakawa, T.: One-wayness in quantum cryptography. Cryptology ePrint Archive, Paper 2022/1336 (2022). https://eprint.iacr.org/2022/1336

  30. Morimae, T., Yamakawa, T.: Quantum commitments and signatures without one-way functions. In: Dodis, Y., Shrimpton, T. (eds.) CRYPTO 2022, Part I. LNCS, vol. 13507, pp. 269–295. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-15802-5_10

  31. Myers, S., Shelat, A.: Bit encryption is complete. In: 50th FOCS, pp. 607–616. IEEE Computer Society Press (2009). https://doi.org/10.1109/FOCS.2009.65

  32. Nikolopoulos, G.M., Ioannou, L.M.: Deterministic quantum-public-key encryption: forward search attack and randomization. Phys. Rev. A 79, 042327 (2009). https://doi.org/10.1103/PhysRevA.79.042327

  33. Okamoto, T., Tanaka, K., Uchiyama, S.: Quantum public-key cryptosystems. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 147–165. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44598-6_9

    Chapter  Google Scholar 

  34. Wiesner, S.: Conjugate coding. SIGACT News 15(1), 78–88 (1983). https://doi.org/10.1145/1008908.1008920

    Article  MATH  Google Scholar 

  35. Zhandry, M.: How to construct quantum random functions. In: 53rd FOCS, pp. 679–687. IEEE Computer Society Press (2012). https://doi.org/10.1109/FOCS.2012.37

Download references

Acknowledgments

The authors wish to thank Prabhanjan Ananth and Umesh Vazirani for related discussions, and Takashi Yamakawa for pointing out a simple argument to rule out the existence of information-theoretically secure qPKE. The argument is replicated here with his permission.

ABG and QHV are supported by ANR JCJC TCS-NISQ ANR-22-CE47-0004, and by the PEPR integrated project EPiQ ANR-22-PETQ-0007 part of Plan France 2030. GM was partially funded by the German Federal Ministry of Education and Research (BMBF) in the course of the 6GEM research hub under grant number 16KISK038 and by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy - EXC 2092 CASA - 390781972. OS was supported by the Israeli Science Foundation (ISF) grant No. 682/18 and 2137/19, and by the Cyber Security Research Center at Ben-Gurion University. KB and LH were supported by the Swiss National Science Foundation (SNSF) through the project grant 192364 on Post Quantum Cryptography. OS has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 756482). MW acknowledges support by the the European Union (ERC, SYMOPTIC, 101040907), by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy - EXC 2092 CASA - 390781972, by the BMBF through project QuBRA, and by the Dutch Research Council (NWO grant OCENW.KLEIN.267). Views and opinions expressed are those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them.

Author information

Authors and Affiliations

  1. EPFL, Lausanne, Switzerland

    Khashayar Barooti & Loïs Huguenin-Dumittan

  2. Sorbonne Université, CNRS, LIP6, Paris, France

    Alex B. Grilo & Quoc-Huy Vu

  3. Bocconi University, Milan, Italy

    Giulio Malavolta

  4. Max-Planck Institute in Security and Privacy, Bochum, Germany

    Giulio Malavolta

  5. Computer Science Department, Ben-Gurion University of the Negev, Beersheba, Israel

    Or Sattath

  6. Faculty of Computer Science, Ruhr University Bochum, Bochum, Germany

    Michael Walter

Authors
  1. Khashayar Barooti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alex B. Grilo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Loïs Huguenin-Dumittan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Giulio Malavolta
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Or Sattath
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Quoc-Huy Vu
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Michael Walter
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Quoc-Huy Vu .

Editor information

Editors and Affiliations

  1. Apple, Cupertino, CA, USA

    Guy Rothblum

  2. NTT Research, Sunnyvale, CA, USA

    Hoeteck Wee

Rights and permissions

Reprints and permissions

Copyright information

© 2023 International Association for Cryptologic Research

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Barooti, K. et al. (2023). Public-Key Encryption with Quantum Keys. In: Rothblum, G., Wee, H. (eds) Theory of Cryptography. TCC 2023. Lecture Notes in Computer Science, vol 14372. Springer, Cham. https://doi.org/10.1007/978-3-031-48624-1_8

Download citation

  • DOI: https://doi.org/10.1007/978-3-031-48624-1_8

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-031-48623-4

  • Online ISBN: 978-3-031-48624-1

  • eBook Packages: Computer ScienceComputer Science (R0)

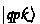Publish with us

Policies and ethics

Societies and partnerships