Abstract
Threshold signatures have emerged as a promising solution to secure cryptocurrencies. While some signature algorithms like Schnorr, BLS, EdDSA are threshold-friendly, the structure of ECDSA makes it challenging to construct such schemes. As such the known threshold ECDSA schemes use complex zero-knowledge proofs. However, these impact their performance negatively. Further, these schemes have attempted to achieve efficiency in signature computation part while accepting complexity in the key generation. To be more specific, in the known 2-of-2 schemes the two parties need to perform key generation together to be able to run signature computation. In this work, we propose an efficient two-party ECDSA protocol that enables two parties to “aggregate” their ECDSA signature (on a single message) without participating in any kind of key generation process. Our protocol is based on additive sharing of (ECDSA) private keys and homomorphic properties of Paillier encryption. All the zero-knowledge proof we use are non-interactive. As a result, our key generation is 7x faster than state-of-the-art. In terms of overall time complexity, our scheme is comparable with state of the art 2-of-2 ECDSA scheme.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Replace key shares with new random ones such that the public key remains the same.
- 2.
Partially Homomorphic Encryption using Alice Paillier keys.
References
Aumasson, J.-P., Hamelink, A., Shlomovits, O.: A survey of ECDSA threshold signing. IACR Cryptol. ePrint Arch. 2020, 1390 (2020)
Aumasson, J.P., Shlomovits, O.: Attacking threshold wallets. Cryptology ePrint Archive, Report 2020/1052 (2020). https://ia.cr/2020/1052
Canetti, R., Gennaro, R., Goldfeder, S., Makriyannis, N., Peled, U.: UC non-interactive, proactive, threshold ECDSA with identifiable aborts. Cryptology ePrint Archive, Paper 2021/060 (2021). https://eprint.iacr.org/2021/060
Castagnos, G., Catalano, D., Laguillaumie, F., Savasta, F., Tucker, I.: Two-party ECDSA from hash proof systems and efficient instantiations. Cryptology ePrint Archive, Paper 2019/503 (2019). https://eprint.iacr.org/2019/503
Castagnos, G., Catalano, D., Laguillaumie, F., Savasta, F., Tucker, I.: Bandwidth-efficient threshold EC-DSA revisited: Online/offline extensions, identifiable aborts, proactivity and adaptive security. Cryptology ePrint Archive, Paper 2021/291 (2021). https://eprint.iacr.org/2021/291
Chainalysis. https://blog.chainalysis.com/reports/2022-crypto-crime-report-introduction/. Accessed 9 Feb 2022
Cramer, R., Damgård, I., Nielsen, J.B.: Multiparty computation from threshold homomorphic encryption. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 280–300. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_18
Damgård, I., Jakobsen, T.P., Nielsen, J.B., Pagter, J.I., Østergaard, M.B.: Fast threshold ECDSA with honest majority. In: Galdi, C., Kolesnikov, V. (eds.) SCN 2020. LNCS, vol. 12238, pp. 382–400. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-57990-6_19
Doerner, J., Kondi, Y., Lee, E., Shelat, A.: Secure two-party threshold ECDSA from ECDSA assumptions. In: 2018 IEEE Symposium on Security and Privacy (SP), pp. 980–997 (2018)
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Gennaro, R., Goldfeder, S.: Fast multiparty threshold ECDSA with fast trustless setup. In: Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security, pp. 1179–1194 (2018)
Gennaro, R., Goldfeder, S.: One round threshold ECDSA with identifiable abort. IACR Cryptol. ePrint Arch. 2020, 540 (2020)
Gennaro, R., Goldfeder, S., Narayanan, A.: Threshold-optimal DSA/ECDSA signatures and an application to bitcoin wallet security. In: Manulis, M., Sadeghi, A.-R., Schneider, S. (eds.) ACNS 2016. LNCS, vol. 9696, pp. 156–174. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-39555-5_9
Goldwasser, S., Micali, S., Rivest, R.L.: A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. 17(2), 281–308 (1988)
Hazay, C., Mikkelsen, G.L., Rabin, T., Toft, T.: Efficient RSA key generation and threshold Paillier in the two-party setting. In: Dunkelman, O. (ed.) CT-RSA 2012. LNCS, vol. 7178, pp. 313–331. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-27954-6_20
Hoffman, P., Wijngaards, W.C.: Elliptic curve digital signature algorithm (DSA) for DNSSEC. RFC 6605, 1–8 (2012)
Itakura, K., Nakamura, K.: A public-key cryptosystem suitable for digital multisignatures. NEC Res. Dev. 71, 1–8 (1983)
Johnson, D., Menezes, A., Vanstone, S.A.: The elliptic curve digital signature algorithm (ECDSA). Int. J. Inf. Sec. 1(1), 36–63 (2001)
Lindell, Y.: Fast secure two-party ECDSA signing. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 613–644. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_21
Lindell, Y., Nof, A.: Fast secure multiparty ECDSA with practical distributed key generation and applications to cryptocurrency custody. In: Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security (2018)
MacKenzie, P., Reiter, M.K.: Two-party generation of DSA signatures. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 137–154. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_8
Wood, G., et al.: Ethereum: a secure decentralised generalised transaction ledger. Ethereum Proj. Yellow Pap. 151(2014), 1–32 (2014)
Xue, H., Au, M.H., Xie, X., Yuen, T.H., Cui, H.: Efficient online-friendly two-party ECDSA signature. In: Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, pp. 558–573 (2021)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
Appendix 1. Elliptic Curve Digital Signature Algorithm
The ECDSA algorithm is parameterized by a group \(\mathcal {G} \) of order q generated by a point \(\texttt{G} \) on an elliptic curve over the finite field \(\mathbb {Z}_q\) of integers modulo a prime q. The curve coordinates and scalars are represented in \(\kappa = |q|\) bits, which is also the security parameter. The algorithm makes use of a hash function which we denote by \(\texttt{HASH} \). The ECDSA scheme consists of the following algorithms:
-
KeyGen: The key generation algorithm consists of the following steps:
-
Select private-key: \(a \xleftarrow {\$} {\mathbb {Z}_q}\)
-
Compute public-key as the point (on \(\mathcal {G} \)) given by \(A = a\cdot \texttt{G} \).
-
-
Sig: The signature generation algorithm takes as input a message \(\texttt{M} \) and computes the signature as below:
-
Hash \(\texttt{M} \) onto \({\mathbb {Z}_q}\): \(m \longleftarrow \texttt{HASH} (\texttt{M})\).
-
Generate nonce: \(k \xleftarrow {\$} {\mathbb {Z}_q}\).
-
Compute \(k \cdot \texttt{G} = R = (x_R, y_R, 1)\) and set \(r = x_R \pmod q\).
-
Set:
 .
. -
Output \(\sigma =(r, \textbf{s})\) as a signature on \(\texttt{M} \)
-
-
Ver: The signature verification algorithm takes as input a message \(\texttt{M} \) and signature \(\sigma =(r,\textbf{s})\) and verifies it as below:
-
Compute
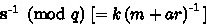
-
Obtain hash of \(\texttt{M} \): \(m \longleftarrow \texttt{HASH} (\texttt{M})\).
-
Set
 (which simplifies to \(k \texttt{G} \))
(which simplifies to \(k \texttt{G} \)) -
If \(x_{R'} = r\) then return ‘signature valid’ else return ‘signature not valid’.
-
Appendix 2. NIZK Proof of Knowledge of Plaintext using Paillier Encryption
We use a NIZK protocol from [7] to prove knowledge of plaintexts \(X_1\) and \(X_2\) in zero knowledge, in Sect. 3.3, under ThreshSig algorithm. The following \(\sum \)-protocol provides a non-interactive ZKP that the prover has knowledge of the plaintext without revealing the plaintext to the approver. Let the input encryption be \(C_1=X_1\cdot G+N\cdot r\mod N^2\), where \(X_1\) is encrypted using randomness r. The proof proceeds as below:
-
1.
Prover P chooses \(x\in \mathbb {Z}_N\), \(u\in \mathbb {Z}_{N^2}^*\) at random and computesthefollowing and sends to the verifier:
$$\begin{aligned} A=x\cdot G +N\cdot u \mod N^2 \end{aligned}$$ -
2.
The verifier picks a random challenge e and sends to the prover P.
-
3.
The prover P computes the following and sends to the verifier:
$$\begin{aligned} w=x+eX_1 \mod N,\ z=u+e\cdot r \mod N^2 \end{aligned}$$ -
4.
The verifier checks the following:
$$\begin{aligned} w\cdot G+N\cdot z {\mathop {=}\limits ^{?}} A+e\cdot C_1\mod N^2 \end{aligned}$$The verifier accepts the proof if and only if the above check passes.
The above \(\sum \) protocol proves knowledge of \(X_1,r\) such that \(C_1=X_1\cdot G+N\cdot r\). A similar protocol is run to prove the knowledge of the plaintext \(X_2\) for ciphertext \(C_2\) with zero knowledge.
Appendix 3. Schnorr’s ZKP for Discrete Log
We give a zero-knowledge proof of discrete logarithm [10] given as input the description of a prime-order group \(\mathbb {G}\) of order q and a generator G, and a group element h. The prover has a witness a value \(x\in \mathbb {Z}_q\) such that \(x\cdot G=h\). The proof of discrete log without revealing the logarithm value proceeds as below:
-
1.
Prover P picks \(r\in \mathbb {Z}_q\), computes the value \(\rho =r\cdot G\) and \(e= \texttt{HASH} (\rho ,G,h)\).
-
2.
Next, it computes \(d=e\cdot x +r \mod q\) and sends \((d,\rho ,h)\) to the verifier.
-
3.
The verifier computes \(f=\texttt{HASH} (\rho , G,h)\) and accepts the proof if and only if the following check is satisfied:
$$\begin{aligned} d\cdot P{\mathop {=}\limits ^{?}} f\cdot h +\rho \end{aligned}$$
The protocol proves the verifier that the prover knows the discrete log of h in zero knowledge.
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Syed, H., Paul, A., Singh, M., Rajan, M. (2023). An Efficient Two-Party ECDSA Scheme for Cryptocurrencies. In: Muthukkumarasamy, V., Sudarsan, S.D., Shyamasundar, R.K. (eds) Information Systems Security. ICISS 2023. Lecture Notes in Computer Science, vol 14424. Springer, Cham. https://doi.org/10.1007/978-3-031-49099-6_25
Download citation
DOI: https://doi.org/10.1007/978-3-031-49099-6_25
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-49098-9
Online ISBN: 978-3-031-49099-6
eBook Packages: Computer ScienceComputer Science (R0)





 .
.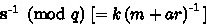
 (which simplifies to
(which simplifies to