Abstract
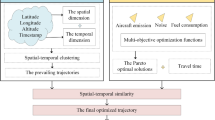
Weather obstacles in the airspace can interfere with an aircraft’s flight plan. Pilots, assisted by air traffic controllers (ATCs), perform avoidance maneuvers that can be optimized. This paper addresses the generation of alternative aircraft trajectories to resolve unexpected events. The authors propose a solution based on the RRG algorithm, K-means clustering, and Dynamic Time Warping (DTW) similarity metric to address the problem. The mixed algorithm succeeds in generating a set of paths with diversity in an obstacle constrained airspace between Paris-Toulouse and London-Toulouse airports. This tool could help to reduce the workload of pilots and ATCs when such a situation arises.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
\(\mu (\mathopen {[}a1,b1\mathclose {]}\times \mathopen {[}a2,b2\mathclose {]})=(b1-a1)*(b2-a2)\) where \(b1>a1\) and \(b2>a2\).
\(\mu (\mathopen {[}a1,b1\mathclose {]}\times \mathopen {[}a2,b2\mathclose {]}\times \mathopen {[}a3,b3\mathclose {]})=(b1-a1)*(b2-a2)*(b3-a3)\) where \(b1>a1\), \(b2>a2\) and \(b3>a3\).
- 2.
In 2D space, \(\zeta _2\) is the surface of a disk of radius 1 (\(\zeta _2=\pi \)).
References
Akgün, V., Erkut, E., Batta, R.: On finding dissimilar paths. Eur. J. Oper. Res. 121(2), 232–246 (2000)
Bellman, R.: On a routing problem. Q. Appl. Math. 16(1), 87–90 (1958)
Bonin, L., Delahaye, D., Guitart, A., Feron, E., Prats, X.: Optimal path planning for soaring flight. In: Conference on Guidance Navigation and control, CEAS EuroGNC 2022, Berlin, Germany, May 2022. CEAS and AIAA (2022). https://hal-enac.archives-ouvertes.fr/hal-03619377
Chakravarty, A.: Four-dimensional fuel-optimal guidance in the presence of winds. J. Guid. Control. Dyn. 8(1), 16–22 (1985)
Chondrogiannis, T., Bouros, P., Gamper, J., Leser, U.: Alternative routing: K-shortest paths with limited overlap. In: Proceedings of the 23rd SIGSPATIAL International Conference on Advances in Geographic Information Systems, SIGSPATIAL 2015, New York, NY, USA. Association for Computing Machinery (2015). https://doi.org/10.1145/2820783.2820858
Cordis and CleanSky: Safency - the safe emergency trajectory generator (2020). https://cordis.europa.eu/project/id/864771/fr
Dijkstra, E.W.: A note on two problems in connexion with graphs. Numer. Math. 1(1), 269–271 (1959). https://doi.org/10.1007/BF01386390
ECMWF: ECMWF datasets (2020). https://www.ecmwf.int/en/forecasts/access-forecasts/access-archive-datasets
Fallast, A., Messnarz, B.: Automated trajectory generation and airport selection for an emergency landing procedure of a CS23 aircraft. CEAS Aeronaut. J. 8(3), 481–492 (2017)
Gierens, K., Matthes, S., Rohs, S.: How well can persistent contrails be predicted? Aerospace 7(12), 169 (2020)
Guitart, A., Delahaye, D., Feron, E.: An accelerated dual fast marching tree applied to emergency geometric trajectory generation. Aerospace 9(4), 180 (2022)
Guitart, A., Delahaye, D., Camino, F.M., Feron, E.: Collaborative generation of local conflict free trajectories with weather hazards avoidance. IEEE Trans. Intell. Transp. Syst. 24, 12831–12842 (2023). https://doi.org/10.1109/TITS.2023.3289191
Hu, X.-B., et al.: Finding the k shortest paths by ripple-spreading algorithms. Eng. Appl. Artif. Intell. 87, 103229 (2020)
Irvine, E.A., Shine, K.P.: Ice supersaturation and the potential for contrail formation in a changing climate. Earth Syst. Dyn. 6(2), 555–568 (2015)
Janson, L., Schmerling, E., Clark, A., Pavone, M.: Fast marching tree: a fast marching sampling-based method for optimal motion planning in many dimensions. arXiv arXiv:1306.3532, February 2015
Jardin, M.R., Bryson, A.E.: Neighboring optimal aircraft guidance in winds. J. Guid. Control. Dyn. 24(4), 710–715 (2001)
Karaman, S., Frazzoli, E.: Incremental sampling-based algorithms for optimal motion planning. arXiv arXiv:1005.0416 (2010)
Karaman, S., Frazzoli, E.: Sampling-based algorithms for optimal motion planning. Int. J. Robot. Res. 30(7), 846–894 (2011)
LaValle, S.M.: Rapidly-exploring random trees : a new tool for path planning. The annual research report (1998)
Lee, D., et al.: The contribution of global aviation to anthropogenic climate forcing for 2000 to 2018. Atmos. Environ. 244, 117834 (2021)
Legrand, K., Puechmorel, S., Delahaye, D., Zhu, Y.: Robust aircraft optimal trajectory in the presence of wind. IEEE Aerosp. Electron. Syst. Mag. 33(11), 30–38 (2018)
Ligny, L., Guitart, A., Delahaye, D., Sridhar, B.: Aircraft emergency trajectory design: a fast marching method on a triangular mesh. In: Fourteenth USA/Europe Air Traffic Management Research and Development Seminar, New-Orleans, United States (2021)
Liu, H., Jin, C., Yang, B., Zhou, A.: Finding top-k shortest paths with diversity. IEEE Trans. Knowl. Data Eng. 30(3), 488–502 (2017)
Palopo, K., Windhorst, R.D., Suharwardy, S., Lee, H.-T.: Wind-optimal routing in the national airspace system. J. Aircr. 47(5), 1584–1592 (2010)
Sáez, R., Khaledian, H., Prats, X.: Generation of emergency trajectories based on aircraft trajectory prediction. In: 2021 IEEE/AIAA 40th Digital Avionics Systems Conference (DASC), pp. 1–10. IEEE (2021)
Sáez, R., Khaledian, H., Prats, X., Guitart, A., Delahaye, D., Feron, E.: A fast and flexible emergency trajectory generator enhancing emergency geometric planning with aircraft dynamics. In: Fourteenth USA/Europe Air Traffic Management Research and Development Seminar, ATM 2021, New Orleans (virtual), United States, September 2021 (2021)
Sethian, J.A.: A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. 93(4), 1591–1595 (1996)
Sethian, J.A., Vladimirsky, A.: Ordered upwind methods for static Hamilton-Jacobi equations. Proc. Natl. Acad. Sci. 98(20), 11069–11074 (2001)
Sáez, R., et al.: An automated emergency airport and off-airport landing site selector. In: 2022 IEEE/AIAA 41st Digital Avionics Systems Conference (DASC), pp. 1–10 (2022). https://doi.org/10.1109/DASC55683.2022.9925757
Soler, M., Zou, B., Hansen, M.: Flight trajectory design in the presence of contrails: application of a multiphase mixed-integer optimal control approach. Transp. Res. Part C Emerg. Technol. 48, 172–194 (2014)
Talarico, L., Sörensen, K., Springael, J.: The k-dissimilar vehicle routing problem. Eur. J. Oper. Res. 244(1), 129–140 (2015)
Yen, J.Y.: Finding the k shortest loopless paths in a network. Manage. Sci. 17(11), 712–716 (1971)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2024 ICST Institute for Computer Sciences, Social Informatics and Telecommunications Engineering
About this paper
Cite this paper
Lebegue, JC., Guitart, A., Demouge, C., Delahaye, D., Hoekstra, J., Feron, E. (2024). Aircraft Cruise Alternative Trajectories Generation: A Mixed RRG-Clustering Approach. In: Martins, A.L., Ferreira, J.C., Kocian, A., Tokkozhina, U., Helgheim, B.I., Bråthen, S. (eds) Intelligent Transport Systems. INTSYS 2023. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, vol 540. Springer, Cham. https://doi.org/10.1007/978-3-031-49379-9_2
Download citation
DOI: https://doi.org/10.1007/978-3-031-49379-9_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-49378-2
Online ISBN: 978-3-031-49379-9
eBook Packages: Computer ScienceComputer Science (R0)