Abstract
The use of pseudorandom function (PRF) and weak PRF as foundational primitives is common in a variety of cryptographic applications, including encryption, authentication, and identification. In this paper, we present a new PRF construction derived from a weak PRF family. Specifically, we propose a derandomization technique from a post-quantum hardness assumption known as learning Burnside homomorphisms with noise (\(B_n\)-LHN). Through the derandomization, a new hardness assumption arises, which we refer to as learning Burnside homomorphisms with rounding (\(B_n\)-LHR). We establish the security of the derandomization by demonstrating that the \(B_n\)-LHR problem is at least as hard as the \(B_n\)-LHN problem.
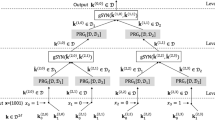
In the work by Naor and Reingold (NR), a PRF construction is introduced based on a weak PRF family, utilizing a novel cryptographic primitive called a pseudorandom synthesizer (PRS). However, this approach necessitates an excessively large key size to design a PRF family. To overcome this issue and produce a more efficient PRF construction, we design a length-doubling pseudorandom generator (PRG) from a weak PRF. Here, the PRG is defined using the secret-key components of a PRF. Notably, in our PRF construction, the length-doubling PRG exhibits efficiency primarily when employed as an intermediate function. We also provide insight into the \(B_n\)-LHR problem by discussing the details of the concatenation operation and error distribution in the Burnside group.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Adian, S.I.: Problema Bernsaida i tozhdestva v gruppakh. Nauka (1975)
Adian, S.I.: The burnside problem and related topics. Russ. Math. Surv. 65(5), 805 (2010)
Ajtai, M.: Generating hard instances of lattice problems extended abstract. In: Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of Computing, pp. 99–108 (1996)
Banerjee, A., Peikert, C., Rosen, A.: Pseudorandom functions and lattices. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 719–737. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_42
Baumslag, G., Fazio, N., Nicolosi, A.R., Shpilrain, V., Skeith, W.E.: Generalized learning problems and applications to non-commutative cryptography. In: Boyen, X., Chen, X. (eds.) ProvSec 2011. LNCS, vol. 6980, pp. 324–339. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24316-5_23
Blum, M., Micali, S.: How to generate cryptographically strong sequences of pseudorandom bits. SIAM J. Comput. 13(4), 850–864 (1984)
Bogdanov, A., Rosen, A.: Pseudorandom functions: three decades later. In: Tutorials on the Foundations of Cryptography. ISC, pp. 79–158. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-57048-8_3
Brakerski, Z., Langlois, A., Peikert, C., Regev, O., Stehlé, D.: Classical hardness of learning with errors. In: Proceedings of the Forty-fifth Annual ACM Symposium on Theory of Computing, pp. 575–584 (2013)
Burnside, W.: On an unsettled question in the theory of discontinuous groups. Quart. J. Pure Appl. Math. 33, 230–238 (1902)
Burnside, W.: The Collected Papers of William Burnside: Commentary on Burnside’s Life and Work; Papers 1883–1899, vol. 1. Oxford University Press (2004)
Fazio, N., Iga, K., Nicolosi, A.R., Perret, L., Skeith, W.E.: Hardness of learning problems over burnside groups of exponent 3. Des. Codes Crypt. 75(1), 59–70 (2015)
Goldreich, O.: A primer on Pseudorandom Generators, vol. 55. American Mathematical Society, Providence (2010)
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM (JACM) 33(4), 792–807 (1986)
Golod, E.S., Shafarevich, I.R.: On the class field tower. Izvestiya Rossiiskoi Akademii Nauk. Seriya Matematicheskaya 28(2), 261–272 (1964)
Gupta, N.: On groups in which every element has finite order. Am. Math. Mon. 96(4), 297–308 (1989)
Hall, M.: Solution of the burnside problem for exponent 6. Proc. Natl. Acad. Sci. U.S.A. 43(8), 751–753 (1957)
Hall, M.: The Theory of Groups. Macmillan Company, New York (1959)
HÅstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999). https://doi.org/10.1137/S0097539793244708
Ivanov, S.V.: The free burnside groups of sufficiently large exponents. Int. J. Algebra Comput. 4, 1–308 (1994)
Joan, D., Vincent, R.: The design of Rijndael: AES-the advanced encryption standard. Information Security and Cryptography (2002)
Katz, J., Lindell, Y.: Introduction to Modern Cryptography. Chapman & Hall/CRC Cryptography and Network Security Series, CRC Press (2020). https://books.google.com/books?id=RsoOEAAAQBAJ
Levi, F., van der Waerden, B.L.: Über eine besondere klasse von gruppen. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 9, 154–158 (1933)
Levin, L.A.: The tale of one-way functions. Probl. Inf. Transm. 39(1), 92–103 (2003)
Luby, M.: Pseudorandomness and Cryptographic Applications, vol. 1. Princeton University Press, Princeton (1996)
Micciancio, D., Regev, O.: Lattice-based cryptography. Post-quantum Cryptography, pp. 147–191 (2009)
Naor, M., Reingold, O.: Synthesizers and their application to the parallel construction of pseudo-random functions. J. Comput. Syst. Sci. 58(2), 336–375 (1999)
Naor, M., Reingold, O.: Number-theoretic constructions of efficient pseudo-random functions. J. ACM (JACM) 51(2), 231–262 (2004)
Regev, O.: New lattice-based cryptographic constructions. J. ACM (JACM) 51(6), 899–942 (2004)
Mihailescu, M.I., Nita, S.L.: Lattice-based cryptography. In: Pro Cryptography and Cryptanalysis, pp. 291–300. Apress, Berkeley, CA (2021). https://doi.org/10.1007/978-1-4842-6367-9_11
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. J. ACM (JACM) 56(6), 1–40 (2009)
Regev, O.: The learning with errors problem. Invited Survey CCC 7(30), 11 (2010)
Regev, O.: The learning with errors problem (invited survey). In: 2010 IEEE 25th Annual Conference on Computational Complexity, pp. 191–204. IEEE (2010)
Robinson, D.J.: A Course in the Theory of Groups, vol. 80. Springer, New York (2012)
Shanov, I.: Solution of the Burnside’s problem for exponent 4. Leningrad State Univ. Ann. (Uchenye Zapiski) Mat. Ser. 10, 166–170 (1940)
Shoup, V.: Sequences of games: a tool for taming complexity in security proofs. cryptology eprint archive (2004)
Shoup, V.: A Computational Introduction to Number Theory and Algebra. Cambridge University Press, New York (2005)
Acknowledgements
We sincerely thank the reviewers for their valuable and insightful feedback on the initial draft of this paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Pandey, D.K., Nicolosi, A.R. (2024). Learning Burnside Homomorphisms with Rounding and Pseudorandom Function. In: Manulis, M., Maimuţ, D., Teşeleanu, G. (eds) Innovative Security Solutions for Information Technology and Communications. SecITC 2023. Lecture Notes in Computer Science, vol 14534. Springer, Cham. https://doi.org/10.1007/978-3-031-52947-4_13
Download citation
DOI: https://doi.org/10.1007/978-3-031-52947-4_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-52946-7
Online ISBN: 978-3-031-52947-4
eBook Packages: Computer ScienceComputer Science (R0)