Skip to main content
Springer Nature Link
Log in

Workforce Allocation for Social Engagement Services via Stochastic Optimization

  • Conference paper
  • First Online:
Recent Advances in Computational Optimization (WCO 2022)

Part of the book series: Studies in Computational Intelligence ((SCI,volume 1158))

Included in the following conference series:

  • 71 Accesses

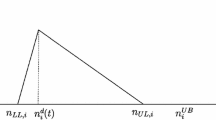
Abstract

Social Engagement is a novel business model whose goal is transforming final users of a service from passive components into active ones. In this framework, people are contacted by the decision-maker (generally a company) and they are asked to perform tasks in exchange for a reward. This paves the way to the interesting optimization problem of allocating the different types of workforce so as to minimize costs. Despite this problem has been investigated within the operations research community, there are no approaches that allow to solve it by explicitly and appropriately modeling the behavior of contacted candidates through consolidated concepts from the utility theory. This work aims at filling this gap, by proposing a stochastic optimization model that includes a chance constraint putting in relation, under probabilistic terms, the candidate willingness to accept a task and the reward actually offered by the decision-maker. The developed model aims at optimally deciding which user to contact, the amount of the reward proposed, and how many employees to use in order to minimize the total expected costs of the operations. An approximation-based solution approach is proposed to address the formulated stochastic optimization problem and its computational efficiency and effectiveness are investigated through an extensive set of computational experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Corno, F., Russis, L.D., Montanaro, T.: Estimate user meaningful places through low-energy mobile sensing. In: 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC). IEEE, October 2016. https://doi.org/10.1109/smc.2016.7844703

  2. Sergi, I., et al.: An IoT-aware smart system to detect thermal comfort in industrial environments. In: 2021 6th International Conference on Smart and Sustainable Technologies (SpliTech). IEEE, September 2021. https://doi.org/10.23919/splitech52315.2021.9566378

  3. Santini, A., Viana, A., Klimentova, X., Pedroso, J.P.: The probabilistic travelling salesman problem with crowdsourcing. Comput. Oper. Res. 142, 105722 (2022). https://doi.org/10.1016/j.cor.2022.105722

    Article  MathSciNet  Google Scholar 

  4. Malagnino, A., Montanaro, T., Lazoi, M., Sergi, I., Corallo, A., Patrono, L.: Building information modeling and internet of things integration for smart and sustainable environments: a review. J. Clean. Prod. 312, 127716 (2021). https://doi.org/10.1016/j.jclepro.2021.127716

    Article  Google Scholar 

  5. Guo, B., Zhang, D., Wang, Z., Yu, Z., Zhou, X.: Opportunistic IoT: exploring the harmonious interaction between human and the internet of things. J. Netw. Comput. App. 36(6), 1531–1539 (2013). https://doi.org/10.1016/j.jnca.2012.12.028

    Article  Google Scholar 

  6. Fadda, E., Perboli, G., Tadei, R.: A progressive hedging method for the optimization of social engagement and opportunistic IoT problems. Eur. J. Oper. Res. 277(2), 643–652 (2019). https://doi.org/10.1016/j.ejor.2019.02.052

    Article  MathSciNet  Google Scholar 

  7. Fadda, E., Perboli, G., Tadei, R.: Customized multi-period stochastic assignment problem for social engagement and opportunistic IoT. Comput. Oper. Res. 93, 41–50 (2018). https://doi.org/10.1016/j.cor.2018.01.010

    Article  MathSciNet  Google Scholar 

  8. Fadda, E., Mana, D., Perboli, G., Tadei, R.: Multi period assignment problem for social engagement and opportunistic IoT. In: 2017 IEEE 41st Annual Computer Software and Applications Conference (COMPSAC). IEEE, July 2017. https://doi.org/10.1109/compsac.2017.173

  9. Alnaggar, A., Gzara, F., Bookbinder, J.H.: Crowdsourced delivery: a review of platforms and academic literature. Omega. 98, 102139 (2021). https://doi.org/10.1016/j.omega.2019.102139

    Article  Google Scholar 

  10. Hanemann, W.M.: Willingness to pay and willingness to accept: how much can they differ? Am. Econ. Rev. 81(3), 635–647 (1991)

    Google Scholar 

  11. Archetti, C., Savelsbergh, M., Speranza, M.G.: The vehicle routing problem with occasional drivers. Eur. J. Oper. Res. 254(2), 472–480 (2016)

    Article  MathSciNet  Google Scholar 

  12. Gdowska, K., Viana, A., Pedroso, J.P.: Stochastic last-mile delivery with crowdshipping. Transp. Res. Proc. 30, 90–100 (2018)

    Google Scholar 

  13. Fishburn, P.C.: Utility theory. Manage. Sci. 14(5), 335–378 (1968)

    Article  Google Scholar 

  14. Paneque, M.P., Bierlaire, M., Gendron, B., Azadeh, S.S.: Integrating advanced discrete choice models in mixed integer linear optimization. Transp. Res. Part B Methodol. 146, 26–49 (2021). https://doi.org/10.1016/j.trb.2021.02.003

    Article  Google Scholar 

  15. Li, P., Arellano-Garcia, H., Wozny, G.: Chance constrained programming approach to process optimization under uncertainty. Comput. Chem. Eng. 32(1–2), 25–45 (2008)

    Article  Google Scholar 

  16. Nemirovski, A., Shapiro, A.: Scenario approximations of chance constraints. In: Probabilistic and Randomized Methods for Design Under Uncertainty, pp. 3–47 (2006)

    Google Scholar 

  17. Margellos, K., Goulart, P., Lygeros, J.: On the road between robust optimization and the scenario approach for chance constrained optimization problems. IEEE Trans. Autom. Control 59(8), 2258–2263 (2014)

    Article  MathSciNet  Google Scholar 

  18. Statistics explained. https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Wages_and_labour_costs

  19. Ermagun, A., Stathopoulos, A.: To bid or not to bid: an empirical study of the supply determinants of crowd-shipping. Transp. Res. Part A Policy Pract. 116, 468–483 (2018). https://doi.org/10.1016/j.tra.2018.06.019

    Article  Google Scholar 

  20. Marcucci, E., Pira, M.L., Carrocci, C.S., Gatta, V., Pieralice, E.: Connected shared mobility for passengers and freight: investigating the potential of crowdshipping in urban areas. In: 2017 5th IEEE International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS). IEEE, June 2017. https://doi.org/10.1109/mtits.2017.8005629

  21. Miller, J., Nie, Y.M., Stathopoulos, A.: Crowdsourced urban package delivery. Transp. Res. Record. J. Transp. Res. Board. 2610(1), 67–75 (2017). https://doi.org/10.3141/2610-08

    Article  Google Scholar 

  22. McFadden, D.: The measurement of urban travel demand. J. Public Econom. 3(4), 303–328 (1974) . https://EconPapers.repec.org/RePEc:eee:pubeco:v:3:y:1974:i:4:p:303-328

  23. Pourrahmani, E., Jaller, M.: Crowdshipping in last mile deliveries: operational challenges and research opportunities. Soc. Econ. Plann. Sci. 78, 101063 (2021). https://doi.org/10.1016/j.seps.2021.101063

    Article  Google Scholar 

  24. Godfrey, V., Powell, W.B.: An adaptive, distribution-free algorithm for the newsvendor problem with censored demands, with applications to inventory and distribution. Manage. Sci. 47(8), 1101–1112 (2001)

    Article  Google Scholar 

  25. Cuzzocrea, A., Fadda, E., Baldo, A.: Lyapunov central limit theorem: theoretical properties and applications in big-data-populated smart city settings. In: 2021 5th International Conference on Cloud and Big Data Computing (ICCBDC). ACM, August 2021. https://doi.org/10.1145/3481646.3481652

Download references

Author information

Authors and Affiliations

  1. Transport and Mobility Laboratory, Ecole Polytechnique Fédérale de Lausanne - CH-1015 EPFL, Lausanne, Switzerland

    Michel Bierlaire

  2. Department of Mathematical Sciences, Politecnico di Torino - corso Duca degli Abruzzi 24, Torino, Italy

    Edoardo Fadda

  3. Department of Control and Computer Engineering, Politecnico di Torino - corso Duca degli Abruzzi 24, Torino, Italy

    Lohic Fotio Tiotsop

  4. Department of Information Engineering, Università degli Studi di Brescia, via Branze 38, Brescia, Italy

    Daniele Manerba

Authors
  1. Michel Bierlaire
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Edoardo Fadda
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lohic Fotio Tiotsop
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Daniele Manerba
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Edoardo Fadda .

Editor information

Editors and Affiliations

  1. Institute of Information and Communication Technologies, Bulgarian Academy of Sciences, Sofia, Bulgaria

    Stefka Fidanova

Rights and permissions

Reprints and permissions

Copyright information

© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Bierlaire, M., Fadda, E., Tiotsop, L.F., Manerba, D. (2024). Workforce Allocation for Social Engagement Services via Stochastic Optimization. In: Fidanova, S. (eds) Recent Advances in Computational Optimization. WCO 2022. Studies in Computational Intelligence, vol 1158. Springer, Cham. https://doi.org/10.1007/978-3-031-57320-0_5

Download citation

Publish with us

Policies and ethics