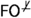Selective Opening Security in the Quantum Random Oracle Model, Revisited

Abstract

We prove that two variants of the Fujisaki-Okamoto transformations are selective opening (SO) secure against chosen-ciphertext attacks in the quantum random oracle model (QROM), assuming that the underlying public-key encryption scheme is one-wayness against chosen-plaintext attacks (OW-CPA). The two variants we consider are (Hofheinz, Hövelmanns, and Kiltz, TCC 2017) and (Jiang et al., CRYPTO 2018). This is the first correct proof in the QROM.

The previous work of Sato and Shikata (IMACC 2019) showed the SO security of in the QROM. However, we identify a subtle gap in their work. To close this gap, we propose a new framework that allows us to adaptively reprogram a QRO with respect to multiple queries that are computationally hard to predict. This is a property that can be easily achieved by the classical ROM, but is very hard to achieve in the QROM. Hence, our framework brings the QROM closer to the classical ROM.

Under our new framework, we construct the first tightly SO secure PKE in the QROM using lossy encryption. Our final application is proving and are bi-selective opening (Bi-SO) secure in the QROM. This is a stronger SO security notion, where an adversary can additionally corrupt some users’ secret keys.

Partially supported by the Research Council of Norway under Project No. 324235.

1 Introduction

Public-key encryption (PKE) schemes are a central topic in cryptography. Their widely accepted security notion is indstinguishability against chosen-ciphertext attacks ($\text {IND}\hbox {-}\text {CCA}$), which states that confidentiality holds even if an adversary $\mathcal {A}$ can adaptively decrypt ciphertexts of its choice, except the challenge ciphertext. This is a security notion in the single-user, single-challenge setting, namely, only one user’s public key and one challenge ciphertext are exposed to an adversary.

Its multi-user, multi-challenge counterpart is an arguably more realistic setting. Selective opening ($\text {SO}$) security [3, 6] is a notion in a multi-challenge setting, where an adversary is given multiple challenge ciphertexts under a single public key and aims at learning some information about the encrypted messages. On top of that, the adversary can open a subset of the challenge ciphertexts and reveal the corresponding messages and randomness used to generate those ciphertexts. $\text {SO}$ security guarantees the confidentiality of the remaining unopened challenge ciphertexts. The recent notion, $\text {Bi}\hbox {-}\text {SO}$ security [28], can be viewed as a stronger variant of the $\text {SO}$ security in a multi-user setting, where the adversary is additionally given multiple users’ public keys and it can corrupt some of their secret keys.

The aforementioned opening capability is motivated by the fact that cryptographic information is technically hard and expensive to erase in practice and an adversary may break into an encrypter’s computer and learn the used randomness. In some applications, such as secure multi-party computation, it is even required to reveal the messages and randomness to make a user’s computation publicly verifiable.

Technically speaking, it is challenging to construct a SO secure PKE. At a first glance, one may think that IND-CCA security implies SO security, since each ciphertext is generated using independent randomness. However, this is not true in general. We refer [23] for an overview and useful further reading. We highlight that, from a provable-security point of view, to answer an opening query, a security reduction should be able to ‘explain’ how it generates a challenge ciphertext by returning the randomness, but in many cases the reduction does not even know the randomness itself. Hybrid arguments are one of the examples, namely, the reduction cannot explain a ciphertext where a challenge is embedded. This is also the inherent reason why the recent updated proof of Sato and Shikata [36] is incorrect. In the recent years, a great amount of effort has been put into defining the right notion of SO security [3, 6, 23] and construct efficient SO-secure public-key encryption schemes [11, 17,18,19,20, 28].

Currently, there are two types of notions have been studied in the literature, the indistinguishability-based (IND-based) ones (weak-IND-SO and full-IND-SO) [3, 6] and the simulation-based (SIM-based) one (SIM-SO) [3]. They are not polynomial-time equivalent to each other. In this paper we only consider the SIM-based one. Informally, SIM-SO security states that for every $\text {SO}$ adversary its output can be efficiently simulated by a simulator that sees only the opened messages. Unlike its IND-based counterpart, SIM-SO does not require the message distribution chosen by the adversary to be efficiently resamplable, conditioned on the opened messages (cf. [3]). Previous work showed that SIM-SO-CCA and full-IND-SO-CCA notions are the strongest SO security [2, 6, 23]. However, only SIM-SO-CCA has been realized so far [11, 17,18,19,20]. It is similar for $\text {Bi}\hbox {-}\text {SO}$ security, and only SIM-based notion is considered so far [28]. For simplicity, we will not write ‘SIM’ in the following.

SO secure PKE schemes are constructed in idealized models [18, 19] and in the standard model [3, 11, 17, 20]. Constructions in idealized models are more efficient and hence more relevant to practice. In particular, this paper considers schemes in the random oracle model (ROM).

The increasing threat that quantum computers can break most widely deployed public-key cryptosystems has driven research in the direction of building post-quantum secure public-key primitives, including PKE schemes and key encapsulation mechanisms (KEMs). Currently, the National Institute of Standards and Technology (NIST) in the US has come to a conclusion for the post-quantum standards. Kyber [37], NTRU [8], and Saber [9] were three finalists in the last round for the KEM/PKE category. They all use variants of the Fujisaki-Okamoto (FO) transformation [12,13,14, 21]. It is interesting to consider whether these FO transformations are secure in the SO setting.

The FO transformation turns a relatively weak PKE (e.g. a One-Way CPA secure one) into an $\text {IND}\hbox {-}\text {CCA}$ secure one. Recently, the FO transformation and its variants have been widely analyzed in both the classical ROM and the quantum (accessible) ROM (QROM) [21, 24, 27, 34, 38], but mostly with a focus on establishing $\text {IND}\hbox {-}\text {CCA}$ security. An exception is the work of Heuer et al. [18] which studied the SO security of the FO transformation in the ROM.

For post-quantum security, proofs in the QROM are more desirable than those in the (classical) ROM, since it models quantum adversaries in a more realistic manner. In this setting, a quantum adversary interacts with a classical network, where “online” primitives (such as encryption) are classical, and computes “offline” primitives (such as hashing) on its own in superposition.

The work of Sato and Shikata [35] proved the SO security of the FO transformation in the QROM. To the best of our knowledge, this is the only work considers SO security in the QROM. However, we identified a subtle gap in their security proof¹. Even worse, this gap cannot be closed, even if we relax the notion to the weaker, non-adaptive SO security as in [29], where an adversary is not allowed to adaptively open a challenge ciphertext, but commits all its opening indices after seeing the challenge ciphertexts. From a technical point of view, closing the gap in [35] requires new proof techniques in the QROM that allow a security reduction to adaptively reprogram multiple RO-queries in one security game without changing the view of an adversary, where the reprogrammed points are computationally hidden. This is a property not achievable by existing well-known techniques, such as [16, 27, 39, 40]. We provide more discussion about it in Sect. 1.2.

1.1 Our Contributions

We revise the selective opening security in the QROM and prove that two “implicit rejection” variants of the FO transformation (namely, [24] and [21]) are $\text {SO}\hbox {-}\text {CCA}$ secure if the underlying PKE is one-way CPA ($\text {OW}\hbox {-}\text {CPA}$) secure in the QROM. Here we consider PKE schemes, namely, combining KEM (or ) with one-time pad and a message authentication code (MAC). The one with is the same scheme considered in [35], but ours is the first correct proof in the QROM. Since the proofs for and are similar, we leave the one for in our full version [33], and there we only prove the $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {CCA}$ for , since it implies $\text {SO}\hbox {-}\text {CCA}$ security.

Our core technical contribution is a computational adaptive reprogramming framework in the QROM that enables a security reduction to adaptively and simultaneously reprogram polynomially many RO-queries which are computationally hidden from a quantum adversary. This is a property that cannot be provided by previous techniques in the QROM, such as the (adaptive) one-way to hiding (O2H) lemma [39, 40], the semi-classical O2H lemma [1], and the measure-rewind-measure O2H lemma [27]. Our framework brings the QROM closer to the classical ROM, and it generalizes and improves the adaptive reprogramming framework by Grilo et al. [16].

Our second contribution is a tightly $\text {SO}\hbox {-}\text {CCA}$ secure PKE from lossy encryption [3, 22]. This is the first tight scheme in the QROM. A recent work of Pan, Wagner, and Zeng has constructed the first tightly multi-user (without corruptions), multi-challenge IND-CCA in the QROM [31], but it did not get extended to the (stronger) SO setting. Another related work is also due to Pan and Zeng [32], where a compact and tightly SO-CCA secure PKE is proposed in the classical random oracle model. However, it is unclear if it can be transformed to the QROM. Our result on tight SO security is established in the QROM, and it improves both aforementioned work.

As another application of our framework, we prove that the aforementioned variants of FO transformation, namely, and , are furthermore $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {CCA}$ secure [28] in the QROM, assuming $\text {OW}\hbox {-}\text {CPA}$ security of the underlying PKE scheme. This notion is stronger than the $\text {SO}\hbox {-}\text {CCA}$ security, since it additionally allows secret key corruption for the adversaries. The only known $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {CCA}$ secure construction is in the classical ROM. Our work is the first one in the QROM.

The NIST finalists Kyber and Saber use tweaked verions of transformation , and NTRU uses . Hence, analysis of these FO transformations is more fundamental than directly analyzing these concrete schemes. Although our results strongly indicate that the NIST finalists are $\text {SO}\hbox {-}\text {CCA}$ secure and $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {CCA}$ in the QROM, we leave the formal proof of it as a future direction, and we are optimistic that our approaches can be extended naturally in achieving it.

1.2 Technical Details

We provide some details about our technical contribution, computational adaptive reprogramming framework.

The work of Heuer et al. [18] is the first one proving that practical PKEs via the OAEP and FO transformation are $\text {SO}\hbox {-}\text {CCA}$ secure in the (classical) ROM. Their work considered the original FO transformation [14]. Motivated by Heuer et al. ’s work, we can show that the combination of and one-time pad is $\text {SO}\hbox {-}\text {CPA}$ secure in the classical ROM by adaptively reprogramming the ROs. Here we describe some key idea. Note that our final goal is $\text {SO}\hbox {-}\text {CCA}$, but for the simplicity of our discussion here, we only consider $\text {SO}\hbox {-}\text {CPA}$.

A ciphertext of message m in the transformation, (e, d), is defined as follow:

(1)

where $\textsf{Enc}_0$ is the randomized encryption algorithm of a $\text {OW}\hbox {-}\text {CPA}$ secure PKE with message space $\mathcal {M}'$, G(r) is the explicit randomness used in $\textsf{Enc}_0$, and G, H are two hash functions with suitable domains and ranges. Public and secret keys of is the same as those of the $\text {OW}\hbox {-}\text {CPA}$ secure PKE, and the decryption is defined in the straightforward way. We refer Fig. 6 for the full description.

To show the $\text {SO}\hbox {-}\text {CPA}$ security, we require “efficient openability” of ciphertexts [3, 11]. This property states that one can generate some ciphertexts and later they can be efficiently opened to arbitrary messages by using some trapdoor (in the standard model) or reprogramming ROs (in the ROM) in a suitable way. In the classical ROM, our ciphertexts (defined by Eq. (1)) have efficient openability. More precisely, a security reduction $\mathcal {R}$ can choose random $r^*_i$, $R^*_i$, and $d^*_i$ and return the challenge ciphertexts $(\textsf{Enc}_0(\textsf{pk},r^*_i;R^*_i), d^*_i)_{1\le i \le \mu }$ to the $\text {SO}\hbox {-}\text {CPA}$ adversary $\mathcal {A}$. For these challenge ciphertexts, the reduction $\mathcal {R}$ can open a ciphertext $(\textsf{Enc}_0(\textsf{pk},r^*_i;R^*_i), d^*_i)$ to arbitrary message $m_i$ by reprogramming $G(r^*_i):=R^*_i$ and $H(r_i^*,e^*_i):=d^*_i \oplus m_i$. Moreover, $\mathcal {R}$ will embed the $\text {OW}\hbox {-}\text {CPA}$ challenge to one of the unopened ciphertexts. Here, $r^*_i$ are only computationally hidden from the adversary.

For the $\text {SO}\hbox {-}\text {CPA}$ security, the aforementioned reprogramming is required to be adaptive, since an adversary can submit an opening query adaptively. Moreover, a $\text {SO}\hbox {-}\text {CPA}$ adversary can submit multiple opening queries in one security game or hybrid. Therefore, our reprogramming strategy should be able to reprogram multiple RO-queries in one security game. We call this last requirement as multi-point reprogramming. We stress that hybrid arguments are already not useful for $\text {SO}$ security. This is because a standard hybrid argument will embed a $\text {OW}\hbox {-}\text {CPA}$ challenge into the $\text {SO}\hbox {-}\text {CPA}$ ciphertexts one-by-one. After it is embedded to the i-th ciphertext, $G(r^*_i)$ cannot be reprogrammed to $R^*_i$, since $R^*_i$ is unknown to the reduction $\mathcal {R}$. Thus, the opening query cannot be correctly answered.

Reprogramming a quantum (accessible) RO is highly non-trivial, since a query in superposition can be viewed as a query that might contain all possible input values at once. To correctly reprogram a value to a particular QRO query, it needs to measure and extract classical preimages of a quantum query, which will cause a change in the adversary’s view. Although many works have been done to provide reprogrammability in the QROM [1, 16, 27, 39, 40], reprogramming in the QROM is still much more challenging than in the ROM.

For the SO security, the situation is more complicated. Essentially, existing approaches (such as [1, 16, 27, 39, 40]) cannot easily achieve the requirements for SO security in the QROM. We use the semi-classical O2H lemma [1] as an example to elaborate on this. Fix a random set $S \subseteq \mathcal {X}$. Let $H,H' : \mathcal {X}\rightarrow \mathcal {Y}$ be two different ROs such that, for all $x\in \mathcal {X}\setminus S$, $H(x)=H'(x)$ (denoted by $H\setminus S = H' \setminus S$). The semi-classical O2H lemma states that a quantum adversary $\mathcal {A}$ cannot tell the difference between H and $H'$ by giving only quantum access to them, unless $\mathcal {A}$ finds an element from S. Here set S needs to be defined before defining H and $H'$.

In the work of Sato and Shikata [35], their security proofs viewed S as the set containing all the randomness used in the opened ciphertexts (cf. the step between Game$_1$ and Game$_2$ in [35, Section 3.1] and the one between Game$_5$ and Game$_6$ in [35, Section 3.2]). Essentially, S is equivalent to the set of opening indices which are adaptively decided by the adversary $\mathcal {A}$. However, to use the semi-classical O2H lemma, S must be fixed at the beginning of the security game, even before generating the public key. Therefore, this technical gap in their proofs cannot be closed, and it will be the case, even if we consider the weaker, non-adaptive variant of SO security as in [29], namely, an adversary cannot adaptively open challenge ciphertexts, but commits to opening indices after receiving the challenge ciphertexts.

The recent measure-rewind-measure O2H lemma [27] has a similar flavor as the semi-classical O2H lemma, and it does not allow to define S adaptively. The adaptive O2H lemma [39] allow us to reprogram a single query adaptively. However, we require adaptive reprogramming multiple queries for SO security, since if we only reprogram wrt one opening query, an adversary can distinguish the simulation by opening multiple ciphertexts.

To solve the technical difficulties, we propose the computational adaptive reprogramming framework. It is more general than the algorithmic O2H lemma [39] and the adaptive reprogramming framework [16] in the sense that our framework allows a reduction to reprogram polynomial many RO queries in the QROM. Different to the work of Grilo et al., our reprogrammed points can be only computationally hidden from the adversary.

In a nutshell, our framework considers two security games, $\textsc {NonAda}$ and $\textsc {Ada}$. The RO $H'$ in $\textsc {NonAda}$ will never be reprogrammed, but the RO H in $\textsc {Ada}$ will be adaptively reprogrammed for multiple times according to the adversary’s behavior. We require $H'\setminus S = H \setminus S$, but S can be modified adaptively by a security reduction. Intuitively, an adversary $\mathcal {A}$ can distinguish $\textsc {NonAda}$ and $\textsc {Ada}$ if it queries $x \in S$. This event can be detected easily in the classical setting, but is problematic in the quantum setting. Our high-level approach is to bound the probability of this event by randomly measuring $\mathcal {A}$. Details are given in Sect. 3. We stress that our approach is not a “hybrid argument” extension of the existing techniques. In fact, as pointed out by Bellare, Hofheinz, and Yilek [3], it is unknown if a simple hybrid argument is useful in proving SO security. Very unfortunately, the latest revision² of [35] is a concrete example for why it does not work. The proof of their Lemma 1 is essentially a hybrid argument. A counterexample is simply: Imagine an adversary that always opens the first ciphertext, then their first hybrid always fails since the OPEN oracle will abort when the adversary opens the first ciphertext, and thus their hybrid argument cannot prove the SO security.

Recently, Grilo et al. proposed the adaptive reprogramming framework [16] and used it to give a QROM proof for Fiat-Shamir’s signatures. The main difference between our work and Grilo et al. ’s work is that their framework requires the reprogramming points to have high statistical entropy, while our framework requires the reprogramming points are computationally hard to find (which cover the case of statistical entropy). When proving the SO security of the FO transformation, their framework cannot be used since the reprogramming points are computationally hidden by OW-CPA security of some underlying PKEs.

We also compare our framework to the measure-and-reprogram framework of Don, Fehr, and Majenz [10] and the lifting theorem in [41] that are used to prove security of the Fiat-Shamir (FS) signature in the QROM. In a nutshell, the difference between our frameworks is similar to that between the security proofs of the FO encryption and FS signature in the classical setting. More precisely, in the proof of FO encryption, we argue that it is infeasible for an adversary to learn the reprogramming points and thus we can reprogram the random oracle without changing the adversary’s view. However, in the proof of FS signature, an adversary can learn the reprogramming points, since they are the hash values of signing messages and some (public) commitments of the $\varSigma$ protocol. Hence, the measure-and-reprogram framework is conceptually different to us and cannot be used in proving SO or Bi-SO security in the QROM. The lifting theorem (cf. [41, Theorem 4.2]) has a similar flavor as the measure-and-reprogram framework.

We leave exploring more applications of our computational adaptive reprogramming framework as a future direction, since reprogramming a (quantum) random oracle on multiple computationally hidden points is an interesting technique and we are optimistic that it may yield new applications. Moreover, we are optimistic that our approach can work for the simulatable DEM framework of SO secure PKEs. We leave a formal treatment of it as another future direction.

2 Preliminaries

Let n be an integer. [n] denotes the set $\{1,...,n\}$. Let ${\mathcal {X}}$ and ${\mathcal {Y}}$ be two finite sets and $f: {\mathcal {X}}\rightarrow {\mathcal {Y}}$ be a function. $f({\mathcal {X}}) := \{f(x) | x \in {\mathcal {X}}\}$. denotes sampling a uniform element x from ${\mathcal {X}}$ at random. If S is a subset of ${\mathcal {X}}$, then ${\mathcal {X}}\backslash S$ denotes the set $\{ x \in {\mathcal {X}}| x \notin S \}$. Let $\mathcal {A}$ be an algorithm. If $\mathcal {A}$ is probabilistic, then $y \leftarrow \mathcal {A}(x)$ means that the variable y is assigned to the output of $\mathcal {A}$ on input x. If $\mathcal {A}$ is deterministic, then we write $y := \mathcal {A}(x)$. We write $\mathcal {A}^{\mathcal {O}}$ to indicate that $\mathcal {A}$ has classical access to oracle $\mathcal {O}$. We write $\textbf{T}(\mathcal {A}_0) \approx \textbf{T}(\mathcal {A}_1)$ if the running times of $\mathcal {A}_0$ and $\mathcal {A}_1$ are polynomially close to each other. All (quantum) algorithms are (quantum) probabilistic polynomial time, unless we state it.

We use code-based games [4] to define and prove security. We implicitly assume that Boolean flags are initialized to false, numerical types are initialized to 0, sets are initialized to $\emptyset$, while strings are initialized to the empty string $\epsilon$. $\Pr [\textbf{G}^\mathcal {A}\Rightarrow 1]$ denotes the probability that the final output $\textbf{G}^{\mathcal {A}}$ of game $\textbf{G}$ running an adversary $\mathcal {A}$ is 1. Let Ev be an (classical and well-defined) event. We write $\Pr [\texttt {Ev} : \textsf {G}]$ to denote the probability that Ev occurs during the game $\textbf{G}$.

We use MAC schemes that have one-time strong existential unforgeability under chosen message attack ($\text {otSUF}\hbox {-}{\text {CMA}}$) as building block. Let $\textsf{MAC}: = (\textsf{Tag}, \textsf{Vrfy})$ be an one-time MAC scheme with key space $\mathcal {K}^\texttt{mac}$. The $\text {otSUF}\hbox {-}{\text {CMA}}$ security game is given in Fig. 1.

Definition 1

(otSUF-CMA). For a forger $\mathcal {F}$, its advantage against $\text {otSUF}\hbox {-}{\text {CMA}}$ security of $\textsf{MAC}$ is defined as

$$\begin{aligned} {\textsf{Adv}}^{\textsf{otSUF}\text{- }\textsf{CMA}}_{\textsf{PKE}}(\mathcal {F}) := \Pr [\textsf{otSUF}\text{- }\textsf{CMA}^{\mathcal {F}}_{\textsf{MAC}} \Rightarrow 1] \end{aligned}$$

$\textsf{MAC}$ is $\text {otSUF}\hbox {-}{\text {CMA}}$ secure if for all $\mathcal {F}$, ${\textsf{Adv}}^{\textsf{otSUF}\text{- }\textsf{CMA}}_{\textsf{PKE}}(\mathcal {F}) = \textsf{negl}(\lambda )$.

One-time MAC schemes can be constructed by using pair-wise independent hash function family, and they are $\text {otSUF}\hbox {-}{\text {CMA}}$ secure against unbounded adversaries. Here $\textsc {Tag}$ cannot be queried with quantum superposition.

Fig. 1.

Security games one-time MAC schemes

2.1 Public-Key Encryption

A Public Key Encryption (PKE) scheme $\textsf{PKE}$ consists of three algorithms $({\textsf{KG}}, \textsf{Enc}, \textsf{Dec})$ and a message space $\mathcal {M}$ that is assumed to be efficiently recognizable. The three algorithms work as follows:

• The key generation algorithm ${\textsf{KG}}$, on input the security parameter $\lambda$, outputs a public and secret key pair $(\textsf{pk},\textsf{sk})$. $\textsf{pk}$ also defines a finite randomness space $\mathcal {R}:= \mathcal {R}(\textsf{pk})$ and a ciphertext space $\mathcal {C}:= \mathcal {C}(\textsf{pk})$. For sake of simplicity, in this paper, we ignore the input $\lambda$ and simply write the process as $(\textsf{pk},\textsf{sk}) \leftarrow {\textsf{KG}}$.

• The encryption algorithm $\textsf{Enc}$, on input $\textsf{pk}$ and a message $m\in \mathcal {M}$, outputs a ciphertext $c \in \mathcal {C}$. We also write $c := \textsf{Enc}(\textsf{pk},m; r)$ to indicate the randomness $r \in \mathcal {R}$ explicitly.

• The (deterministic) decryption algorithm $\textsf{Dec}$, on input $\textsf{sk}$ and a ciphertext c, outputs a message $m' \in \mathcal {M}$ or a rejection symbol $\bot \notin \mathcal {M}$.

Definition 2

(PKE Correctness). A PKE scheme $\textsf{PKE}:= ({\textsf{KG}}, \textsf{Enc}, \textsf{Dec})$ with message space $\mathcal {M}$ is $(1 - \delta )$-correct if

$$ \mathbb {E}\left[ \max _{m \in \mathcal {M}} \Pr \left[ \textsf{Dec}(\textsf{sk},c) \ne m : c \leftarrow \textsf{Enc}(\textsf{pk},m) \right] \right] \le \delta , $$

where the expectation is taken over $(\textsf{pk},\textsf{sk}) \leftarrow {\textsf{KG}}$ and randomness of $\textsf{Enc}$. $\textsf{PKE}$ has perfect correctness if $\delta = 0$.

Definition 3

(Collision Probability of Key Generation). Let

$$\begin{aligned} \eta _{\textsf{PKE}} := \max \left[ \Pr \left[ \textsf{pk}_0 = \textsf{pk}_1 : (\textsf{pk}_0,\textsf{sk}_0) \leftarrow {\textsf{KG}}, (\textsf{pk}_1,\textsf{sk}_1) \leftarrow {\textsf{KG}}\right] \right] \end{aligned}$$

be the collision probability of ${\textsf{KG}}$ of $\textsf{PKE}$. The maximum is taken over all $\textsf{pk}_0,\textsf{pk}_1$. In this paper, we assume that for any $\text {OW}\hbox {-}\text {CPA}$-secure $\textsf{PKE}$, $\eta _{\textsf{PKE}} = \textsf{negl}(\lambda )$

Let $\textsf{PKE}:= ({\textsf{KG}}, \textsf{Enc}, \textsf{Dec})$ be a PKE scheme with message space $\mathcal {M}$ and ciphertext space $\mathcal {C}$. We focus on two security notions for PKE: onewayness under chosen-plaintext attacks ($\text {OW}\hbox {-}\text {CPA}$) and selective-opening security under chosen-ciphertext-attacks ($\text {SO}\hbox {-}\text {CCA}$).

Definition 4

(OW-CPA). For an adversary $\mathcal {A}$, its advantage against $\textsf{OW}\text{- }\textsf{CPA}$ security of $\textsf{PKE}$ is defined as

$\textsf{PKE}$ is $\textsf{OW}\text{- }\textsf{CPA}$ secure if for all PPT adversaries $\mathcal {A}$, ${\textsf{Adv}}^{\textsf{OW}\text{- }\textsf{CPA}}_{\textsf{PKE}}(\mathcal {A}) = \textsf{negl}(\lambda )$.

Selective Opening (SO) security preserves confidentiality even if an adversary opens the randomnesses of some ciphertexts. We use simulation-based approach to define SO security as in [18]. We consider the SO security against Chosen-Plaintext Attacks ($\text {SO}\hbox {-}\text {CPA}$) and Chosen-Ciphertext Attacks ($\text {SO}\hbox {-}\text {CCA}$), respectively.

We note that a non-adaptive variant of SO security has been used in [29], where an adversary must declare the opening index set $I$ after receiving the challenge ciphertexts, while our SO security is adaptive in the sense that $\textsc {Open}$ can be asked adaptively. Intuitively, our adaptive security is harder to achieve, since an adversary can change its opening queries after seeing the answers of previous ones.

Fig. 2.

The SO security games for PKE schemes.

Definition 5

(SO security). Let $\textsf{PKE}$ be a PKE scheme with message space $\mathcal {M}$ and randomness space $\mathcal {R}$ and $\mathcal {A}$ be an adversary against $\textsf{PKE}$. For security parameter $\lambda$, $\mu :=\mu (\lambda )>0$ is a polynomially bounded function. Let ${\textsf{Rel}}$ be a relation. We consider two games defined in Fig. 2, where $\mathcal {A}$ is run in $\textsf{REAL}\hbox {-}\textsf{SO} \hbox {-}\textsf{ATK}_\textsf{PKE}$ and a SO simulator $\mathcal {S}$ in $\textsf{IDEAL}\hbox {-}\textsf{SO} \hbox {-}\textsf{ATK}_\textsf{PKE}$. $\mathcal {M}_a$ is a distribution over $\mathcal {M}$ chosen by $\mathcal {A}$, and $\mathcal {A}$ is not allowed to issue $\textsc {Open}$ queries before it outputs $\mathcal {M}_a$ and receives challenge ciphertexts $\textbf{c}$. Messages sampled from $\mathcal {M}_a$ may be dependent on each other. $\textsc {Dec}$ is not available in $\text {SO}\hbox {-}\text {CPA}$ security.

We define the $\text {SO}\hbox {-}\text {ATK}$ ($\text {ATK}$ = ‘CPA’ or ‘CCA’) advantage function

$$\begin{aligned} {{{\textsf{Adv}}}^{{\textsf{SO}\text{- }\textsf{ATK}}}_{\textsf{PKE}}}&(\mathcal {A},\mathcal {S},\mu , {\textsf{Rel}})\\ &:= \left|\Pr \left[ \textsf{REAL}\hbox {-}\textsf{SO} \hbox {-}\textsf{ATK}_\textsf{PKE}^\mathcal {A}\Rightarrow 1 \right] - \Pr \left[ \textsf{IDEAL}\hbox {-}\textsf{SO} \hbox {-}\textsf{ATK}_\textsf{PKE}^\mathcal {S}\Rightarrow 1 \right] \right|, \end{aligned}$$

$\textsf{PKE}$ is $\text {SO}\hbox {-}\text {ATK}$ secure if, for every adversary $\mathcal {A}$ and every PPT relation $\textsf{Rel}$, there exists a simulator $\mathcal {S}$ such that ${{{\textsf{Adv}}}^{{\textsf{SO}\text{- }\textsf{ATK}}}_{\textsf{PKE}}}(\mathcal {A},\mathcal {S},\mu , {\textsf{Rel}}) \le \textsf{negl}(\lambda )$.

Fig. 3.

The $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {ATK}$ security game for PKE schemes

In this paper, we also consider a stronger SO security definition: $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {ATK}$ [28]. This security definition considers a multi-user setting and allows the adversary to corrupt some users (namely, obtains their secret keys) adaptively. The $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {ATK}$ definition in [28] is non-adaptive, that is, the SO adversary is required to tell the game simulator which users it wants to corrupted and which challenge ciphertexts it wants to open at once. In this paper, we enhance the security definition to be adaptive. The adversary can adaptively issues $\textsc {Open}$ queries and $\textsc {Corrupt}$ queries in any order. The enhanced definition is also simulation-based. If $\mathcal {A}$ corrupts a user $j$, then the messages of challenge ciphertexts that encrypted by $j$ are also revealed (see Items 15 and 16).

Definition 6

(Bi-SO security). Let $\textsf{PKE}$ be a PKE scheme and $\mathcal {A}$ be a Bi-SO adversary against $\textsf{PKE}$. For security parameter $\lambda$, let $\mu :=\mu (\lambda )$ and $p:=p(\lambda )$ that are both polynomially bounded. Let ${\textsf{Rel}}$ be a relation. We consider two games defined in Fig. 3, where $\mathcal {A}$ is run in $\textsf{REAL}\hbox {-}\textsf{Bi} \hbox {-}\textsf{SO} \hbox {-}\textsf{ATK}_{\textsf{PKE}}$ and a Bi-SO simulator $\mathcal {S}$ in $\textsf{IDEAL}\hbox {-}\textsf{Bi} \hbox {-}\textsf{SO} \hbox {-}\textsf{ATK}_{\textsf{PKE}}$. $\mathcal {M}_a$ is a distribution over $\mathcal {M}$ chosen by $\mathcal {A}$, and $\mathcal {A}$ is not allowed to issue $\textsc {Open}$ or $\textsc {Corrupt}$ queries before it outputs $\mathcal {M}_a$ and receives challenge ciphertexts $\textbf{c}$. Messages sampled from $\mathcal {M}_a$ may be dependent on each other. $\textsc {Dec}$ is not available in $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {CPA}$ security.

We define the $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {ATK}$ (ATK = ‘CPA’ or ‘CCA’) advantage function

$$\begin{aligned} &{{\textsf{Adv}}}^{{\textsf{Bi}\hbox {-}\textsf{SO} \hbox {-}\textsf{ATK}}}_{\textsf{PKE}}(\mathcal {A},\mathcal {S},p, \mu , {\textsf{Rel}}) \\ {} & \qquad := \left| \Pr \left[ \textsf{REAL}\hbox {-}\textsf{Bi} \hbox {-}\textsf{SO} \hbox {-}\textsf{ATK}_{\textsf{PKE}}^\mathcal {A}\Rightarrow 1 \right] - \Pr \left[ \textsf{IDEAL}\hbox {-}\textsf{Bi} \hbox {-}\textsf{SO} \hbox {-}\textsf{ATK}_{\textsf{PKE}}^{\mathcal {S}} \Rightarrow 1 \right] \right| . \end{aligned}$$

$\textsf{PKE}$ is adaptive $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {ATK}$ secure if, for any adversary $\mathcal {A}$ and PPT relation $\textsf{Rel}$, there exists a simulator $\mathcal {S}$ such that ${{\textsf{Adv}}}^{{\textsf{Bi}\hbox {-}\textsf{SO} \hbox {-}\textsf{ATK}}}_{\textsf{PKE}}(\mathcal {A},\mathcal {S},p, \mu ,\lambda ) = \textsf{negl}(\lambda )$.

The (Bi-)SO security of PKE schemes containing hash functions can be analyzed in the quantum random oracle model (cf. Sect. 2.2). If we model a hash function H as quantum random oracle, then the adversary $\mathcal {A}$ has quantum access to H during the SO security games (e.g., Fig. 7).

2.2 Quantum Computation

We refer to [30] for detailed background about quantum mechanism. Here we only recall some necessary notations and lemmas.

Pure quantum states can be described by qubits. For a $\lambda$-bit-string x, $|x \rangle \in \mathbb {C}^{2^\lambda }$ denotes the (pure) quantum state of x encoded in the standard computational basis. Quantum register is used to store multiple qubits. In this paper, we assume that any polynomially long object x can be encoded as a (unique) bit string, and if we “store” x in a quantum register X, $|x \rangle$ is the quantum state of this register. A $\lambda$-qubits quantum superposition state $|\phi \rangle$ can be written as $\sum _{x \in \{0,1\}^\lambda } \alpha _x |x \rangle$ where $\sum _{x \in \{0,1\}^\lambda } |\alpha _x|^2 = 1$.

By performing measurement on a quantum state, we obtain classical information about the state, and the state collapses after measurement. Let $|x \rangle$ be an quantum state, $x' \leftarrow \textsf{Measure}(|x \rangle )$ denote the process that $|x \rangle$ is measured and the measurement outcome is $x'$. We assume that all measurement are performed with respect to the standard computational basis.

Let $\mathcal {O}: {\mathcal {X}}\rightarrow {\mathcal {Y}}$ be an random oracle with sets ${\mathcal {X}},{\mathcal {Y}}$. We implicitly assume that the elements in ${\mathcal {X}}$ and ${\mathcal {Y}}$ are expressed as bit strings. In quantum random oracle model (QROM) [7], the oracle $\mathcal {O}$ are described as the unitary transformation $U_{\mathcal {O}}: |x \rangle |y \rangle \rightarrow |x,y \oplus \mathcal {O}(x) \rangle$, and the adversary can query random oracles on quantum states. For an quantum adversary $\mathcal {A}$, the notation $\mathcal {A}^{|\mathcal {O} \rangle }$ indicates that $\mathcal {A}$ has quantum access to the $U_\mathcal {O}$. Without loss of generality, we directly write $\mathcal {O}$ to denote the unitary $U_{\mathcal {O}}$.

In this paper, we say an event is classical if it can be determined by only using classical algorithm (namely, without using any quantum mechanism).

Lemma 1 gives a probabilistic bound for adversary (has a quantum access to oracles) to distinguish $h(s,\cdot )$ and $h'$, where s is secret, h and $h'$ are QRO and have the same image set. When the image is large enough, the adversary cannot distinguish these two oracles.

Lemma 1

(Lemma 2.2 in [34]). Let k be an integer. Let $h: {\mathcal {X}}' \times \mathcal {X} \rightarrow \mathcal {Y}$ and $h': \mathcal {X} \rightarrow \mathcal {Y}$ be two independent random oracles. If an unbounded time quantum adversary $\mathcal {A}$ that queries h at most $q_h$ times, then we have

3 Computational Adaptive Reprogramming in the QROM

We propose a computational adaptive reprogramming framework in the QROM. In our full version [33], we review Unruh’s adaptive O2H lemma [39] and discuss why our lemma (namely, Lemma 2) cannot be proved by using hybrid arguments of Unruh’s adaptive O2H lemma.

Let $\mathcal {A}$ be an adversary that has quantum access to $\mathcal {H}: {\mathcal {X}}\rightarrow {\mathcal {Y}}$ and takes $\textsf{in}_0$ as input and terminates by outputting $\textsf{out}_n$. During its execution, $\mathcal {A}$ outputs some $\textsf{out}_i$ and then takes $\textsf{in}_{i+1}$ as input ($0 \le i \le n-1$). We view $\mathcal {A}$ as a $(n+1)$-stage adversary, $(\mathcal {A}_0,...,\mathcal {A}_n)$, where $\mathcal {A}_i$ takes $\textsf{in}_i$ as input and outputs $\textsf{out}_{i}$. Here $\textsf{in}_0, \textsf{out}_{0}, \textsf{in}_1,..., \textsf{in}_n,$ and $\textsf{out}_n$ can be arbitrary classical information. In this paper, we consider post-quantum setting where adversaries have quantum access to hash functions. The classical information $\textsf{in}_0, \textsf{out}_{0}, \textsf{in}_1,..., \textsf{in}_n, \textsf{out}_n$ capture the interaction between $\mathcal {A}$ and the security game simulator, and they will be specified in a concrete use of our framework.

We write $\mathcal {A}= (\mathcal {A}_0,...,\mathcal {A}_n)$ to divide $\mathcal {A}$ into $n+1$ stages for better analysis. By writing $\textsf{out}_i \leftarrow \mathcal {A}_i(\textsf{in}_i)$ we mean that at stage i $\mathcal {A}$ receives input $\textsf{in}_i$ and outputs $\textsf{out}_i$ at the end of the stage. The index indicates the stage number of $\mathcal {A}$. So, all $\mathcal {A}_i$ are the same adversary $\mathcal {A}$ in different stages, and they share the quantum registers of $\mathcal {A}$. The same notation (of dividing $\mathcal {A}$ into different stages) is also used in Unruh’s adaptive O2H lemma [39].

Games $\textsc {NonAda}$ and $\textsc {Ada}$ (as in Fig. 4) are used to define our framework. $\mathcal {A}$ has quantum access to $\mathcal {H}$ which is either $\textsf{H}$ or $\textsf{H}_i$. In $\textsc {NonAda}$, $\textsf{H}$ will never get reprogrammed, while in $\textsc {Ada}$ different stages of $\mathcal {A}$ will have access to different ROs $\textsf{H}_i$. That is, $\mathcal {A}_i$ queries $\textsf{H}_{i}$, and according to $\mathcal {A}_i$’s output $\textsf{out}_{i}$ $\textsf{H}_{i}$ will be reprogrammed and become $\textsf{H}_{i+1}$ (cf. Items 07, 17 and 18). To formalize this, we define three algorithms $\texttt{INIT}$, $\textsf{F}_\textbf{s}$, and $\textsf{Repro}_\textbf{s}$ in Fig. 4 as:

• $\texttt{INIT}$ outputs $({(\textbf{s},\textsf{in}_0)}, \textsf{H}, \textsf{H}_0)$ (cf. Items 01 and 11), where $\textbf{s}$ is some parameter that used in a security reduction, $\textsf{in}_0$ is the initial input to $\mathcal {A}$, and $\textsf{H}$ and $\textsf{H}_0$ are two random oracles. Here the tuple $({(\textbf{s},\textsf{in}_0)}, \textsf{H}, \textsf{H}_0)$ may have an arbitrary joint distribution.

• $\textsf{F}_\textbf{s}$ takes $\textsf{out}_i$ as input and computes $(\textsf{in}_{i+1}, \textsf{in}'_{i+1})$, where $\textsf{in}_{i+1}$ is the input to $\mathcal {A}_{i+1}$ and $\textsf{in}'_{i+1}$ is the information for reprogramming $\textsf{H}_i$. Here $\textsf{in}'_{i+1}$ is used to capture the fact that $\mathcal {H}$ can be reprogrammed according to $\mathcal {A}_{i}$’s behavior, and the algorithm $\textsf{Repro}_\textbf{s}$ (described below) will take it as input. To make our lemma general and useful for a wider class of applications, we only require that $\textsf{F}_\textbf{s}$ does not have access to random oracles.

• $\textsf{Repro}_\textbf{s}$ is defined to reprogram $\mathcal {H}$ in $\textsc {Ada}$ (cf. Item 17). $\textsf{Repro}_{\textbf{s}}$ takes $\textsf{in}'_{i}$ and $\textsf{H}_{i-1}$ as input. It returns a random oracle $\textsf{H}_{i}$ which is from reprogramming $\textsf{H}_{i-1}$. The concrete reprogramming operation of $\textsf{Repro}_\textbf{s}$ depends on the concrete use of our framework. Here we only require $\textsf{Repro}_\textbf{s}$ to be deterministic.

Fig. 4.

Games $\textsc {NonAda}$ and $\textsc {Ada}$ used in Lemma 2. The main difference between two games is highlighted with gray box. In both games, $\mathcal {A}$ is divided into $n+1$ stages, namely, $(\mathcal {A}_0,...,\mathcal {A}_n)$. The input and output of $\mathcal {A}$ in each stage are classical information because we consider post-quantum settings. The list $\varGamma$ stores $\mathcal {A}$’s outputs in each stage. $\textsf{F}_\textbf{s}$ is a deterministic algorithm that provides inputs for each stage of $\mathcal {A}$. $\textsf{Repro}_\textbf{s}$ is a deterministic algorithm that reprograms QROs. For a concise presentation, we assume that $\mathcal {A}_i$ takes $\mathcal {A}_{i-1}$’s final state as its initial state. In our framework, $\textsf{H}_0$ can be different to $\textsf{H}$.

Let $S_i$ be a set such that $\textsf{H}\setminus S_i = \textsf{H}_i \setminus S_i$ (namely, for all $x \in {\mathcal {X}}$, if $x \in S_i$, then $\textsf{H}(x) \ne \textsf{H}_i(x)$). $\mathcal {A}$ can only distinguish $\textsc {Ada}$ and $\textsc {NonAda}$, if it queries a $x \in S_i$ (where $i \in \{0,...,n\}$). Since $\mathcal {A}$’s QRO queries are superposition states, we need to define extractor $\mathcal {B}_i$ as in Fig. 5 to bound the difference between $\textsc {NonAda}$ and $\textsc {Ada}$. This follows the works in [27, 34, 39]. Lemma 2 formalizes our framework. Its proof is postponed to our full version [33].

Lemma 2

Let $\mathcal {A}$ be an adversary that can be divided into $(n+1)$ stages as in Fig. 4 and has quantum access to random oracle $\mathcal {H}$ ($= \textsf{H}$ in $\textsc {NonAda}$ or $\textsf{H}_i$ in $\textsc {Ada}$). Let $\textsf{Ev}$ be a classical event that may be raised by $\mathcal {A}$ in $\textsc {NonAda}$ or $\textsc {Ada}$. Suppose that $\mathcal {A}$ queries $\mathcal {H}$ at most $q_i$ times in its i-th stage and at most $q:=q_0+\cdots q_n$ times in total during the game. Then for all algorithms $\texttt{INIT}$, $\textsf{F}_{\textbf{s}}$, and $\textsf{Repro}_{\textbf{s}}$ (as described earlier), there exists adversaries $\mathcal {B}_i$ for $i \in \{0,...,n\}$ (shown in Fig. 5) such that

$$\begin{aligned} \Bigl | \Pr \left[ \textsf{Ev}: \textsc {NonAda}^{\mathcal {A}}\right] &- \Pr \left[ \textsf{Ev}: \textsc {Ada}^{\mathcal {A}}\right] \Bigr | \nonumber \\ &\le \sum ^n_{k= 0} \sum ^{k}_{i=0} 2q_i \sqrt{ \Pr \left[ x' \leftarrow \mathcal {B}^\mathcal {H}_i \text { s.t. } x' \in S_i : \textsc {Ada}^{\mathcal {B}_i} \right] } , \end{aligned}$$

(2)

where $S_i$ is a set such that $\textsf{H}\backslash S_i = \textsf{H}_i \backslash S_i$. Such an $S_i$ is defined by the operations in $\textsf{Repro}_\textbf{s}$. $\Pr \left[ \textsf{Ev}: \textsc {NonAda}^{\mathcal {A}}\right]$ and $\Pr \left[ \textsf{Ev}: \textsc {Ada}^{\mathcal {A}}\right]$ are the probabilities that $\mathcal {A}$ triggers $\textsf{Ev}$ in $\textsc {NonAda}$ and in $\textsc {Ada}$, respectively.

In $\textsc {Ada}$, reprogramming the RO is captured by algorithm $\textsf{Repro}_\textbf{s}$. How the reprogramming is done will be specified in a concrete use of Lemma 2. This is to make our framework general. The difference between $\textsc {NonAda}$ and $\textsc {Ada}$ is that between $\textsf{H}$ and $\textsf{H}_i$ caused by $\textsf{Repro}_{\textbf{s}}$.

Fig. 5.

Algorithm $\mathcal {B}_i$ (used in Lemma 2) plays Game $\textsc {Ada}$ (where $i \in [n]$). $\mathcal {B}_i$ proceeds identically with $(\mathcal {A}_1,...,\mathcal {A}_i)$, except that $\mathcal {B}_i$ measures the $t^*$-th QRO query issued by $\mathcal {A}_i$ and then outputs the measurement outcome.

Concretely, in i-th stage, $\textsf{Repro}_\textbf{s}$ will define a set $S_i$ such that $\textsf{H}\setminus S_i = \textsf{H}_i \setminus S_i$. For any $k \in \{0,...,n\}$, if $\mathcal {A}$ queries $\mathcal {H}$ with an $x \in \cup _{0\le i \le k} S_k$ before the end of its k-th stage, then $\mathcal {A}$ can distinguish $\textsc {NonAda}$ and $\textsc {Ada}$. To bound this in the quantum setting, our approach is to randomly measure $\mathcal {A}$’s queries to $\mathcal {H}$, which is captured by $\mathcal {B}_i$ (in Fig. 5). The advantage of $\mathcal {A}$ distinguishing $\textsc {NonAda}$ and $\textsc {Ada}$ is bounded by the probability that $\mathcal {B}_i$’s output falls into $S_i$.

When defining our framework, we do not make any requirement on the efficiencies of $\textsf{F}_{\textbf{s}}$ and $\textsf{Repro}_{\textbf{s}}$. However, when we use this framework to construct (efficient) reduction, $\textsf{F}_{\textbf{s}}$ and $\textsf{Repro}_{\textbf{s}}$ are required to be efficient (namely, running in quantum probabilistic polynomial time) and the description of QRO is polynomially bounded [7, 25, 42]. For instance, we can use a 2q-independent hash function [42] and the list of reprogramming points (which are inputs to the hash and polynomial-bounded) to describe this QRO.

By specifying $\textsf{F}_{\textbf{s}}$ and $\textsf{Repro}_\textbf{s}$, we can describe Grilo et al. ’s framework using our framework (though the bound of our framework is less tight than Grilo et al.’s one). In Grilo et al. ’s framework [16], the i-th output of $\mathcal {A}$ is a distribution $\textsf{out}_i := p_i$. $\textsf{F}_{\textbf{s}}$ can be defined as, on input $p_i$, it samples a reprogramming point $(x_i,x'_i)$ from $p_i$ and an independently random $y_i$ and outputs $(\textsf{in}_{i+1} := (x_i,x'_i), \textsf{in}'_{i+1} := (x_i,x'_i,y_i))$³. $\textsf{Repro}_\textbf{s}$ can be defined as, on input $\textsf{in}'_{i+1} := (x_i,x'_i,y_i)$, it reprograms the QRO $\mathcal {H}:= \mathcal {H}[(x_i, x'_i) \rightarrow y_i]$ and returns the reprogrammed QRO. Their framework implicitly requires that the probability bound for $\mathcal {A}$ to learn $x_i,x'_i$ (before seeing them) is information-theoretic. Namely, $p_i$ should have enough entropy. Some important advantage of our framework, compared with Grilo et al. ’s [16], are as follows:

• Grilo et al. ’s framework requires the reprogramming points have high entropy and it is hard to find them even for unbounded adversary, while our framework does not have such restrictions. If $\mathcal {A}$ is a QPPT adversary, our framework provides efficient extractors $\mathcal {B}_i$’s to bound the difference of $\mathcal {A}$ in $\textsc {NonAda}$ and $\textsc {Ada}$. In our proofs, we need to instantiate $\texttt{INIT}, \textsf{F}_{\textbf{s}}$, and $\textsf{Repro}_{\textbf{s}}$ efficiently. This $\mathcal {B}_i$ can be used to do a reduction in breaking some computational hard problem, for instance, the OW-CPA security. However, the Grilo et al. framework cannot be used to do any efficient reduction.

• Our framework allows $\textsc {NonAda}$ and $\textsc {Ada}$ to start from different QROs, while the Grilo et al. framework starts from the same QRO. Starting from different QROs allows us to consider more complicated cases of adaptive reprogramming. All security proofs in this paper are examples for this, and for SO and Bi-SO security we require this.

• Our framework also supports delayed analysis. In some complicated proofs, the difference between non-reprogramming and reprogramming games cannot be immediately bounded, and we may need extra game sequences to postpone such a bound. Our framework supports delayed analysis, since we can use extra game sequences to bound the winning probability of $\mathcal {B}_i$ (i.e. $\mathcal {B}_i$ outputs $x \in S_i$). In particular, our tightly-secure SO-CCA PKE scheme in Sect. 5 requires delayed analysis.

4 Selective Opening Security of Fujisaki-Okamoto’s PKE in the QROM

We prove the selective-opening ($\text {SO}$) security of two Fujisaki-Okamoto(FO)-style PKE schemes in the QROM. As a warm-up, our first scheme is $\text {SO}$ secure against chosen-plaintext attacks ($\text {SO}\hbox {-}\text {CPA}$), and the scheme follows the idea of hybrid encryption. It offers a simple example about how to use our framework. Our second scheme is $\text {SO}$ secure against chosen-ciphertext attacks ($\text {SO}\hbox {-}\text {CCA}$). It is the same scheme as in [35, Section 3.2], but our proof is showing adaptive $\text {SO}\hbox {-}\text {CCA}$ security, while the original proof in [35] has a subtle gap and the gap still exists even if we consider the non-adaptive security notion (cf. discussion in Introduction).

In both schemes, let $\textsf{PKE}:= ({\textsf{KG}}_0, \textsf{Enc}_0, \textsf{Dec}_0)$ be a $(1 - \delta )$-correct PKE scheme with message space $\mathcal {M}'$, ciphertext space $\mathcal {C}'$, and randomness space $\mathcal {R}'$. Let $G: \mathcal {M}'\rightarrow \mathcal {R}'$ be a hash function.

4.1 Selective Opening Security Against Chosen-Plaintext Attacks

Let $H: \mathcal {M}'\times \mathcal {C}'\rightarrow \mathcal {M}$ be a hash function. Our first PKE scheme $\textsf{wPKE}= (\textsf{wKG}, \textsf{wEnc}, \textsf{wDec})$ (where ‘$\textsf{w}$’ stands for weak) with message space $\mathcal {M}$ and is defined as in Fig. 6. Theorem 1 states that $\textsf{wPKE}$ is adaptive $\text {SO}\hbox {-}\text {CPA}$ secure when modeling G and H as QROs.

Fig. 6.

A $\text {SO}\hbox {-}\text {CPA}$ secure PKE scheme $\textsf{wPKE}= (\textsf{wKG}, \textsf{wEnc}, \textsf{wDec})$

Theorem 1

If $\textsf{PKE}$ is $\text {OW}\hbox {-}\text {CPA}$ secure, then $\textsf{wPKE}$ in Fig. 6 is adaptive $\text {SO}\hbox {-}\text {CPA}$ secure (Definition 5). Concretely, for security parameter $\lambda$ and $\mu := \mu (\lambda )$ (polynomially bounded), for any SO-CPA adversary $\mathcal {A}$ and relation ${\textsf{Rel}}$, there exist a simulator $\mathcal {S}$ and an adversary $\mathcal {B}'$ such that $\textbf{T}(\mathcal {S}) \approx \textbf{T}(\mathcal {A}) \approx \textbf{T}(\mathcal {B}')$ and

$$ {{{\textsf{Adv}}}^{{\textsf{SO}\text{- }\textsf{CPA}}}_{{\textsf{wPKE}}}}(\mathcal {A},\mathcal {S},\mu ,{\textsf{Rel}}) \le 2 (n_{\textsc {O}}+1)^2 q \sqrt{2 \mu {\textsf{Adv}}^{\textsf{OW}\text{- }\textsf{CPA}}_{\textsf{PKE}}(\mathcal {B}')} + \frac{\mu ^2}{|\mathcal {M}|} + \frac{\mu ^2}{|\mathcal {M}'|} + \frac{2\mu q}{\sqrt{|\mathcal {M}'|}}, $$

where $\mu$, $q_G,q_H$, and $n_{\textsc {O}}$ are the maximum numbers of $\mathcal {A}$’s challenge ciphertexts, $\mathcal {A}$’s queries to G, H, and $\textsc {Open}$, respectively. $q = q_G + q_H$.

Proof

Let $h:\mathcal {M}'\times \mathcal {C}'\rightarrow \mathcal {M}$ and $g: \mathcal {M}'\rightarrow \mathcal {R}'$ be two internal quantum-accessible random oracles that are used to respond queries to H and G, respectively. Following the convention in [25, 34], in our proof we simulate H and G using two internal quantum-accessible random oracles $h:\mathcal {M}'\times \mathcal {C}'\rightarrow \mathcal {M}$ and $g: \mathcal {M}'\rightarrow \mathcal {R}'$, respectively.

Fig. 7.

Games $\textbf{G}_{0}^{}$-$\textbf{G}_{3}^{}$ for proving Theorem 1.

Our proof consists a sequence of games defined in Fig. 7. We will use our framework in Sect. 3 to finish the proof. To fit into the syntax of our framework, we combine G and H as one random oracle $G \times H$ such that $G\times H(r',r,e) := (G(r'), H(r,e))$. If $\mathcal {A}$ only queries $G(r')$, we view it as querying $G\times H(r',r,e)$ for some dummy (r, e) and ignoring H(r, e) in the response. $\mathcal {A}$ can query $G\times H$ at most $q = q_H + q_G$ times. This was also used in [24]. $\textbf{G}_{0}^{}$ is equivalent to $\textsf{REAL}\hbox {-}\textsf{SO} \hbox {-}\textsf{CPA}_{\textsf{wPKE}}$, thus

$$ \Pr \left[ {\textsf{REAL}\hbox {-}\textsf{SO} \hbox {-}\textsf{CPA}}^{\mathcal {A}}_{\textsf{wPKE}} \Rightarrow 1 \right] = \Pr \left[ \textbf{G}^{\mathcal {A}}_0 \Rightarrow 1 \right] $$

Game $\textbf{G}_{1}^{}$: If in the challenge ciphertexts there exist $K_i$ and $K_j$ for $i \ne j$ such that $K_i = K_j$, then we abort the game. Such $K_i$ and $K_j$ collide only if $r_i$ and $r_j$ collide or $H(r_i,e_i)$ and $H(r_j,e_j)$ collide with different $r_i$ and $r_j$. By birthday bounds, and we have

$$ \left|\Pr \left[ \textbf{G}^{\mathcal {A}}_0 \Rightarrow 1 \right] - \Pr \left[ \textbf{G}_{1}^{\mathcal {A}} \Rightarrow 1 \right] \right| \le \frac{\mu ^2}{|\mathcal {M}|} + \frac{\mu ^2}{|\mathcal {M}'|} $$

Game $\textbf{G}_{2}^{}$: $R_i$ and $K_i$ in the challenge ciphertexts are chosen randomly, instead of using G and H. If $\mathcal {A}$ queries $\textsc {Open}(i)$, then we reprogram G and H such that $G(r_i) := R_i$ and $H(r_i,e_i) := K_i$.

In the following, we use Lemma 2 to bound the difference between $\textbf{G}_1$ and $\textbf{G}_2$. In $\textbf{G}_2$, $\mathcal {A}$’s $\textsc {Open}$ queries will make QRO $G \times H$ reprogrammed, while in $\textbf{G}_1$, QRO $G \times H$ does not get reprogrammed. So, we can view $\textbf{G}_{1}^{}$ and $\textbf{G}_{2}^{}$ as concrete cases of $\textsc {NonAda}$ and $\textsc {Ada}$, respectively. For simplicity, we denote $\mathcal {A}:= (\mathcal {A}_0, (\mathcal {A}_{1,0},...,\mathcal {A}_{1,n_{\textsc {O}}}))$, where $\mathcal {A}_0$ is the initial stage of $\mathcal {A}$ and cannot query $\textsc {Open}$, and $(\mathcal {A}_{1,0},...,\mathcal {A}_{1,n_{\textsc {O}}})$ is the stage that $\mathcal {A}$ receives the challenge ciphertexts $\textbf{c}$ and can query $\textsc {Open}$. Let $\mathcal {A}_1 := (\mathcal {A}_{1,0},...,\mathcal {A}_{1,n_{\textsc {O}}})$. $\mathcal {A}_1$’s initial state is the final state of $\mathcal {A}_0$. $\mathcal {A}_{1,k}$ is defined with respect to $\textsc {Open}$ queries:

• Before any $\textsc {Open}$ query (i.e., at the 0-th stage), $\mathcal {A}_{1,0}$ takes $\textsf{in}_0:= \textbf{c}$ as input and outputs the first opening index $\textsf{out}_0 := (i_1)$.

• At k-th stage ($1\le k \le n_{\textsc {O}}-1$), $\mathcal {A}_{1,k}$ receives $\textsf{in}_k= (m_{i_k}, r_{i_k})$ As the result of the $(k-1)$-th $\textsc {Open}$ query and finishes the stage by outputting the $(k+1)$-th opening index $\textsf{out}_k := (i_{k+1})$

• Finally, at the $n_{\textsc {O}}$ stage, $\mathcal {A}_{1,n_{\textsc {O}}}$ receives $\textsf{in}_{n_{\textsc {O}}} = (m_{i_{n_{\textsc {O}}}}, r_{i_{n_{\textsc {O}}}})$ and terminates by outputting $\textsf{out}_{n_{\textsc {O}}} = out$ (the final output of SO adversary).

Fig. 8.

Constructions of $\texttt{INIT}, \textsf{F}_{\textbf{s}},$ and $\textsf{Repro}_{\textbf{s}}$ and games $\textbf{G}'_1$ and $\textbf{G}'_2$. $G' := G [r_i\rightarrow R_{i}]$ (similarly, $H' := H [(r_i,e_i) \rightarrow K_i]$) means that we set $G'(r_i):= R_i$ and $G'(r):=G(r)$ for $r\ne r_i$. Oracles $g, g' : \mathcal {M}'\rightarrow \mathcal {R}'$, and $h, h':\mathcal {M}'\times \mathcal {C}'\rightarrow \mathcal {M}$ are four independent internal quantum-accessible random oracles.

To formally show why $\textbf{G}_{1}^{}$ and $\textbf{G}_{2}^{}$ are concrete cases of $\textsc {NonAda}$ and $\textsc {Ada}$, respectively, in Fig. 8, we define $\texttt{INIT}$, $\textsf{F}_{\textbf{s}}$, $\textsf{Repro}_{\textbf{s}}$, $\textbf{G}'_1$ and $\textbf{G}'_2$. Games $\textbf{G}'_1$ and $\textbf{G}'_2$ are only defined to show how our proof follows the syntax of our framework. They have the same forms as $\textsc {NonAda}$ and $\textsc {Ada}$.

Now we argue that $\textbf{G}_{1}^{}$ and $\textbf{G}_{2}^{}$ are concrete cases of $\textsc {NonAda}$ and $\textsc {Ada}$, respectively. Namely, $\textbf{G}_{1}$ and $\textbf{G}_{2}$ in Fig. 7 are equivalent to $\textbf{G}'_{1}$ and $\textbf{G}'_{2}$ in Fig. 8, respectively. Firstly, algorithm $\texttt{INIT}$ in Fig. 8 run the codes from Item 01 to Item 12 in Fig. 7. Since in $\mathcal {A}_0$’s view, $\textbf{G}_1$ is the same as $\textbf{G}_2$ (it does not see any challenge ciphertexts), the distribution of $\mathcal {M}_a$ and $\textbf{m}$ in $\textbf{G}_1$ is the same as the one in $\textbf{G}_2$, and thus the output of $\texttt{INIT}$ and the final state of $\mathcal {A}_0$ in $\texttt{INIT}$ in $\textbf{G}'_{1}$ are the same as those in $\textbf{G}'_2$. Secondly, $\textsf{F}_\textbf{s}$ simulates the $\textsc {Open}$ oracle and $\textsf{Repro}_{\textbf{s}}$ simulates the reprogramming operations on G and H. In $\textbf{G}'_1$, G and H will not be reprogrammed, but in $\textbf{G}'_2$, G and H will be reprogrammed, according to $\mathcal {A}$’s output. This is the same as in $\textbf{G}_2$.

Moreover, when running $\mathcal {A}_{1,k}$, our $\textsf{Repro}_{\textbf{s}}$ defines a set

$$\begin{aligned} S_k := \{(r,(r',e')) \ | \ \exists i\in [\mu ] \backslash I_{k} \text { s.t. } r = r_i\text { or } (r',e') = (r_i,e_i) \} \end{aligned}$$

(3)

where $I_{k} := \{i_1,...,i_{k}\}$ is the opening index set $I$ in $\mathcal {A}_1$’s k-th stage. Answers of $G \times H$ on $S_k$ are only different in $\textbf{G}_{1}^{}$ (i.e., $\textsc {NonAda}$) and $\textbf{G}_{2}^{}$ (i.e., $\textsc {Ada}$). For $k = 0$, $S_0$ is defined at line 35 and $I_0 = \emptyset$.

Now we consider the probability that ${\textsf{Rel}}(\mathcal {M}_a, \textbf{m}, I,out) = 1$. $I$ and $out$ are determined by $\mathcal {A}_1$. $\mathcal {M}_a$ is output by $\mathcal {A}_0$, and $\textbf{m}$ is determined by $\mathcal {M}_a$. Since in $\mathcal {A}_0$’s view, $\textbf{G}_1$ is the same as $\textbf{G}_2$ (since it does not see challenge ciphertexts), thus the distribution of $\mathcal {M}_a$ and $\textbf{m}$ in $\textbf{G}_1$ is the same as the one in $\textbf{G}_2$. Therefore, the probability difference between the classical event that ${\textsf{Rel}}(\mathcal {M}_a, \textbf{m}, I,out) = 1$ in $\textbf{G}_1$ and the similar event in $\textbf{G}_2$, is determined by the probability difference between the event that $\mathcal {A}_1$ outputs a particular $(I,out)$ (i.e., $\varGamma$ in Fig. 8) in $\textbf{G}_1$ and the similar event in $\textbf{G}_2$. Therefore, we have

$$\begin{aligned} &\left| \Pr \left[ \textbf{G}_{1}^{\mathcal {A}} \Rightarrow 1 \right] - \Pr \left[ \textbf{G}_{2}^{\mathcal {A}} \Rightarrow 1 \right] \right| {\le \left| \Pr \left[ \textbf{G}'^{\mathcal {A}_1}_1 \Rightarrow 1 \right] - \Pr \left[ \textbf{G}'^{\mathcal {A}_1}_2 \Rightarrow 1 \right] \right| + \frac{2\mu q}{\sqrt{|\mathcal {M}'|}}} \end{aligned}$$

(4)

This bound includes a term $\frac{2\mu q}{\sqrt{|\mathcal {M}'|}}$, since $\mathcal {A}_0$ also has quantum access to $|G \times H \rangle$, and this term is the probability that the first stage (i.e., $\mathcal {A}_{1,0}$) of $\mathcal {A}_{1}$ learns $r_i$ before seeing challenge ciphertexts. Such probability is only information-theoretic.

We now use Lemma 2 to bound Eq. (4). Since $\textbf{G}'_{1}$ is a $\textsc {NonAda}$ game and $\textbf{G}'_{2}$ is an $\textsc {Ada}$ game, by Lemma 2, there exist adversaries $\mathcal {B}_i$ ($0 \le i \le n_{\textsc {O}}$), which take $\textsf{in}_0 = \textbf{c}$ as its input and output $x \in S_k$ where the set $S_i$ is defined in (3), such that

$$\begin{aligned} \left| \Pr \left[ \textbf{G}'^{\mathcal {A}_1}_1 \Rightarrow 1 \right] - \Pr \left[ \textbf{G}'^{\mathcal {A}_1}_2 \Rightarrow 1 \right] \right| \le \sum _{k=0}^{n_{\textsc {O}}} \sum _{i=0}^k 2 q_i \sqrt{ \Pr \left[ x \leftarrow \mathcal {B}_i \text { s.t. } x \in S_i : \textbf{G}'^{\mathcal {B}_i}_2 \right] } \end{aligned}$$

(5)

Here $\mathcal {B}_i$ proceeds the same as $(\mathcal {A}_{1,0},...,\mathcal {A}_{1,i})$ except that it randomly measures a QRO query issued by $\mathcal {A}_{1,i}$. Moreover, since $\mathcal {A}_{1,0}$’s initial state is the final state of $\mathcal {A}_0$, $\mathcal {B}_i$ starts with state of $\mathcal {A}_0$ (cf. Item 07).

Fig. 9.

The constructions of OW-CPA adversaries $\mathcal {B}'_i$ for $i \in \{0,...,n_{\textsc {O}}\}$. $\mathcal {B}'_i$ simulates $\textbf{G}'_2$ (which is a concrete case of $\textsc {Ada}$ in Fig. 4) for $\mathcal {B}_i$ to break $\textsf{PKE}$. $\textsf{F}$ and $\textsf{Repro}$ are defined as in Fig. 8.

Based on $\mathcal {B}_i$, we construct an adversary $\mathcal {B}'_i$ (in Fig. 9) to break OW-CPA security of $\textsf{PKE}$. By the construction of $\mathcal {B}'_i$, if $\mathcal {A}_1$ does not open $t^*$, and r or $r'$ equals the solution of $e^*$, then $\mathcal {B}'_i$ wins. So the winning probability for $\mathcal {B}'_i$ to break the OW-CPA challenge is:

$$ {\textsf{Adv}}^{\textsf{OW}\text{- }\textsf{CPA}}_{\textsf{PKE}}(\mathcal {B}'_i) = \frac{1}{2} \frac{\mu - n_{\textsc {O}}}{\mu } \frac{1}{\mu - n_{\textsc {O}}} \Pr \left[ x \leftarrow \mathcal {B}_i \text { s.t. } x \in S_i \right] , $$

and thus we have

$$\begin{aligned} \Pr \left[ x \leftarrow \mathcal {B}_i \text { s.t. } x \in S_i : \textbf{G}'^{\mathcal {B}_i}_2 \right] \le 2 \mu {\textsf{Adv}}^{\textsf{OW}\text{- }\textsf{CPA}}_{\textsf{PKE}}(\mathcal {B}'_i) \end{aligned}$$

(6)

Let $\mathcal {B}'$ be the adversary that has highest advantage against $\textsf{PKE}$ among $\{\mathcal {B}'_i\}_{i \in \{0,...,n\}}$. Then Eq. (6) can be written as:

$$\begin{aligned} \Pr \left[ x \leftarrow \mathcal {B}_i \text { s.t. } x \in S_i : \textbf{G}_{2}'^{\mathcal {B}_i} \right] \le 2 \mu {\textsf{Adv}}^{\textsf{OW}\text{- }\textsf{CPA}}_{\textsf{PKE}}(\mathcal {B}'), \text { for } \forall i \in [\mu ] \end{aligned}$$

(7)

By combining Eqs. (4) to (7), we have

$$\begin{aligned} \left| \Pr \left[ \textbf{G}^{\mathcal {A}}_1 \Rightarrow 1 \right] - \Pr \left[ \textbf{G}^{\mathcal {A}}_2 \Rightarrow 1 \right] \right| \le 2 (n_{\textsc {O}}+1)^2 q \sqrt{2 \mu {\textsf{Adv}}^{\textsf{OW}\text{- }\textsf{CPA}}_{\textsf{PKE}}(\mathcal {B}')} + \frac{2\mu q}{\sqrt{|\mathcal {M}'|}} \end{aligned}$$

Game $\textbf{G}_{3}^{}$: We change the generation of $K_i$ and $d_i$. Now we firstly sample $d_i$ uniformly at random, and replace all $K_i$ as $d_i \oplus m_i$. This change is conceptual since in $\textbf{G}_{2}^{}$, all $K_i$ are independently and uniformly random. In $\textbf{G}_{1}^{}$, we excluded any collision of $K_i$, so, in $\textbf{G}_{3}^{}$, it is equivalent to sample $d_i$ in a collision-free way. Therefore, we have

$$\begin{aligned} \Pr \left[ \textbf{G}^{\mathcal {A}}_2 \Rightarrow 1 \right] = \Pr \left[ \textbf{G}^{\mathcal {A}}_3 \Rightarrow 1 \right] \end{aligned}$$

Fig. 10.

The simulator $\mathcal {S}$ of the proof of Theorem 1.

We construct a SO simulator $\mathcal {S}$ that is simulating $\textbf{G}_{3}^{}$ for $\mathcal {A}$ and interacts with the ${\textsf{IDEAL}\hbox {-}\textsf{SO} \hbox {-}\textsf{CPA}}^{\mathcal {S}}_{\textsf{wPKE}}$ game. The simulation process is shown in Fig. 10. Obviously, $\mathcal {S}$ can perfectly simulates $\textbf{G}_{3}^{}$. So, we have

$$ \Pr [\textbf{G}_{3}^{\mathcal {A}} \Rightarrow 1] = \Pr [{\textsf{IDEAL}\hbox {-}\textsf{SO} \hbox {-}\textsf{CPA}}^{\mathcal {S}}_{\textsf{wPKE}} \Rightarrow 1] $$

In conclusion, for any SO-CPA adversary $\mathcal {A}$, there exists efficient simulator $\mathcal {S}$ such that

$$\begin{aligned} &\big |\Pr [{\textsf{REAL}\hbox {-}\textsf{SO} \hbox {-}\textsf{CPA}}^{\mathcal {A}}_{\textsf{wPKE}} \Rightarrow 1] - \Pr [{\textsf{IDEAL}\hbox {-}\textsf{SO} \hbox {-}\textsf{CPA}}^{\mathcal {S}}_{\textsf{wPKE}} \Rightarrow 1] \big | \\ &\qquad \le 2(n_{\textsc {O}}+1)^2 q \sqrt{2 \mu {\textsf{Adv}}^{\textsf{OW}\text{- }\textsf{CPA}}_{\textsf{PKE}}(\mathcal {B}')} + \frac{\mu ^2}{|\mathcal {M}|} + \frac{\mu ^2}{|\mathcal {M}'|} + \frac{2\mu q}{\sqrt{|\mathcal {M}'|}}. \end{aligned}$$

4.2 Selective Opening Security Against Chosen-Ciphertext Attacks

Let $\textsf{MAC}= (\textsf{Tag}, \textsf{Vrfy})$ be a MAC scheme with key space $\mathcal {K}^\texttt{mac}$, and let $H: \mathcal {R}'\times \mathcal {C}'\rightarrow \mathcal {M}\times \mathcal {K}^\texttt{mac}$ be a hash function, where $\mathcal {C}$ is the ciphertext space of $\textsf{PKE}$. The second PKE scheme $\textsf{sPKE}= (\textsf{sKG}, \textsf{sEnc}, \textsf{sDec})$ (Fig. 11) is a combination of a modular Fujisaki-Okamoto’s transformation [21, 24], one-time pad, and the one-time MAC scheme $\textsf{MAC}$. It has similar structure with the scheme in [18, 35].

Fig. 11.

A $\text {SO}\hbox {-}\text {CCA}$ secure PKE scheme $\textsf{sPKE}= (\textsf{sKG},\textsf{sEnc},\textsf{sDec})$

This scheme is adaptive $\text {SO}\hbox {-}\text {CCA}$ secure when modeling G and H as QROs, as stated in Theorem 2. The main difference between the proof of Theorem 2 and the one of Theorem 1 is that the simulator needs to simulate the decryption oracle for the adversary. We use the encrypt-then-hash technique (widely used in CCA proof of PKE [24, 27, 34]) to simulate the decryption oracle without using the secret key and add a MAC verification in the decryption so that the adversary cannot forge valid MAC codes for any unopened cipheretext. We postpone the proof of Theorem 2 to our full version [33].

Theorem 2

If $\textsf{PKE}$ is $\text {OW}\hbox {-}\text {CPA}$ secure and $\delta$-correct, and $\textsf{MAC}$ is $\text {otSUF}\hbox {-}{\text {CMA}}$ secure, then the PKE scheme $\textsf{sPKE}$ in Fig. 11 is adaptive $\text {SO}\hbox {-}\text {CCA}$ secure (Definition 5). Concretely, for security parameter $\lambda$ and integer $\mu := \mu (\lambda )$ (polynomially bounded) for any $\text {SO}\hbox {-}\text {CCA}$ adversary $\mathcal {A}$ and relation ${\textsf{Rel}}$, there exist a simulator $\mathcal {S}$ and adversaries $\mathcal {B}'$ and $\mathcal {F}$ such that $\textbf{T}(\mathcal {S}) \approx \textbf{T}(\mathcal {A}) \approx \textbf{T}(\mathcal {B}') \approx \textbf{T}(\mathcal {F})$ and

$$\begin{aligned} {{{\textsf{Adv}}}^{{\textsf{SO}\text{- }\textsf{CCA}}}_{{\textsf{sPKE}}}}(\mathcal {A},\mathcal {S},\mu ,{\textsf{Rel}}) &\le 6 (n_{\textsc {O}}+1 )^2 q\sqrt{2 \mu {\textsf{Adv}}^{\textsf{OW}\text{- }\textsf{CPA}}_{\textsf{PKE}}(\mathcal {B}') + \mu {\textsf{Adv}}^{\textsf{otSUF}\text{- }\textsf{CMA}}_{\textsf{MAC}}(\mathcal {F}) } \\ &+ 3 \mu {\textsf{Adv}}^{\textsf{otSUF}\text{- }\textsf{CMA}}_{\textsf{MAC}}(\mathcal {F}) + \frac{2 q_H}{\sqrt{2^k}} + 16(\mu + n_{\textsc {D}}+ q + 1)^2 \delta \\ & + \frac{\mu ^2}{|\mathcal {M}|}+ \frac{\mu ^2}{|\mathcal {K}^\texttt{mac}|} + \frac{6\mu q}{\sqrt{|\mathcal {M}'|}} + \frac{\mu n_{\textsc {D}}}{|\mathcal {C}'|- n_{\textsc {D}}} + \frac{(2 + \mu ) q}{\sqrt{|\mathcal {M}'|}} \end{aligned}$$

where $\mu$, $q_G,q_H,n_{\textsc {O}}$, and $n_{\textsc {D}}$ are the maximum numbers of $\mathcal {A}$’s challenge ciphertexts, $\mathcal {A}$’s queries to $G,H,\textsc {Open}$, and $\textsc {Dec}$, respectively. $q = q_G + q_H$.

5 Tight SO-CCA Security from Lossy Encryption

In this section, we show that if the underlying PKE is a lossy encryption [3, 22], then the construction in Fig. 11 is tightly SO-CCA secure. We recall the notion of lossy encryption from [22].

Definition 7

(Lossy Encryption [22]). Let $\textsf{PKE}_1:= (\textsf{KG}_1, \textsf{Enc}_1, \textsf{Dec}_1)$ be a PKE scheme with message space $\mathcal {M}'$ and randomness space $\mathcal {R}'$. $\textsf{PKE}_1$ is lossy if it has the following properties:

• $\textsf{PKE}_1$ is correct according to Definition 2.

• Key indistinguishability: We say $\textsf{PKE}_1$ has key indistinguishability if there is an algorithm $\textsf{LKG}_1$ such that, for any adversary $\mathcal {B}$, the advantage function

  $$ \textsf{Adv}^{\textsf{ind}\hbox {-}\textsf{key}}_{\textsf{PKE}_1}(\mathcal {B}) := | \Pr \left[ \mathcal {B}(\textsf{pk}_1) \Rightarrow 1 \right] - \Pr \left[ \mathcal {B}(\textsf{lpk}_1) \Rightarrow 1 \right] | $$

  is negligible, where $(\textsf{pk}_1,\textsf{sk}_1) \leftarrow \textsf{KG}_1$ and $(\textsf{lpk}_1,\textsf{lsk}_1) \leftarrow \textsf{LKG}_1$.

• Lossiness: Let $(\textsf{lpk}_1,\textsf{lsk}_1) \leftarrow \textsf{LKG}_1$ and $m, m'$ be arbitrary messages in $\mathcal {M}'$, the statistical distance between $\textsf{Enc}_1(\textsf{lpk}_1,m)$ and $\textsf{Enc}_1(\textsf{lpk}_1, m')$ is negligible.

• Weak Openability: Let $(\textsf{lpk}_1,\textsf{lsk}_1) \leftarrow \textsf{KG}_1$, $m$ and $m'$ be arbitrary messages, and $r$ be arbitrary randomness. For ciphertext $c := \textsf{Enc}_1(\textsf{lpk}_1, m; r)$, there exists an algorithm $\textsf{open}_1$ such that $\textsf{open}_1(\textsf{lsk}_1,\textsf{lpk}_1,c,r,m')$ outputs $r'$ where $c = \textsf{Enc}_1(\textsf{lpk}_1, m';r')$ and $r'$ is distributed uniformly. $\textsf{open}_1$ can be inefficient.

The lossiness definition can be extended to a multi-challenge version using a hybrid argument. Since it is only a statistical property, the hybrid argument will not affect tightness of the computational advantage.

Definition 8

(Multi-challenge Lossiness). For any arbitrary messages $m_1, m'_1,...,m_\mu , m'_\mu \in \mathcal {M}'$, the statistical distance between the following distributions D and $D'$ is at most ${\epsilon }^{\textsf{m}\hbox {-}\textsf{ind}\hbox {-}\textsf{enc}}_{\textsf{PKE}_1}$, where ${\epsilon }^{\textsf{m}\hbox {-}\textsf{ind}\hbox {-}\textsf{enc}}_{\textsf{PKE}_1}$ is negligible:

$$\begin{aligned} D &:= \left\{ (\textsf{lpk}_1,c_1,...,c_\mu ) \left| \begin{array}{l} (\textsf{lpk}_1,\textsf{lsk}_1) \leftarrow \textsf{LKG}_1\\ c_1 \leftarrow \textsf{Enc}_1(\textsf{lpk}_1,m_1),...,c_\mu \leftarrow \textsf{Enc}_1(\textsf{lpk}_1,m_\mu ) \end{array}\right. \right\} , \\ D' &:= \left\{ (\textsf{lpk}_1,c'_1,...,c'_\mu ) \left| \begin{array}{l} (\textsf{lpk}_1,\textsf{lsk}_1) \leftarrow \textsf{LKG}_1\\ c'_1 \leftarrow \textsf{Enc}_1(\textsf{lpk}_1,m'_1),...,c'_\mu \leftarrow \textsf{Enc}_1(\textsf{lpk}_1,m'_\mu ) \end{array}\right. \right\} . \end{aligned}$$

5.1 Construction

Let $\textsf{PKE}_1=(\textsf{KG}_1,\textsf{Enc}_1,\textsf{Dec}_1)$ be a lossy encryption with message space $\mathcal {M}'$, randomness space $\mathcal {R}'$, ciphertext space $\mathcal {C}'$, and an opening algorithm $\textsf{open}_1$. Let $\textsf{MAC}= (\textsf{Tag}, \textsf{Vrfy})$ be a MAC scheme with key space $\mathcal {K}^\texttt{mac}$, and $G: \mathcal {M}'\rightarrow \mathcal {R}', H: \mathcal {M}'\times \mathcal {C}'\rightarrow \mathcal {M}\times \mathcal {K}^\texttt{mac}$ be two hash functions. Our PKE scheme $\textsf{sPKE}= (\textsf{sKG}, \textsf{sEnc}, \textsf{sDec})$ is defined in Fig. 12, which has the same structure with the scheme in Fig. 11.

Fig. 12.

A PKE scheme $\textsf{sPKE}= (\textsf{sKG},\textsf{sEnc},\textsf{sDec})$ based on lossy encryption $\textsf{PKE}_1$.

Theorem 3 shows that $\textsf{sPKE}$ is tightly $\text {SO}\hbox {-}\text {CCA}$ secure when modeling G and H as QROs. Although there is a loss $\mu$ to the $\text {otSUF}\hbox {-}{\text {CMA}}$ security of the underlying MAC, if one can use a perfectly $\text {otSUF}\hbox {-}{\text {CMA}}$ secure MAC (e.g., the efficient one implicitly in [26]), it will not affect the security loss of $\textsf{sPKE}$ and thus $\textsf{sPKE}$ is tight.

Theorem 3

If $\textsf{PKE}_1$ is a lossy encryption scheme and $(1-\delta )$-correct, and $\textsf{MAC}$ is $\text {otSUF}\hbox {-}{\text {CMA}}$ secure, then the PKE scheme $\textsf{sPKE}$ in Fig. 12 is adaptive $\text {SO}\hbox {-}\text {CCA}$ secure (Definition 5). Concretely, for security parameter $\lambda$ and integer $\mu := \mu (\lambda )$ (which is polynomially bounded) for any $\text {SO}\hbox {-}\text {CCA}$ adversary $\mathcal {A}$ and relation ${\textsf{Rel}}$, there exist a simulator $\mathcal {S}$ and an adversary $\mathcal {F}$ with $\textbf{T}(\mathcal {S}) \approx \textbf{T}(\mathcal {A})$, $\textbf{T}(\mathcal {F}) \approx \textbf{T}(\mathcal {A})$, and

$$\begin{aligned} {{{\textsf{Adv}}}^{{\textsf{SO}\text{- }\textsf{CCA}}}_{{\textsf{sPKE}}}}&(\mathcal {A},\mathcal {S},\mu ,{\textsf{Rel}}) \\ \le &~ \textsf{Adv}^{\textsf{ind}\hbox {-}\textsf{key}}_{\textsf{PKE}_1}(\mathcal {A}) + 3 \mu {\textsf{Adv}}^{\textsf{otSUF}\text{- }\textsf{CMA}}_{\textsf{MAC}}(\mathcal {F}) \\ &+ 6 (n_{\textsc {O}}+1)^2 q \sqrt{{\epsilon }^{\textsf{m}\hbox {-}\textsf{ind}\hbox {-}\textsf{enc}}_{\textsf{PKE}_1} + \frac{\mu q }{|\mathcal {M}'|}} + 16(\mu + n_{\textsc {D}}+ q + 1)^2 \delta \\ &+ \frac{(2 +\mu ) q}{\sqrt{|\mathcal {M}'|}} + \frac{6 \mu q}{\sqrt{|\mathcal {M}'|}} + \frac{\mu ^2}{|\mathcal {M}'|} + \frac{\mu ^2}{|\mathcal {R}'|} + \frac{\mu ^2}{|\mathcal {K}^\texttt{mac}|} + \frac{\mu n_{\textsc {D}}}{|\mathcal {C}'- n_{\textsc {D}}|} + \frac{\mu ^2}{|\mathcal {M}|} \end{aligned}$$

where $\mu$, $q_G,q_H,n_{\textsc {O}}$, and $n_{\textsc {D}}$ are the maximum numbers of $\mathcal {A}$’s challenge ciphertexts, $\mathcal {A}$’s queries to $G,H,\textsc {Open}$, and $\textsc {Dec}$, respectively. $q = q_G + q_H$.

For simplicity, here we only sketch the proof idea and the formal proof of Theorem 3 is postponed to our full version [33]. Roughly, we firstly use the encrypt-then-hash technique [24, 27, 34] to change security games so that the simulator can simulate decryption oracle without using secret key. Then, we switch the public key of $\textsf{PKE}_1$ to the lossy mode. By the key indistinguishability of $\textsf{PKE}_1$, the adversary cannot detect such modification, and the simulation of decryption oracle still works. However, although the public key is switched to lossy mode, we cannot use the lossiness of $\textsf{PKE}_1$ directly, since there are several correlations between challenge ciphertexts and the QROs. Therefore, at the end of the proof, we use our adaptive reprogramming framework in Sect. 3 and delayed analysis to derelate QROs and challenge ciphertexts, and argue that the adversary cannot learn any information of unopened challenge ciphertexts.

The Regev encryption scheme as defined in [15] is essentially a lossy encryption, and we can use it to instantiate our generic construction in Fig. 12. For completeness, we describe the lossy encryption in our full version [33]. Our resulting LWE-based $\text {SO}\hbox {-}\text {CCA}$ secure PKE is unfortunately only almost tight, since the LWE-based lossy encryption loses a factor depending on the security parameter.

6 Bi-sO Security in the QROM

In this section, we show that two PKE schemes are Bi-sO-CCA secure in the QROM. The first scheme is based on a modular FO transformation [21, 24] (Sect. 6.1). The second scheme is based on another modular FO transformation [21] (Sect. 6.2).

6.1 Bi-sO Security of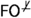 

We show that a multi-user version of $\textsf{sPKE}$ (Fig. 11) is $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {CCA}$-secure in the QROM. Using the same building blocks $\textsf{PKE}= ({\textsf{KG}}_0, \textsf{Enc}_0,\textsf{Dec}_0)$ and $\textsf{MAC}$ as $\textsf{sPKE}$, we propose $\textsf{sPKE}_{\textsf{bi}}$ (in Fig. 13). This scheme can be viewed as a combination of a modular FO transformation in [21, 24], one-time pad, and the a MAC scheme $\textsf{MAC}$. Moreover, in $\textsf{sPKE}_{\textsf{bi}}$, each user includes its public key as an input to the hash functions $G,H,H'$.

Theorem 4 shows that $\textsf{sPKE}_{\textsf{bi}}$ is $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {CCA}$ secure when modeling G and H as QROs. The proof of Theorem 4 is more complicated than the proofs of Theorem 2, since we also need to simulate $\textsc {Corrupt}$ oracle. But the proof idea is similar: we change the games so that the game simulator can use the encrypt-then-hash technique to simulate $\textsc {Dec}$ (as we did in the proof of Theorem 2). To use our framework, we divide $\mathcal {A}_1$ with respect to $\textsc {Corrupt}$ and $\textsc {Dec}$, since the operations of $\textsc {Corrupt}$ also reprograms $G \times H$. The proof of Theorem 4 is postponed to our full version [33].

Fig. 13.

A $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {CCA}$ secure PKE scheme $\textsf{sPKE}_{\textsf{bi}}= (\textsf{sKG},\textsf{sEnc},\textsf{sDec})$

Theorem 4

If $\textsf{PKE}$ is $\text {OW}\hbox {-}\text {CPA}$ secure, then the PKE scheme $\textsf{sPKE}_{\textsf{bi}}$ in Fig. 13 is adaptive $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {CCA}$ secure (Definition 6). Concretely, for any adversary $\mathcal {A}$ and relation ${\textsf{Rel}}$, there exist a simulator $\mathcal {S}$ and adversaries $\mathcal {B}'$ and $\mathcal {F}$ such that $\textbf{T}(\mathcal {S}) \approx \textbf{T}(\mathcal {A}) \approx \textbf{T}(\mathcal {B}') \approx \textbf{T}(\mathcal {F})$ and

$$\begin{aligned} &{{\textsf{Adv}}}^{{\textsf{Bi}\hbox {-}\textsf{SO}\hbox {-}\textsf{CCA}}}_{\textsf{sPKE}_{\textsf{bi}}}(\mathcal {A},\mathcal {S},p, \mu ,{\textsf{Rel}}) \\ {} & \le 6(n_{\textsc {C}}+n_{\textsc {O}}+1)^2 q\sqrt{2 p\mu {\textsf{Adv}}^{\textsf{OW}\text{- }\textsf{CPA}}_{\textsf{PKE}}({\mathcal {B}}^\text {ow}) + p\mu {\textsf{Adv}}^{\textsf{otSUF}\text{- }\textsf{CMA}}_{\textsf{MAC}}(\mathcal {F})} + p\eta _{{\textsf{KG}}_0} \\ &\quad + 3p\mu {\textsf{Adv}}^{\textsf{otSUF}\text{- }\textsf{CMA}}_{\textsf{MAC}}(\mathcal {F}) + \frac{p\mu n_{\textsc {D}}}{|\mathcal {C}'| - n_{\textsc {D}}} + \frac{p^2 \mu ^2 + p^2}{|\mathcal {M}'|} + \frac{p^2 \mu ^2}{|\mathcal {R}'|} + \frac{p^2 \mu ^2}{|\mathcal {M}|} + \frac{p^2 \mu ^2}{|\mathcal {K}^\texttt{mac}|} \\ & \quad + \frac{6p\mu q}{\sqrt{|\mathcal {M}'|}} + 16 p(\mu + n_{\textsc {D}}+ q + q_{H'} + 1)^2 \delta + \frac{2 (n_{\textsc {C}}+1)^2 \sqrt{pq_{H'} } + 2 pq_{H'}+ p\mu q}{\sqrt{|\mathcal {M}'|}} \end{aligned}$$

where $p,\mu$, $q_G,q_H, q_{H'},n_{\textsc {O}},n_{\textsc {C}}$, and $n_{\textsc {D}}$ are the number of user in the games and the maximal numbers of challenge ciphertexts per users, $\mathcal {A}$’s queries to $G,H,H',\textsc {Open}$, $\textsc {Corrupt}$, and $\textsc {Dec}$, respectively. $q = q_G + q_H$.

6.2 Bi-sO Security of 

Let $\textsf{PKE}= ({\textsf{KG}}_0,\textsf{Enc}_0,\textsf{Dec}_0)$ be a deterministic PKE scheme with public space $\mathcal{P}\mathcal{K}'$, plaintext space $\mathcal {M}'$, ciphertext space $\mathcal {C}'$, and plaintext distribution $\mathcal {D}_{\mathcal {M}'}$. Lett $\textsf{MAC}$ be a one-time MAC as in $\textsf{sPKE}_{\textsf{bi}}$. Let $H: \mathcal{P}\mathcal{K}'\times \mathcal {M}'\rightarrow \mathcal {M}\times \mathcal {K}^\texttt{mac}$ and $H': \mathcal{P}\mathcal{K}'\times \mathcal {M}'\times \mathcal {C}'\rightarrow \mathcal {M}\times \mathcal {K}^\texttt{mac}$ be two hash functions. We define $\textsf{sPKE}^\textsf{m}_{\textsf{bi}}$ as in Fig. 14. $\textsf{sPKE}^\textsf{m}_{\textsf{bi}}$ can be viewed as a combination of [21], one-time pad and one-time MAC. Similar to $\textsf{sPKE}_{\textsf{bi}}$, each user includes its public key into the input of hash functions.

Fig. 14.

A ${\textsf{Bi}\hbox {-}\textsf{SO}\hbox {-}\textsf{CCA}}$ secure PKE scheme $\textsf{sPKE}^\textsf{m}_{\textsf{bi}}= (\textsf{sKG}^\textsf{m}_{\textsf{bi}},\textsf{sEnc}^\textsf{m}_{\textsf{bi}},\textsf{sDec}^\textsf{m}_{\textsf{bi}})$

Here we consider a variant of OW-CPA security: $\mathcal {D}_{\mathcal {M}'}$-$\textsf{OW}\text{- }\textsf{CPA}$ security, namely, $\textsf{OW}\text{- }\textsf{CPA}$ security with challenge messages chosen following $\mathcal {D}_{\mathcal {M}'}$. For simplicity, the definition of of $\mathcal {D}_{\mathcal {M}'}$-$\textsf{OW}\text{- }\textsf{CPA}$ is given in our full version [33]. Moreover, we require that $\textsf{PKE}$ is rigid correct [5], namely, for all $(\textsf{pk},\textsf{sk})$ generated from ${\textsf{KG}}_0$, ciphertext e, and plaintext r, $(e = \textsf{Enc}_0(\textsf{pk},r))$ if and only if $(\textsf{Dec}_0(\textsf{sk},e) = r)$. Theorem 5 shows that $\textsf{sPKE}^\textsf{m}_{\textsf{bi}}$ is Bi-sO-CCA secure when modeling G, H,  and $H'$ as QROs. The proof of Theorem 5 is similar to Theorem 4, and is postponed to our full version [33].

Theorem 5

Let $\textsf{PKE}$ be a deterministic PKE with perfect correctness and rigidity. If $\textsf{PKE}$ is $\mathcal {D}_{\mathcal {M}'}$-$\text {OW}\hbox {-}\text {CPA}$ secure, then the PKE scheme $\textsf{sPKE}^\textsf{m}_{\textsf{bi}}$ in Fig. 14 is adaptive $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {CCA}$ secure (Definition 6). Concretely, for any $\text {Bi}\hbox {-}\text {SO}\hbox {-}\text {CCA}$ adversary $\mathcal {A}$ and relation ${\textsf{Rel}}$, there exist a simulator $\mathcal {S}$ and adversaries $\mathcal {B}^\text {ow}$ and $\mathcal {F}$ such that $\textbf{T}(\mathcal {S}) \approx \textbf{T}(\mathcal {A}) \approx \textbf{T}(\mathcal {B}') \approx \textbf{T}(\mathcal {F})$ and

$$\begin{aligned} &{{\textsf{Adv}}}^{{\textsf{Bi}\hbox {-}\textsf{SO}\hbox {-}\textsf{CCA}}}_{\textsf{sPKE}_{\textsf{bi}}}(\mathcal {A},\mathcal {S},p, \mu ,{\textsf{Rel}})\\ &\le 6(n_{\textsc {C}}+n_{\textsc {O}}+1)^2 q\sqrt{2 p\mu {\textsf{Adv}}^{\textsf{OW}\text{- }\textsf{CPA}}_{\textsf{PKE}, \mathcal {D}_{\mathcal {M}'}}({\mathcal {B}}^\text {ow}) + p\mu {\textsf{Adv}}^{\textsf{otSUF}\text{- }\textsf{CMA}}_{\textsf{MAC}}(\mathcal {F})} \\ & \quad + 3p\mu {\textsf{Adv}}^{\textsf{otSUF}\text{- }\textsf{CMA}}_{\textsf{MAC}}(\mathcal {F}) + \frac{6p\mu q}{2^{\epsilon _{\mathcal {D}_{\mathcal {M}'}}}} + \frac{p\mu n_{\textsc {D}}}{|\mathcal {C}'| - n_{\textsc {D}}} + \frac{p^2 \mu ^2 + p^2}{|\mathcal {M}'|} + \frac{p^2 \mu ^2}{|\mathcal {M}|} \\ & \quad + p\eta _{{\textsf{KG}}_0} + \frac{p^2 \mu ^2}{|\mathcal {K}^\texttt{mac}|} + \frac{2 (n_{\textsc {C}}+1)^2 \sqrt{pq_{H'} } + 2 pq_{H'}+ p\mu q}{\sqrt{|\mathcal {M}'|}} \end{aligned}$$

where $p,\mu$, $q_H, q_{H'},n_{\textsc {O}},n_{\textsc {C}}$, and $n_{\textsc {D}}$ are the maximum numbers of user in the games and $\mathcal {A}$’s challenge ciphertexts per users, $\mathcal {A}$’s queries to $H,H',\textsc {Open}$, $\textsc {Corrupt}$, and $\textsc {Dec}$, respectively. $\epsilon _{\mathcal {D}_{\mathcal {M}'}}$ is the minimum entropy of $\mathcal {D}_{\mathcal {M}'}$.

Appendices

Supporting Material

A Review of Adaptive One-Way-to-Hiding

Let $\mathcal{H}\mathcal{F}:= \{\{0,1\}^* \rightarrow \{0,1\}^n \}$ be a set containing all functions that have $\{0,1\}^*$ as domain and $\{0,1\}^n$ as codomain. Let $\mathcal {A}= (\mathcal {A}_0, \mathcal {A}_1)$ be an adversary that has quantum access to a QRO $\mathcal {H}$ and queries it at most $q_0+q_1$ times. Unruh’s adaptive OW2H lemma [39, Lemma 15] can be described as follows: let

where $q_0$, $q_1$ are the numbers of time $\mathcal {A}_0,\mathcal {A}_1$ queries $\mathcal {H}$ respectively. C is an algorithm that has quantum access to $\mathcal {H}$ and on input (j, B, x), runs $\mathcal {A}^{\mathcal {H}}_1(x,B)$ until its j-th query, measures the QRO query in the computational basis, output the measurement outcome. Then

$$\begin{aligned} \left| P^\mathcal {A}_0 - P^\mathcal {A}_1 \right| \le 2q_1 \sqrt{P_C} + q_0 2^{-l/2 + 2} \end{aligned}$$

The bound given in this adaptive OW2H lemma includes two parts: the first part is roughly the search bound of quantum adversaries to find a uniformly random x given $\mathcal {H}(x||m)$ (i.e., $q_0 2^{-l/2 + 2}$), and the second part is the advantage of $\mathcal {A}_1$ to distinguish two QROs: $\mathcal {H}_{(x||m)\rightarrow B}$ and $\mathcal {H}$, where $\mathcal {H}_{(x||m)\rightarrow B}$ is the same as $\mathcal {H}$ except that $\mathcal {H}_{(x||m)\rightarrow B}(x||m) = B$. Note that this advantage is described by the extracting algorithm C.

Unruh’s adaptive OW2H lemma cannot be used to prove the bound of our reprogramming framework Fig. 4 via hybrid arguments. This is because:

• The initial oracles of $\textsc {Ada}$ and $\textsc {NonAda}$ in our framework are not necessarily the same. In this case, our framework considers a stronger QROM adaptive reprogramming setting than the adaptive OW2H (and the adaptive reprogramming framework in [16]).

• Even if the initial oracles are the same, in our framework, sets $S_i$ may not independent to each other, and thus each intermediate hybrid games in the hybrid argument may not independent. This makes it hard to modify the adaptive OW2H lemma to fit in our framework and use hybrid argument. More details will be given in our full version [33].