Abstract
Traditional private set intersection (PSI) involves a receiver and a sender holding sets X and Y, respectively, with the receiver learning only the intersection \(X\cap Y\). We turn our attention to its fuzzy variant, where the receiver holds \(|X|\) hyperballs of radius \(\delta \) in a metric space and the sender has |Y| points. Representing the hyperballs by their center, the receiver learns the points \(x\in X\) for which there exists \(y\in Y\) such that \(\textsf{dist}(x,y)\le \delta \) with respect to some distance metric. Previous approaches either require general-purpose multi-party computation (MPC) techniques like garbled circuits or fully homomorphic encryption (FHE), leak details about the sender’s precise inputs, support limited distance metrics, or scale poorly with the hyperballs’ volume.
This work presents the first black-box construction for fuzzy PSI (including other variants such as PSI cardinality, labeled PSI, and circuit PSI), which can handle polynomially large radius and dimension (i.e., a potentially exponentially large volume) in two interaction messages, supporting general \(L_{\textsf{p}\in [1,\infty ]}\) distance, without relying on garbled circuits or FHE. The protocol excels in both asymptotic and concrete efficiency compared to existing works. For security, we solely rely on the assumption that the Decisional Diffie-Hellman (DDH) holds in the random oracle model.
A. van Baarsen—Research partially funded by NWO/TKI Grant 628.009.014.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Private set intersection (PSI) is a cryptographic primitive that allows two parties to compute the intersection \(X\cap Y\) of their private datasets X and Y, without revealing any information about items not in the intersection. The first PSI protocol is often dated back to Meadows [30] and many modern protocols still have the same structure using an oblivious pseudorandom function (OPRF) [28, 35, 36]. Recent PSI protocols are very practical and can for example compute the intersection of sets of \(2^{20}\) elements in \({\approx }{0.37}\) s [35]. Many richer PSI functionalities have also been explored, such as: PSI cardinality [16, 18, 27], where only the cardinality of the intersection is revealed; labeled PSI [10, 13, 14], which allows the parties to learn labels associated to the items in the intersection; circuit PSI [24, 34, 36], which only reveals secret shares of the intersection and allows the parties to securely evaluate any function on the intersection.
Recently Garimella et al. [20, 21] introduced the concept of structure-aware PSI, where the receiver’s input set has some publicly known structure. For example, the receiver holds N balls of radius \(\delta \) and dimension d and the sender holds a set of M points, and the sender learns which of the sender’s points lie within one of their balls. This special case is often referred to as fuzzy PSI and is the focus of our work. Using a standard PSI protocol for this task leads to a rather inefficient solution since the communication and computation complexity usually scale at least linearly in the cardinality of the input sets, i.e., the total volume of the balls \(N\cdot \delta ^d\). Garimella et al. can overcome this barrier in terms of communication in the semi-honest [20] as well as in the malicious [21] setting. However, the receiver’s computation is still proportional to the total volume of the input balls, which makes their protocols scale poorly with the dimension d. Moreover, their protocols are limited to the \(L_{\infty }\) and \(L_1\)Footnote 1 distance and only realize a standard PSI functionality, where the receiver learns exactly which of the sender’s points lie in the intersection. Other works are either limited to the Hamming distance [37], Hamming and \(L_2\) distance [26] or Hamming distance and one-dimensional \(L_1\) distance [8], and often require heavy machinery or yield non-negligible correctness error.
In this work, we present fuzzy PSI protocols in the semi-honest setting for general \(L_\infty \) and \(L_{\textsf{p}}\) distance with \(\textsf{p}\in [1,\infty )\), and present several optimized variants for low as well as high dimensions. Notably, the communication as well as computation complexity of our high-dimension protocols scales linearly or quadratically with the dimension d. We moreover extend our protocols to various richer fuzzy PSI functionalities including PSI cardinality, labeled PSI, PSI with sender privacy, and circuit PSI. Our protocols have comparable performance to [20] in the low-dimensional setting and significantly outperform other approaches when the dimension increases. Finally, our protocols rely only on the decisional Diffie-Hellman (DDH) assumption.
1.1 Our Contributions
Fuzzy Matching. The main building block for our fuzzy PSI constructions is a fuzzy matching protocol, which on input a point \(\textbf{w}\in \mathbb {Z}^d\) from the receiver and a point \(\textbf{q}\in \mathbb {Z}^d\) from the sender, outputs 1 to the receiver if \(\textsf{dist}(\textbf{w},\textbf{q})\le \delta \) and 0 otherwise. Here \(\textsf{dist}\) can either be \(L_{\infty }\) distance or \(L_{\textsf{p}}\) distance for \(\textsf{p}\in [1,\infty )\). It results in a two-message protocol for \(L_{\infty }\) distance with communication complexity \(O(\delta d)\), computation complexity \(O(\delta d)\) for the receiver and O(d) for the sender when \(\textsf{dist}=L_\infty \); For \(L_\textsf{p}\) distance, it has communication complexity \(O(\delta d + \delta ^{\textsf{p}})\), computation complexity \(O(\delta d)\) for the receiver, and \(O(d +\delta ^{\textsf{p}})\) for the sender.
Fuzzy PSI in Low-Dimensions. Using a fuzzy matching protocol we can trivially obtain a fuzzy PSI protocol by letting the sender and receiver run the fuzzy matching protocol for every combination of inputs, but this leads to an undesirable \(N\cdot M\) blowup in communication and computation complexity. To circumvent this blowup for a low dimension d, we develop a new spatial hashing technique for disjoint \(L_\infty \) balls which incurs only a \(O(2^d)\) factor to the receiver’s communication and sender’s computational complexity. To support \(L_\textsf{p}\) balls, we extend the “shattering” idea from [20] to generalized \(L_\textsf{p}\) setting. The asymptotic complexities are given in Table 1. It is worth noting that, unlike to [20, 21], the computation complexity of our protocols scale sublinearly to the volume of balls.
Fuzzy PSI in High-Dimensions. Unfortunately, the above spatial hashing approaches still yield a \(2^d\) factor in the communication and computation complexities, which becomes prohibitive for large dimensions d. The earlier work [20] proposes a protocol that can overcome this factor, for communication costs, in the \(L_{\infty }\) setting under the globally disjoint assumption that the projections \([w_{k,i}-\delta ,w_{k,i}+\delta ]\) of the sender’s balls \(k\in [N]\) are disjoint for all dimensions \(i\in [d]\), which the authors themselves mention is a somewhat artificial assumption. We present a two-message protocol with comparable communication and much lower computation complexity under a milder assumption that for each \(k\in [N]\) there exists a dimension \(i\in [d]\) where the projection is disjoint from all other \(k'\in [N]\), namely, not necessary to be globally disjoint. We argue that this is a more realistic assumption since points in high dimensions tend to be sparser and show that it is satisfied with a high probability if the points \(\textbf{w}_k\) are uniformly distributed.
We moreover present a two-message protocol in the \(L_{\textsf{p}}\) setting which can circumvent this exponential factor in the dimension d, while achieving sub-quadratic complexity in the number of inputs. The key idea of this protocol is to use locality-sensitive hashing (LSH) to perform a coarse mapping such that points close to each other end up in the same bucket with high probability, and subsequently use our fuzzy matching protocol for \(L_{\textsf{p}}\) distance to compare the items in each bucket. See Table 1 for the asymptotic complexities of our protocols.
Extensions to Broader Functionalities. By default, all our protocols except for the LSH-based protocol realize the stricter PSI functionality where the receiver only learns how many of the sender’s points lie close to any of the receiver’s points, which we call PSI cardinality (PSI-CA). Earlier works [20, 21] realize the functionality where the receiver learns exactly which of the sender’s points are in the intersection. We refer to this functionality as standard PSI.
For all of our protocols discussed above, except for the LSH-based protocol, we show that we can extend them to realize the following functionalities: standard PSI; PSI with sender privacy (PSI-SP), where the receiver only learns which of the receiver’s balls are in the intersection; labeled PSI, where the receiver only learns some label associated to the sender’s points in the intersection; circuit PSI, where the parties only learn secret shares of the intersection and optional data associated to each input point, which they can use as the input to any secure follow-up computation. We can realize these extensions without increasing the asymptotic complexities of the protocols and without needing to introduce additional computational assumptions. With the only exception that for the circuit PSI extension we need a generic MPC functionality to compute a secure comparison circuit at the end of the protocol, which is common for traditional (non-fuzzy) circuit PSI protocols [34, 36].
Performance. Our experimental results demonstrate that it requires only \(1.2\) GB bandwidth and \(432\) s in total to complete a standard fuzzy PSI protocol when parties have thousands of \(L_\infty \) balls and millions of points in a \(5\)-dimensional space. As a comparison, prior works need \({\gg }{4300}\) s (conservative estimate).
1.2 Related Work
Traditional PSI protocols have become very efficient [9, 28, 35], but are optimized for the setting where the parties’ input sets have approximately the same size, and their communication and computation costs scale linearly with the input size. This leads to an inefficient fuzzy PSI protocol since the receiver’s input size is \(N\cdot \delta ^d\) when the receiver holds N hyperballs of dimension d and radius \(\delta \). Asymmetric (or unbalanced) PSI protocols [1, 10, 11, 14] target the setting where one party’s set is much larger than the other’s and can achieve communication complexity sublinear in the large set size, but \(O(\sqrt{N}\cdot \delta ^{d/2})\) computational complexity, using fully homomorphic encryption [14]. For traditional PSI there exist many efficient protocols realizing richer functionalities such as PSI cardinality [16, 27], labeled PSI [10, 14] and circuit PSI [24, 34, 36], but all of these suffer from the same limitations as discussed above when applied to the fuzzy PSI setting. There exists another line of works concerning threshold PSI [3, 7, 22, 23], where the fuzziness is measured by the number of exact matches between items.
Secure fuzzy matching was introduced by Freedman et al. [18] as the problem of identifying when two tuples have a Hamming distance below a certain threshold. They propose a protocol based on additively homomorphic encryption and polynomial interpolation, which was later shown to be insecure [12]. Follow-up works focus on the Hamming distance as well and use similar oblivious polynomial evaluation techniques [12, 38]. Indyk and Woodruff [26] construct a fuzzy PSI protocol for \(L_2\) and Hamming distance using garbled circuits. Uzun et al. [37] give a protocol for fuzzy labeled PSI for Hamming distance using garbled circuits and fully homomorphic encryption. Chakraborti et al. [8] propose a fuzzy PSI protocol for Hamming distance based on additively homomorphic encryption and vector oblivious linear evaluation (VOLE), which has a non-negligible false positive rate. They moreover present a protocol for one-dimensional \(L_1\) distance, which can be constructed using any O(N) communication PSI protocol for sets of size N, and has resulting communication complexity \(O(N\log {\delta })\) [8]. It is an interesting question whether their techniques can be extended to higher dimensions. Since the focus of our work is to construct fuzzy PSI protocols for general \(L_{\textsf{p}}\) and \(L_\infty \) distances, general dimension d, and with negligible error rate, it is not possible to make a meaningful comparison with these works.
Garimella et al. [20, 21] initiated the study of structure-aware PSI, which covers fuzzy PSI as a special case. They introduce the definition of weak boolean function secret sharing (bFSS) for set membership testing and give a general protocol for structure-aware PSI from bFSS. They develop several new bFSS techniques, focusing on the case where the input set is the union of N balls of radius \(\delta \) with respect to the \(L_{\infty }\) norm in d-dimensional space, which results in a fuzzy PSI protocol as the ones we concern ourselves with in this work. The techniques used in their protocols are fundamentally different from ours, except that we use similar spatial hashing techniques to obtain efficient fuzzy matching protocols in the low-dimensional setting. Moreover, their protocols are limited to the \(L_{\infty }\) and \(L_1\) distance setting and only realize the standard PSI functionality where the receiver learns the exact sender’s points in the intersection. Finally, the receiver’s computational complexity in their protocols scales as \(O((2\delta )^dN)\), which makes them unsuitable in the high-dimensional setting. See Table 1 for a more detailed comparison of communication and computational complexities.
1.3 Applications
Private Proximity Detection. There exist certain contexts where individuals need to know the proximity of others for varying purposes: In the realm of contact tracing, where individuals may seek to determine if they are in the vicinity of an infected person; Within the scope of ride-sharing platforms, users might wish to identify available vehicles in their surroundings. In both scenarios, the privacy of all involved parties should preserved and fuzzy PSI protocols provide a direct solution to this problem.
Biometric and Password Identification. Fuzzy matching could also be useful in authentication or identification scenarios. Notable applications of this technique can be observed in the matching of similar passwords to enhance usability or security. A case in point is Facebook’s authentication protocol, which auto-corrects the capitalization of the initial character in passwords [31]. Similarly, it can be useful to check if a user’s password is similar to a leaked password [33]. Furthermore, fuzzy matching can be employed to match biometric data, such as fingerprint and iris scans, thereby facilitating a blend of convenience and security [17]. In general, a fuzzy unbalanced PSI protocol is more useful since the server usually holds a large database of clients’ passwords (or biometric samples).
Illegal Content Detection. Recently, Bartusek et al. [4] introduced the study of illegal content detection within the framework of end-to-end secure messaging, focusing particularly on the detection of child sexual abuse material, encompassing photographs and videos. Central to their protocol is a two-message PSI protocol, wherein the initial message is reusable and published once for the receiver’s database. After this, the computational overhead for both parties is rendered independent of the database size. The research notably leverages Apple’s PSI protocol [5], which, while only facilitating exact matches, serves its purpose effectively. Ideally, matching should be sufficiently fuzzy to ensure that illegal images remain detectable even following rotation or mild post-processing. Our fuzzy PSI constructions, encapsulated within two-round protocols and featuring a reusable initial message, may find potential applicability in such contexts.
2 Technical Overview
Before heading for the details of our fuzzy matching and PSI protocols, let us start by discussing a standard PSI protocol proposed by Apple [5].
2.1 Recap: Apple’s PSI Protocol
We simplify Apple’s PSI protocol to the basic setting where the receiver holds a set \(W:=\{w_1,\dots ,w_n\}\), the sender holds an item \(q\), and the receiver wants to learn \(q\) if \(q\in W\) and nothing otherwise. Their main idea is a novel usage of random self-reduction of DDH tuples from Naor and Reingold [32] in PSI contexts. Given a cyclic group \(\mathbb {G}:=\langle g\rangle \) of prime order \(p\), the tuple \((g,h,h_1,h_2)\) can be re-randomized into \((g,h,u,v)\) such that \(u,v\) are uniformly random over \(\mathbb {G}\) as long as \((g,h,h_1,h_2)\) is not a well-formed DDH tuple (i.e., there is no \(s\in \mathbb {Z}_p^*\) to satisfy \(g^s=h \wedge h_1^s=h_2\)). Otherwise, both \((g,h,h_1,h_2)\) and the re-randomized tuple \((g,h,u,v)\) are valid DDH tuples. This re-randomization basically utilizes two random coins
 to output
to output
Now to obtain a PSI protocol, the receiver could sample
 and publish
and publish
where \(\textsf{H}\) is a hash-to-group function. Then the sender returns pairs
where \((u_i,v_i)\) is the re-randomization output for each tuple \(\left( g,h,\textsf{H}(q),\textsf{H}(w_i)^s\right) \), and \(\textsf{Enc}\) is some symmetric-key encryption scheme (e.g., a one-time pad). The receiver can try to decrypt each \(\textsf{ct}_i\) using the key \(u_i^s\) to learn \(q\). For the sender’s privacy, the random self-reduction of DDH tuples guarantees that when \(q\ne w_i\), the secret key \(v_i\) is uniformly random from the receiver’s view and thus \(q\) is hidden according to the security of this symmetric-key encryption. For the receiver’s privacy, \(\left( \textsf{H}(w_1)^s,\dots ,\textsf{H}(w_n)^s\right) \) is pseudorandom according to the generalized DDH assumption when \(\textsf{H}\) is modelled as a random oracle.
2.2 Fuzzy Matching for Infinity Distance
Our crucial observation is that the above approach can be naturally applied in fuzzy matching protocols where the receiver holds a point \(\textbf{w}\in \mathbb {Z}^d\) in a \(d\)-dimensional space, the sender holds a point \(\textbf{q}\in \mathbb {Z}^d\), and the receiver learns if \(\textsf{dist}(\textbf{w},\textbf{q})\le \delta \). Here, \(\delta \) is the maximal allowed distance between \(\textbf{w}\) and \(\textbf{q}\). For the moment, let us focus on the simplest case where the distance is calculated over \(L_\infty \), which means, the receiver gets \(1\) if
and gets \(0\) otherwise. This problem is equivalent to the following: The receiver holds \(d\) sets \(\{W_1,\dots , W_d\}\) where \(W_i:=\{w_i-\delta ,\dots ,w_i+\delta \}\), the sender holds \(d\) items \(\{q_1,\dots ,q_d\}\), and they want to run a membership test for each dimension simultaneously, without leaking the results for individual dimensions. Though the receiver can publish \(\textsf{H}(w_i+j)^s\) for each \(i\in [d],j\in [-\delta ,+\delta ]\) as above, the sender has to use random self-reduction for each possible match, which yields too much communication and computation effort for the sender. Namely, the entire volume of a \(d\)-dimensional \(\delta \)-radius ball \(O\left( (2\delta +1)^d\right) \).
Reducing the Complexity. There is a standard trick to significantly reduce the complexity by using an oblivious key-value store (\(\textsf{OKVS}\)). Recall that an \(\textsf{OKVS}\) [19] will encode a key-value list \(\{(\textsf{key}_j,\textsf{val}_j)\}_{j\in [n]}\) into a data structure \(E\), such that decoding with a correct \(\textsf{key}_*\) returns the corresponding \(\textsf{val}_*\), where the encoding time scales linearly to the list size and decoding a single key takes only a constant number of operations. So the above protocol can be improved as follows:
-
1)
The receiver publishes \(\left( g,h,E_i\leftarrow \textsf{Encode}(\{(w_i+j,\quad \textsf{H}(w_i+j)^s)\}_{j\in [-\delta ,+\delta ]})\right) \) for each \(i\in [d]\);
-
2)
The sender retrieves \(h_i\leftarrow \textsf{Decode}(E_i,q_i)\) for each \(i\in [d]\) and sends the rerandomized tuple \((u:=g^a\prod _{i=1}^d \textsf{H}(q_i)^b,v:=h^a\prod _{i=1}^d h_{i}^b)\), where
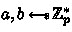 , to the receiver;
, to the receiver; -
3)
The receiver checks if \((g,h,u,v)\) is a valid DDH tuple.
The protocol is correct when \(\textsf{dist}(\textbf{q},\textbf{w})\le \delta \), according to the correctness of the underlying \(\textsf{OKVS}\) scheme, which says that decoding the structure \(E_i\) with a correct encoding key \(q_i\) will return the encoded value \(h_i:=\textsf{H}(q_i)^s\); When \(\textsf{dist}(\textbf{q},\textbf{w})>\delta \), we typically need to rely on the independence property of \(\textsf{OKVS}\), which says that decoding with a non-encoded key will yield a uniformly random result. Therefore, in this case, there exists at least one \(h_{i^*}\) that is uniformly random; hence \((g,h,\textsf{H}(q_{i^*}), h_{i^*})\) is not a DDH tuple except with negligible probability. The sender’s privacy can be established as before from the random self-reduction of DDH tuples. To argue the receiver’s privacy, we rely on the obliviousness property of the \(\textsf{OKVS}\), namely, the encoded keys \(\{w_i+j\}\) are completely hidden as long as the encoded values \(\{\textsf{H}(w_i+j)^s\}\) are uniformly random. Since \((h,\textsf{H}(w_i+j),\textsf{H}(w_i+j)^s)\) is pseudorandom by the DDH assumption, then according to the obliviousness of \(\textsf{OKVS}\), the receiver’s message can be simulated by encoding random key-value pairs.
Note that our real construction shown in Sect. 5.1, is slightly different from what we described here. We encode the \(\textsf{OKVS}\) “over the exponent” to reduce heavy public-key operations over \(\mathbb {G}\) because our encoded values are pseudorandom over a structured group \(\mathbb {G}\) (i.e., the elliptic curves).
So far, we have obtained a two-message fuzzy matching protocol for \(L_\infty \) distance, with \(O(d\delta )\) communication and computation complexity.
2.3 Generalized Distance Functions
When the distance function is calculated in \(L_\textsf{p}\), the receiver would get \(1\) if
and \(0\) otherwise. To make the problem easier, we consider the \(\textsf{p}\)-powered \(L_\textsf{p}\) distance, namely, we check if \(\sum _{i=1}^d |w_i-q_i|^\textsf{p}\le \delta ^\textsf{p}\). Thanks to the homomorphism of DDH tuples, the sender can homomorphically evaluate the distance function. Moreover, since an \(L_{\textsf{p}\ge 1}\) ball must be confined in an \(L_\infty \) ball, namely, \(|w_i-q_i|\le \delta \) for any \(i\in [d]\) if \(\textsf{dist}_\textsf{p}(\textbf{w},\textbf{q})\le \delta \), the protocol could work as follows:
-
1)
The receiver publishes
$$\begin{aligned} \Bigg (g,h,E_i\leftarrow \textsf{Encode}\bigg (\Big \{\big (w_i+j,\quad \textsf{H}(w_i+j)^s\cdot g^{|j|^\textsf{p}}\big )\Big \}_{j\in [-\delta :\delta ]}\bigg )\Bigg ), \end{aligned}$$for each \(i\in [d]\);
-
2)
The sender retrieves \(h_i\leftarrow \textsf{Decode}(E_i,q_i)\) for each \(i\in [d]\), and computes
$$\begin{aligned} \left( u:=g^a\prod _{i=1}^d \textsf{H}(q_i)^b, v:=h^a\prod _{i=1}^d h_i^b\right) , \end{aligned}$$for random
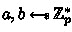 ;
; -
3)
The sender generates a list \(\textsf{list}:=\{g^{b\cdot j}\}_{j\in [0:\delta ^\textsf{p}]}\) and outputs \((u,v,\textsf{list})\);
-
4)
The receiver checks if there is any \(x\in \textsf{list}\) such that \(v=u^s\cdot x\).
Denote \(t:=\textsf{dist}_\textsf{p}(\textbf{w},\textbf{q})\). If \(\forall i\in [d],\,|w_i-q_i|\le \delta \), then the correctness holds naturally since each retrieved \(h_i:=\textsf{H}(q_i)^s\cdot g^{|w_i-q_i|^\textsf{p}}\), implying that
which would be included in \(\textsf{list}\) if and only if \(t\le \delta \)Footnote 2. On the other hand, if there exists \(i^*\in [d]\) such that \(|w_{i^*}-q_{i^*}|>\delta \), then according to the independence property of \(\textsf{OKVS}\) the decoded \(h_{i^*}\) as well as \(v\) would be uniformly random over \(\mathbb {G}\), such that \(v/u^s\in \textsf{list}\) with only negligible probability.
Subtle Issues and the Fix. The receiver’s privacy is almost the same as before, relying on the generalized DDH assumption and the obliviousness of \(\textsf{OKVS}\). It is a little bit subtle to argue the sender’s privacy: Currently, \(\textsf{list}\) would leak information on the sender’s input. Precisely, given \((u,v,\textsf{list})\), the receiver could check, for example, if \(\frac{v}{u^s\cdot g^b}\in \textsf{list}\) to learn if \(t^\textsf{p}=\delta ^\textsf{p}+1\) or not, since \(g^b\in \textsf{list}\). Moreover, even in the case that \(t\le \delta \), the receiver could still deduce the exact \(t\) by checking which index is matched. The latter can be solved by shuffling the \(\textsf{list}\), so we focus on the former issue. One approach is to hash each list item as \(\textsf{list}:=\{\textsf{H}'(g^{b\cdot j})\}_{j\in [0:\delta ^\textsf{p}]}\). By modeling \(\textsf{H}':\mathbb {G}\mapsto \{0,1\}^*\) as a random oracle, the group structure is erased and the adversary cannot utilize \(g^{b\cdot j}\) anymore. However, the issue still exists since the adversary could check if \(\textsf{H}'\big ((\frac{v}{u^s})^{1/\alpha }\big )\in \textsf{list}\) to learn if \(t^\textsf{p}\in \{0,\alpha ,2\alpha ,\dots ,\delta ^\textsf{p}\alpha \}\) for any \(\alpha \). Therefore, we have to apply a random linear function over \(t^\textsf{p}\) to make sure that \(\frac{v}{u^s}=g^{b\cdot t^\textsf{p}+c}\) where \(b,c\) are random scalars. The details can be found in Sect. 5.2.
Regarding the complexity, the communication and computation are increased by an additive term \(O(\delta ^\textsf{p})\) from the infinity distance setting.
2.4 Fuzzy PSI in Low Dimensions
For the moment, let us consider the fuzzy PSI cardinality problem, where the receiver holds a union of \(d\)-dimensional balls of radius \(\delta \) represented by their centers \(\{\textbf{w}_1,\dots ,\textbf{w}_N\}\), the sender holds a set of points \(\{\textbf{q}_1,\dots ,\textbf{q}_M\}\) in the same space, and the receiver learns the number of sender’s points located inside the balls. When the dimension \(d\) of the space is low, e.g., \(O(\log (\lambda ))\), we can exploit the geometric structure of the space to efficiently match balls and points to avoid the quadratic blowup mentioned in the introduction. The high-level idea is to tile the entire space by \(d\)-dimensional hypercubes of side-length \(2\delta \) (also called cells, together a grid), then the receiver can encode a ball (represented by its center \(\textbf{w}_i\)) in a way that the sender can efficiently match it with a point \(\textbf{q}_j\), without enumerating all balls. After that, both parties can run a fuzzy matching protocol between \(\textbf{w}_i\) and \(\textbf{q}_j\) as before.
The idea of Garimella et al. [20] is to “shatter” each receiver’s ball into its intersected cells, however, to guarantee each cell is intersected with a single ball (otherwise collisions appear during encoding an \(\textsf{OKVS}\)Footnote 3), the receiver’s balls typically need to be at least \(4\delta \) apart from each other. To tackle the case of disjoint balls, the authors improved their techniques [21] by observing that each grid cell can only contain the center of a single receiver’s ball. Thus, the receiver could encode the identifier of each cell which contains a ball center, and the sender can try to decode the \(\textsf{OKVS}\) by iterating over all neighborhood cellsFootnote 4 surrounding its point. This approach yields a \(O(3^d)\) factor for the sender’s computation and communication costs: Given a point \(\textbf{q}\), the center of any \(L_\infty \) ball intersected with \(\textbf{q}\) is located in at most \(3^d\) cells surrounding the cell containing \(\textbf{q}\).
New Spatial Hashing Ideas. Here we provide a new hashing technique to reduce this blowup from \(3^d\) to \(2^d\). Note that the \(3^d\) factor comes from the fact that the entire neighborhood of the point \(\textbf{q}\) is too large (i.e., a hypercube of side-length \(6\delta \)), but we only need to care about the neighbor cells that intersected with the receiver’s balls already. Specifically, if the grid is set properly, an \(L_\infty \) ball will intersect exactly \(2^d\) cells, which constitute a hypercube of side-length \(4\delta \), denoted as a block. Our crucial observation is that each block is unique for each disjoint ball, i.e., two disjoint balls must be associated with different blocks, as detailed in Lemma 6. Given this, the receiver could encode the identifier of each block, and the sender would decode by iterating all potential blocks. There are in total \(2^d\) possible blocks for each sender’s point due to each block being comprised of \(2^d\) cells and each cell contains at most a single ball’s center.
Compatible with \(\boldsymbol{L_\textsf{p}}\) Balls. Though we only considered \(L_\infty \) balls so far, we can generalize the “shattering” idea from [20] to \(L_\textsf{p}\) balls as well. We still tile the space with hypercubes, but we show that as long as \(L_\textsf{p}\) balls are at least \(2\delta (d^{1/\textsf{p}}+1)\) apart from each other, then each grid cell intersects at most one \(L_\textsf{p}\) ball, as detailed in Lemma 5. Particularly, when \(\textsf{p}=\infty \), \(2\delta (d^{1/\textsf{p}}+1)\) degrades to the original \(4\delta \). Combining it with our fuzzy matching protocols for \(L_\textsf{p}\) distance, we immediately obtain fuzzy PSI for precise \(L_\textsf{p}\) distance (i.e., without approximation or metric embedding). One important step different from the \(L_\infty \) setting is to pad the key-value list to size \(2^d N\) with random pairs since an \(L_\textsf{p}\) ball could intersect with a various number of cells. Otherwise, the receiver’s privacy would be compromised.
2.5 Extending to High Dimensions
To overcome the \(2^d\) factor in complexities, we first focus our attention on \(L_\infty \) distances: Ideally, if the receiver’s balls are globally disjoint on every dimension, namely, the projection of the balls on each dimension never overlaps, then the “collision” issue mentioned above would disappear. In this way, for each dimension \(i\in [d]\), the receiver could encode the \(\textsf{OKVS}\) as
where \(w_{k,i}\) is the projection of the ball center \(\textbf{w}_k\) on dimension \(i\). The sender just behaves the same as in Sect. 2.2. This approach results in \(O(\delta dN+M)\) communication and computation costs. However, as stated in [20], this ideal setting is somewhat artificial and unrealistic.
Weaker Assumptions by Leveraging Dummy OKVS Instances. After taking a closer look at this approach, we realized that the global disjointness is not necessary to be satisfied on every dimension, as we actually could tolerate some collisions. Specifically, the value \(h_i\) decoded from \(E_i\) for some point \(\textbf{q}\) (lying in one of the receiver’s balls) would constitute a tuple \(\left( g,h,\textsf{H}(q_i), h_i\right) \). However, this tuple does not necessarily need to be a DDH tuple. We only need the final product
to be a valid DDH tuple for correctness.
Suppose there exists at least one dimension on which the projections of all balls are disjoint. This gives each ball a unique way to identify it from others. Our idea is to leverage \(\textsf{OKVS}\) instances recursively: For each ball \(\textbf{w}_k\), the receiver encodes an outer \(\textsf{OKVS}\) for dimension \(i\) by
where \(\textsf{val}_{k,i,j}\) differs in two cases:
-
If the current dimension \(i\) is the globally separated dimension for all balls, then \(\textsf{val}_{k,i,j}\) is an inner \(\textsf{OKVS}\) instance for fuzzy matching with \(\textbf{w}_k\), namely,
$$\begin{aligned} \textsf{val}_{k,i,j}\leftarrow \textsf{Encode}\Big (\Big \{\big (i'\,\Vert \,w_{k,i'}+j',\quad h_{i',j'}\,\Vert \,h^s_{i',j'}\big )\Big \}_{i'\in [d],j'\in [-\delta ,+\delta ]}\Big ), \end{aligned}$$where
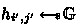 ;
; -
Otherwise, the \(\textsf{val}_{k,i,j}:=(\textbf{r}\,\Vert \,\textbf{r}^s)\) is a dummy instance where
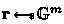 and \(m\) is the size of the inner \(\textsf{OKVS}\) instance.
and \(m\) is the size of the inner \(\textsf{OKVS}\) instance.
For each point \(\textbf{q}\), the sender first decodes the outer \(\textsf{OKVS}\) to obtain a list \(\{\textsf{val}_1,\dots ,\textsf{val}_d\}\), then runs the decoding function on each \(\textsf{val}_{j\in [d]}\) to get
In the end, the sender re-randomizes the result from the tuple \((g,h,\prod _{j=1}^d u_j, \prod _{j=1}^d v_j)\).
For correctness, we expect that decoding a dummy instance on any key would output a valid DDH pair all the time. This can be guaranteed if the inner \(\textsf{OKVS}\) has a linear decoding function. Clearly, in this way, each \(\textbf{q}\) would get either an inner \(\textsf{OKVS}\) instance or random garbage from the globally separated dimension. The latter results in valid DDH tuples with negligible probability, so we focus on the case that the sender gets an inner \(\textsf{OKVS}\) instance in the end. This reduces the fuzzy PSI problem to the fuzzy matching problem as other dummy instances won’t affect the correctness. For security, the inner \(\textsf{OKVS}\) has to be doubly oblivious, namely, the encoded structure itself is uniformly random. Regarding the complexity, the receiver’s communication and computation costs would be \(O(d\delta )\) times larger.
Further Weaken the Assumption. The above assumption is weaker and milder than what was used in prior works, but it is still somewhat artificial. Here we show that we can even weaken this assumption to the following: For each ball, there exists at least one dimension on which its projection is separated from others. Note that the above approach doesn’t work yet in this setting: There might exist a point whose projection on each dimension is inside the projection of a non-separated interval from some ball. In other words, the sender would get a list of dummy instances after decoding the outer \(\textsf{OKVS}\). This results in a false positive since dummy instances always output a match. To rule out these false positives, we realize that we could encode additional information into each \(\textsf{val}_{k,i,j}\).
For simplicity, let’s assume the decoding function of the \(\textsf{OKVS}\) is determined by a binary vector with some fixed hamming weight, that is, given an instance \(\textbf{r}\in \mathbb {G}^m\) and some \(\textsf{key}\), the decoding function outputs
where \(\textbf{d}\in \{0,1\}^m\) is deterministically sampled by the \(\textsf{key}\), and \(\textsf{HammingWeight}(\textbf{d})=t\). The receiver samples two random shares \(\zeta _\bot ,\zeta _\top \) such that \(\zeta _\bot \cdot \zeta _\top =1\). We denote as \(I_k\) the first dimension on which \(\textbf{w}_k\) projects a separated interval. Then the receiver could set \(\textsf{val}_{k,i,j}\) for each \(\textbf{w}_k\) in this way:
-
If the current dimension \(i=I_k\), then \(\textsf{val}_{k,i,j}\) is an inner \(\textsf{OKVS}\) instance defined by
$$\begin{aligned} \textsf{val}_{k,i,j}\leftarrow \textsf{Encode}\Big (\Big \{\big (i'\,\Vert \,w_{k,i'}+j',\quad h_{i',j'}\,\Vert \,h^s_{i',j'}\cdot \zeta _\bot ^{t\cdot (d-1)}\big )\Big \}_{i'\in [d],j'\in [-\delta ,+\delta ]}\Big ), \end{aligned}$$where
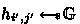 and \(t\) is the hamming weight of \(\textbf{d}\);
and \(t\) is the hamming weight of \(\textbf{d}\); -
Otherwise, the \(\textsf{val}_{k,i,j}:=(\textbf{r}\,\Vert \,\textbf{r}^s\cdot \zeta _\top )\) for
 .
.
The security follows as before, whereas the correctness is non-trivial. First, consider the sender’s point \(\textbf{q}\) intersecting some receiver’s ball. After decoding the inner \(\textsf{OKVS}\) instance, the sender gets a pair \((u_*\,\Vert \,u_*^s\cdot \zeta _\bot ^{td\cdot (d-1)})\) for some \(u_*\); After decoding a dummy instance, the sender gets \((r_*\,\Vert \,r_*^s\cdot \zeta _\top ^{td})\) for some \(r_*\) instead. Now, by multiplying them together, the final tuple
is a valid DDH tuple for some \(v\in \mathbb {G}\).
Then consider the case that the sender’s point \(\textbf{q}\) is outside of all balls. The only way to report a match is to get a list of all dummy instances after decoding the outer \(\textsf{OKVS}\) instance, otherwise the inner \(\textsf{OKVS}\) instance will output a random garbage result. However, since dummy instances only encode \(\zeta _\top \), the product of them equals \(1\) with negligible probability due to \(\zeta _\top \) being randomly sampled and \(td^2\ll p\) if \(t=O(\kappa )\).
Recall that we assume the decoding vector \(\textbf{d}\) to have fixed hamming weight. This is not ideal since most modern \(\textsf{OKVS}\) instantiations (e.g., [6, 19, 35]) don’t satisfy this requirement, whereas the only exception is the garbled bloom filters [15] whose efficiency is not satisfactory. We managed to get rid of this assumption in our real protocol in the end, please refer to Sect. 7.1 for details.
Locality-Sensitive Hashing. The above approaches are heavily tailored to the \(L_\infty \) distance. To support \(L_\textsf{p}\) distance in high dimensions, we utilize locality-sensitive hashing (LSH) to identify matching balls. An LSH family with parameters \((\delta , c\delta ,p_1,p_2)\) guarantees the following:
-
If two points \(\textbf{w}\) and \(\textbf{q}\) are close enough, i.e., \(\textsf{dist}_\textsf{p}(\textbf{w},\textbf{q})\le \delta \), they would be hashed into the same bucket with at least \(p_1\) probability;
-
If they are far apart, i.e., \(\textsf{dist}_\textsf{p}(\textbf{w},\textbf{q})>c\delta \), then the probability of hashing them into the same bucket is at most \(p_2\).
In other words, an LSH family bounds the false-positive and false-negative probability to \(p_2\) and \(1-p_1\), respectively. Usually, false-positive and false-negative cannot be reduced to negligible simultaneously. However, given the existence of our fuzzy matching protocols, we can tolerate false positives by running fuzzy matching on each positive match. Therefore, the high-level strategy is that the receiver hashes each ball center via LSH to some LSH entry, and the sender would identify multiple positive LSH entries for each of its points. If we set the parameters properly, the total number of false positives for each sender’s point can be upper-bounded by \(O(N^\rho )\) for some \(\rho <1\) which gives us just a sub-quadratic blowup in total communication and computation complexities.
One caveat is that there is a constant gap between the calculation of false positives and false negatives mentioned above, namely, false positives are calculated when points are \(c\delta \)-apart, whereas false negatives are calculated when points are \(\delta \)-close. Fortunately, when the receiver’s balls are disjoint (i.e., centers are \(2\delta \)-part), this gap can be filled by setting \(c=2\). Another caveat is that this approach does not support fuzzy PSI cardinality anymore due to the rationale behind the LSH: To guarantee a negligible false-negative rate, we typically have to prepare multiple LSH tables where a true positive might appear more than once.
For the formal details of this construction, we refer to the full version of the paper [2].
3 Preliminaries
We represent the computational security parameter as \(\lambda \in \mathbb {N}\), the statistical security parameter as \(\kappa \in \mathbb {N}\) and the output of the algorithm \(\mathcal {A}\) on input \(\textsf{in}\) using \(r \leftarrow \{0,1\}\) as its randomness by \(x \leftarrow \mathcal {A}(\textsf{in};r)\). The randomness is often omitted and only explicitly mentioned when necessary. Efficient algorithms are considered to be probabilistic polynomial time (PPT) machines. We use \(\approx _c\) to denote computational indistinguishability and \(\approx _s\) to denote statistical indistinguishability of probability distributions. The notation [n] signifies a set \(\{1,\dots ,n\}\) and [a : b] the set \(\{a,a+1,\dots b-1,b\}\). We use \(\textbf{c}[i:j]\) to represent a vector with a defined length of \([c_i,\dots ,c_j]\) and \(\textbf{c}\) to indicate a vector of c.
All the protocols presented in this work are two-party protocols. Security is proven against semi-honest adversaries via the standard simulation-based paradigm (see e.g., [29]).
3.1 Oblivious Key-Value Store (OKVS)
The concept of an oblivious key-value store (\(\textsf{OKVS}\)) was introduced by Garimella et al. [19] to capture the properties of data structures commonly used in PSI protocols. Subsequent works proposed \(\textsf{OKVS}\) constructions offering favorable trade-offs between encoding/decoding time and encoding size [6, 35].
Definition 1
(Oblivious Key-Value Store). An oblivious key-value store \(\textsf{OKVS}\) is parameterized by a key space \(\mathcal {K}\), a value space \(\mathcal {V}\), computational and statistical security parameters \(\lambda ,\,\kappa \), respectively, and consists of two algorithms:
-
\(\textsf{Encode}:\) takes as input a set of key-value pairs \(L\in (\mathcal {K}\times \mathcal {V})^n\) and randomness \(\theta \in \{0,1\}^{\lambda }\), and outputs a vector \(P\in \mathcal {V}^{m}\) or a failure indicator \(\bot \).
-
\(\textsf{Decode}:\) takes as input a vector \(P\in \mathcal {V}^m\), a key \(k\in \mathcal {K}\) and randomness \(\theta \in \{0,1\}^{\lambda }\), and outputs a value \(v\in \mathcal {V}\).
That satisfies:
-
Correctness: For all \(L\in (\mathcal {K}\times \mathcal {V})^n\) with distinct keys and \(\theta \in \{0,1\}^{\lambda }\) for which \(\textsf{Encode}(L;\theta )=P\ne \bot \), it holds that \(\forall (k,v)\in L\): \(\textsf{Decode}(P,k;\theta )=v\).
-
Low failure probability: For all \(L\in (\mathcal {K}\times \mathcal {V})^n\) with distinct keys:

-
Obliviousness: For any \(\{k_1,\dots ,k_n\},\,\{k_1',\dots ,k_n'\}\subseteq \mathcal {K}\) of n distinct keys and any \(\theta \in \{0,1\}^{\lambda }\), if \(\textsf{Encode}\) does not output \(\bot \), then for
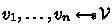 : \(\{P\leftarrow \textsf{Encode}(\{(k_i,v_i)_{i\in [n]})\};\theta )\} \approx _c \{P'\leftarrow \textsf{Encode}(\{(k'_i,v_i)_{i\in [n]}\};\theta )\}.\)
: \(\{P\leftarrow \textsf{Encode}(\{(k_i,v_i)_{i\in [n]})\};\theta )\} \approx _c \{P'\leftarrow \textsf{Encode}(\{(k'_i,v_i)_{i\in [n]}\};\theta )\}.\) -
Double obliviousness: For all sets of n distinct keys \(\{k_1,\dots ,k_n\}\subseteq \mathcal {K}\) and n values
 , there is \(\textsf{Encode}(\{(k_i,v_i)_{i\in [n]})\};\theta )\}\) statistically indistinguishable from uniformly random element from \(\mathcal {V}^m\).
, there is \(\textsf{Encode}(\{(k_i,v_i)_{i\in [n]})\};\theta )\}\) statistically indistinguishable from uniformly random element from \(\mathcal {V}^m\).
The efficiency of \(\textsf{OKVS}\) is characterized by: (1) the time it takes to encode n key-value pairs; (2) the time it takes to decode a single key; (3) the ratio n/m between the number of key-value pairs n and the encoding size m, also called the rate. Recent \(\textsf{OKVS}\) constructions [6, 19, 35] achieve: (1) encoding time \(O(n\kappa )\); (2) decoding time \(O(\kappa )\); (3) constant rate.
For this work, we will need \(\textsf{OKVS}\) to support the value space \(\mathcal {V}\) being equal to a cyclic group \(\mathbb {G}\) of prime order p. A sufficient condition for this, which is satisfied by the efficient constructions of [6, 19, 35] is:
-
\(\mathbb {F}_p\)-Linear: There exists a function \(\textsf{dec}:\mathcal {K}\times \{0,1\}^{\lambda }\rightarrow \mathbb {F}_p^m\) such that for all \(P\in \mathbb {G}^m\), \(k\in \mathcal {K}\) and \(\theta \in \{0,1\}^{\lambda }\) it holds that \(\textsf{Decode}(P,k;\theta ):=\langle \textsf{dec}(k;\theta ), P\rangle \), where for \(\textbf{d}\in \mathbb {F}_p^m\) and \(\textbf{g}\in \mathbb {G}^m\) we define \(\langle \textbf{d},\textbf{g}\rangle := g_1^{d_1} \cdots g_m^{d_m}\).
Lemma 1
(Independence). If \(\textsf{OKVS}\) satisfies \(\mathbb {F}_p\)-linearity and \(\textsf{negl}\!\!\left( \kappa \right) \) failure probability, and \(\theta \) is uniformly randomly chosen, then for any \(L:=\{(k_i,v_i)_{i\in [n]}\}\) with distinct keys, and any key \(k\notin \{k_i\}_{i\in [n]}\), it holds that \(\textsf{Decode}\left( \textsf{Encode}( L; \theta ),k\right) \) is indistinguishable from random.
3.2 Random Self-reductions of DDH Tuples
The well-known decisional Diffie-Hellman (DDH) assumption for a cyclic group \(\mathbb {G}=\langle g\rangle \) of prime order p states that the distribution of Diffie-Hellman (DH) tuples \((g,h:=g^s,h_1,h_2:=h_1^{s})\), where
 ,
,
 , is computationally indistinguishable from the distribution of random tuples \((g,h:=g^s,h_1,h_2)\), where
, is computationally indistinguishable from the distribution of random tuples \((g,h:=g^s,h_1,h_2)\), where
 ,
,
 . Naor and Reingold [32] show that deciding whether an arbitrary tuple \((g,h,h_1,h_2)\) with \(h,h_1,h_2\in \mathbb {G}\) is a DH tuple can be reduced to breaking the DDH assumption. For this work, we consider a special case of this reduction where \(h:=g^s\) is fixed.
. Naor and Reingold [32] show that deciding whether an arbitrary tuple \((g,h,h_1,h_2)\) with \(h,h_1,h_2\in \mathbb {G}\) is a DH tuple can be reduced to breaking the DDH assumption. For this work, we consider a special case of this reduction where \(h:=g^s\) is fixed.
Lemma 2
(Random Self-Reduction [32]). Let \(\mathbb {G}:=\langle g\rangle \) be a cyclic group of order p, let \(h:=g^s\) for \(s\in \mathbb {Z}_p\) and \(h_1,h_2\in \mathbb {G}\). If \(h_1':=g^a\cdot h_1^b\) and \(h_2':=h^a\cdot h_2^b\), where
 , then:
, then:
-
\(h_1'\) is uniformly random in \(\mathbb {G}\) and \(h_2'=(h'_1)^s\) if \(h_2=h_1^s\).
-
\((h_1',h_2')\) is a uniformly random pair of group elements otherwise.
4 Definitions and Functionalities
We define the two-message protocol as below, consisting of three algorithms:
-
\(\textsf{Receiver}_1(\textsc {Input}_R)\): The algorithm takes the \(\textsc {Receiver}\)’s \(\textsc {Input}_R\), outputs the first message \(\textsf{msg}_1\) and its secret state \(\textsf{st}\);
-
\(\textsf{Sender}_1(\textsc {Input}_S,\textsf{msg}_1)\): The algorithm takes the \(\textsc {Sender}\)’s \(\textsc {Input}_S\) and \(\textsf{msg}_1\), outputs the second message \(\textsf{msg}_2\);
-
\(\textsf{Receiver}_2(\textsf{st},\textsf{msg}_2)\): The algorithm takes the state \(\textsf{st}\) and the second message \(\textsf{msg}_2\), outputs the final \(\textsc {Output}\).
4.1 Definition of Fuzzy Matching
We define the functionality of fuzzy matching between two points in Fig. 1, with different distance functions including both infinity (\(L_\infty \)) and Minkowski (\(L_{\textsf{p}}\)) distance where \(\textsf{p}\in [1,\infty )\).
4.2 Definition of Fuzzy (Circuit) Private Set Intersection
We define the functionality of fuzzy PSI and fuzzy circuit PSI in Figs. 2 and 3, respectively. Note that for standard fuzzy PSI, we also consider a slightly stronger functionality (compared to prior works) where the receiver only learns whether their points are in the intersection, but not the sender’s exact points, which we call PSI with sender privacy (PSI-SP). We extend the functionality of fuzzy PSI to many closely related variants including PSI cardinality (PSI-CA), labeled PSI, and circuit PSI.
5 Fuzzy Matching
We start by presenting a fuzzy matching protocol for two points in hyperspace with infinity distance (\(L_\infty \)) and hamming distance, then we extend it into a more general setting with Minkowski distance (\(L_{\textsf{p}\in [1,\infty )}\)).
5.1 Fuzzy Matching for Infinity Distance
We provide the protocol for infinity distance in Fig. 4. We also show how to generalize the above approach to support the conjunction of infinity and hamming distance in the full version of the paper [2]. The proofs of the following theorems can be found in the full version of the paper [2].
Theorem 1
(Correctness). The protocol provided in Fig. 4 is correct with \(1-\textsf{negl}\!\!\left( \kappa \right) \) probability if \(\textsf{OKVS}\) satisfies perfect correctness defined in Sect. 3.1 and independence property from Lemma 1, and \(\textsf{H}_\gamma :\{0,1\}^*\mapsto \{0,1\}^{\gamma },\textsf{H}_{\kappa '}:\mathbb {G}\mapsto \{0,1\}^{\kappa '}\) are universal hash functions where \(\gamma =\kappa +\log \delta \) and \(\kappa '=\kappa \).
Theorem 2
(Security). The protocol provided in Fig. 4 realizes the functionality defined in Fig. 1 for \(L_\infty \) distance function against semi-honest adversaries if \(\textsf{OKVS}\) is oblivious and the DDH assumption holds.
Theorem 3
(Complexity). The communication complexity is \(O\left( 2\delta d\lambda +\right. \)\(\left. \lambda +\kappa \right) \) where \(\lambda ,\kappa \) are the security and statistical parameters; The computational complexity is \(O(2\delta d)\) for the receiver and O(d) for the sender.
5.2 Fuzzy Matching for Minkowski Distance
We provide the protocol for \(L_\textsf{p}\) distance where \(1\le \textsf{p}<\infty \) in Fig. 5. For simplicity, we assume \(\textsf{p}\) is an integer for the moment. The proofs of the following theorems can be found in the full version of the paper [2].
Theorem 4
(Correctness). The protocol provided in Fig. 5 is correct with \(1-\textsf{negl}\!\!\left( \kappa \right) \) probability if \(\textsf{OKVS}\) satisfies perfect correctness defined in Sect. 3.1 and independence property from Lemma 1, and \(\textsf{H}_\gamma :\{0,1\}^*\mapsto \{0,1\}^\gamma ,\textsf{H}_\kappa :\mathbb {G}\mapsto \{0,1\}^\kappa \) are universal hash functions where \(\gamma = \kappa +\log \delta \) and \(\kappa '=\kappa +\textsf{p}\log \delta \).
Theorem 5
(Security). The protocol provided in Fig. 5 realizes the functionality defined in Fig. 1 for \(L_\textsf{p}\) distance function, against semi-honest adversaries if \(\textsf{OKVS}\) is oblivious, the hash function \(\textsf{H}_{\kappa '}:\mathbb {G}\mapsto \{0,1\}^{\kappa '}\) is modeled as a random oracle, and the DDH assumption holds.
Theorem 6
(Complexity). The communication complexity is \(O(2\delta d\lambda +2\lambda +\delta ^\textsf{p}\kappa )\) where \(\lambda ,\kappa \) are the security and statistical parameters; The computational complexity is \(O(2\delta d)\) for the receiver and \(O(d+\delta ^\textsf{p})\) for the sender.
6 Fuzzy PSI in Low-Dimension Space
Clearly, with a fuzzy matching protocol in hand, we could straightforwardly execute a protocol instance for every pair of points from both the sender and receiver. Yet, this approach would lead to a quadratic increase in computational and communicative overheads. In the following sections, we depict some methods to circumvent this quadratic overhead, addressing both low-dimensional (in Sect. 6) and high-dimensional (in Sect. 7) spaces separately. We will deal with PSI-CA first (i.e., only let the receiver learn the cardinality of the intersection), then show how to extend PSI-CA to broader functionalities in Sect. 8, including standard PSI, labeled PSI, and circuit PSI.
6.1 Spatial Hashing Techniques
Consider the case that points are located in a low-dimension space \(\mathcal {U}^d\) (e.g., \(d=o(\log (\lambda )\)) where \(\mathcal {U}\) is the universe for each dimension. We use a similar idea from [20] to tile the entire space into hypercubes with side length \(2\delta \), but we consider a more general \(L_\textsf{p}\) distance setting. That is, we consider \(L_\textsf{p}\) distance over a space tiled by \(L_\infty \) hypercubes. We denote each hypercube as a cell. Specifically, given a point \(\textbf{w}\in \mathcal {U}^d\), the index \(\textsf{id}_i\) of each cell \(\mathcal {C}\) on each dimension \(i\in [d]\) is determined by \(\textsf{id}_i=\lfloor \frac{w_i}{2\delta }\rfloor \) and each cell is labeled by \(\textsf{id}_0\,\Vert \dots \Vert \,\textsf{id}_d\). The proofs of the following results are given in the full version of the paper [2].
Lemma 3
(Maximal Distance in a Cell). Given two points \(\textbf{w},\textbf{q}\in \mathcal {U}^d\) located in the same cell with side length \(2\delta \), then the distance between them is \(\textsf{dist}_\textsf{p}(\textbf{w},\textbf{q})<2\delta d^{\frac{1}{\textsf{p}}}\) where \(\textsf{p}\in [1,\infty ]\). Specifically, if \(\textsf{p}=\infty \), \(\textsf{dist}_\infty (\textbf{w},\textbf{q})<2\delta \).
Lemma 4
(Unique Center). Suppose there are multiple \(L_\textsf{p}\) balls (\(\textsf{p}\in [1,\infty ]\)) with radius \(\delta \) lying in a d-dimension space which is tiled by hypercubes (i.e., cells) with side length \(2\delta \). If these balls’ centers are at least \(2\delta d^{\frac{1}{\textsf{p}}}\) apart, then for each cell, there is at most one center of the balls lying in this cell. Specifically, if \(\textsf{p}=\infty \), then the unique center holds for disjoint balls since \(2\delta d^{\frac{1}{\textsf{p}}}\) degrades to \(2\delta \) in this case.
Lemma 5
(Unique Ball). Suppose there are multiple \(\delta \)-radius \(L_\textsf{p}\) balls (\(\textsf{p}\in [1,\infty ]\)) distributed in a \(d\)-dimension space which is tiled by hypercubes (cells) of side length \(2\delta \). If these balls’ centers are at least \(2\delta (d^{\frac{1}{\textsf{p}}}+1)\) apart from each other, then there exists at most one ball intersecting with the same cell. Specifically, if \(\textsf{p}=\infty \), this holds for \(L_\infty \) balls with \(4\delta \)-apart centers.
Lemma 6
(Unique Block). Any \(L_\infty \) ball with radius \(\delta \) will intersect with exactly \(2^d\) cells with side length \(2\delta \) in a d-dimension space. Moreover, if we denote such \(2^d\) cells together as a block (which is a hypercube with side length \(4\delta \)), then each block is unique for each disjoint ball. In other words, any two disjoint balls must be associated with different blocks.
6.2 Fuzzy PSI-CA for Infinity Distance
We provide the detailed protocol in Fig. 6 realizing fuzzy PSI-CA for infinity distance where the receiver’s points are \(2\delta \) apart from each other (i.e., the receiver’s \(\delta \)-radius balls are disjoint). In the figure, \(\textsf{block}_{4\delta }\) returns the label of the block of side-length \(4\delta \), \(\textsf{cell}_{2\delta }\) returns the label of the cell of side-length \(2\delta \), and \(\textsf{GetList},\textsf{GetTuple}\) are provided in Fig. 4. The proofs of the following theorems can be found in the full version of the paper [2], and we also generalize this approach to the setting where both parties hold a structured set of hyperballs.
Theorem 7
(Correctness). The protocol presented in Fig. 6 is correct with probability \(1-\textsf{negl}\!\!\left( \kappa \right) \) if \(\textsf{OKVS}\) satisfies perfect correctness defined in Sect. 3.1 and the independence property from Lemma 1, \(\textsf{H}_\gamma :\{0,1\}^*\mapsto \{0,1\}^\gamma ,\textsf{H}_{\kappa '}:\mathbb {G}\mapsto \{0,1\}^{\kappa '}\) used in \(\textsf{GetList},\textsf{GetTuple}\) are universal hash functions where \(\gamma =\kappa +\log (MN\delta )\), \(\kappa '=\kappa +d\log M\), and the receiver’s points are \(2\delta \) apart.
Theorem 8
(Security). The protocol presented in Fig. 6 realizes the fuzzy PSI-CA functionality defined in Fig. 2 for infinity distance against semi-honest adversaries if \(\textsf{OKVS}\) is oblivious, and the DDH assumption holds.
Theorem 9
(Complexity). The protocol provided in Fig. 6 has communication complexity \(O(2\delta dN\lambda +2^dM(\lambda +\kappa '))\) where \(\lambda ,\kappa =\kappa '-d\log M\) are the security and statistical parameters; The computational complexity is \(O(2\delta dN+2^d M)\) for the receiver and \(O(2^d dM)\) for the sender.
6.3 Fuzzy PSI-CA for Minkowski Distance
Assuming that the receiver’s points are spaced \(2\delta (d^{\frac{1}{\textsf{p}}}+1)\) apart, we can allow the receiver to iterate through each possible location, as depicted in Fig. 7. The proofs of the following theorems can be found in the full version of the paper [2]
Theorem 10
(Correctness). The protocol presented in Fig. 7 is correct with probability \(1-\textsf{negl}\!\!\left( \kappa \right) \) if \(\textsf{OKVS}\) satisfies the perfect correctness defined in Sect. 3.1 and the independence property from Lemma 1, \(\textsf{H}_\gamma :\{0,1\}^*\mapsto \{0,1\}^\gamma ,\textsf{H}_{\kappa '}:\mathbb {G}\mapsto \{0,1\}^{\kappa '}\) used in \(\textsf{GetList},\textsf{GetTuple}\) are universal hash functions where \(\gamma =\kappa +d\log (\delta N)+\log M\), \(\kappa '=\kappa +\textsf{p}\log (M\delta )\) if \(\textsf{p}<\infty \) and \(\kappa '=\kappa +\log M\) if \(\textsf{p}=\infty \), and the receiver’s points are \(2\delta (d^{\frac{1}{\textsf{p}}}+1)\) apart for \(\textsf{p}\in [1,\infty ]\).
Theorem 11
(Security). The protocol presented in Fig. 7 realizes the fuzzy PSI-CA functionality defined in Fig. 2 for \(L_{\textsf{p}\in [1,\infty ]}\) distance against semi-honest adversaries if \(\textsf{OKVS}\) is oblivious and the DDH assumption holds. Additionally, if \(\textsf{p}<\infty \), the hash function \(\textsf{H}_{\kappa '}:\mathbb {G}\mapsto \{0,1\}^{\kappa '}\) is modeled as a random oracle.
Theorem 12
(Complexity). The protocol provided in Fig. 7 has communication complexity \(O(2\delta d2^dN\lambda +M(\lambda +\kappa '))\) when \(L_\textsf{p}=L_\infty \) and \(O(2\delta d2^dN\lambda +M(2\lambda +\delta ^\textsf{p}\kappa '))\) when \(\textsf{p}\in [1,\infty )\) where \(\lambda ,\kappa \) are the security and statistical parameters. Specifically, \(\kappa =\kappa '-\log M\) if \(\textsf{p}=\infty \) and \(\kappa =\kappa '-\textsf{p}\log (M\delta )\) otherwise. The receiver’s computational complexity is \(O(2\delta d2^dN+M)\); The sender’s computational complexity is O(dM) if \(\textsf{p}=\infty \), and \(O(dM+\delta ^\textsf{p})\) otherwise.
7 Fuzzy PSI in High-Dimension Space
In this section, we construct an efficient fuzzy PSI protocol in a high-dimensional space, i.e., of a polynomially large dimension. For infinity distance, we provide a fuzzy PSI-CA protocol in Sect. 7.1 and extend it to richer functionalities in Sect. 8; For Minkowski distance, please refer to the full version of the paper [2] for details.
7.1 Infinity Distance
Suppose we assume the receiver’s set has good distribution in a high-dimensional space, particularly if each ball has disjoint projections (i.e., separated) from others on at least one dimension. In this case, we can get communication and computation complexity both scaling polynomially in the dimension. For instance, if balls are uniformly distributed, then it satisfies this predicate with overwhelming probability. The proof of this can be found in the full version of the paper [2].
Definition 2
(Separated Balls). The set of \(\delta \)-radius balls are separated in a \(d\)-dimension space if and only if the projections are separated on at least one dimension for each ball. Specifically, for the center \(\textbf{w}_{k}\) of each ball in the set, there exists some dimension \(i_*\in [d]\) such that
where \(\{w_{k',i_*}+j'\}\) is the set of projections from other balls.
Lemma 7
(Uniform Distribution). If centers of the balls are uniformly distributed (
 ) where \(\mathcal {U}:=\mathbb {Z}_{2^u}\), then it has the property defined in Definition 2 with probability \(1-\textsf{negl}\!\!\left( d\right) \).
) where \(\mathcal {U}:=\mathbb {Z}_{2^u}\), then it has the property defined in Definition 2 with probability \(1-\textsf{negl}\!\!\left( d\right) \).
Given the receiver’s balls are separated as defined in Definition 2, we provide an efficient protocol in Fig. 8 which gets rid of the \(2^d\) term for both communication and computation. The proofs of the following theorems can be found in the full version of the paper [2].
Theorem 13
(Correctness). The protocol presented in Fig. 8 is correct with probability \(1-\textsf{negl}\!\!\left( \kappa \right) \) if \(\textsf{OKVS}\) satisfies the perfect correctness, \(\mathbb {F}_p\)-linearity defined in Sect. 3.1 and the independence property from Lemma 1, \(\textsf{H}_\gamma :\{0,1\}^*\mapsto \{0,1\}^\gamma ,\textsf{H}_{\kappa '}:\mathbb {G}\mapsto \{0,1\}^{\kappa '}\) are universal hash functions where \(\gamma =\kappa +\log NM\delta \), \(\kappa '=\kappa +\log M\), and the receiver’s set are separated as defined in Definition 2. Particularly, we require that the decoding vector satisfies \(\textsf{dec}(\cdot )\in \{0,1\}^m\) and \(\textsf{HammingWeight}(\textsf{dec}(\cdot ))=O(\kappa )\) where \(m\) is the size of the \(\textsf{OKVS}\).
Theorem 14
(Security). The protocol presented in Fig. 8 satisfies the fuzzy PSI-CA functionality defined in Fig. 2 for infinity distance against semi-honest adversaries if \(\textsf{OKVS}\) is doubly oblivious, and the DDH assumption holds.
Theorem 15
(Complexity). The protocol presented in Fig. 8 has communication complexity \(O\left( (2\delta d)^2N\lambda +M(\lambda +\kappa )\right) \) where \(\lambda \), \(\kappa =\kappa '-\log M\) are computational and statistical parameters; The computational complexity is \(O((2\delta d)^2N+M)\) for the receiver and \(O(2d^2 M)\) for the sender.
8 Extending to Broader Functionalities
We show above protocols can be extended to a broader class of functionalities, including standard PSI, PSI with sender privacy, labeled PSI, and circuit PSI, with small tweaks and therefore preserving the efficiency. We describe extensions for all protocols in this work except for the \(L_\textsf{p}\) distance protocol in high dimensional space since currently, the simulator for a corrupt receiver needs to know the points of the sender that lie in the intersection, i.e., only works for the standard PSI functionality. We describe the main idea behind the extensions and give the formal details for the different protocol settings (including PSI with sender privacy and circuit PSI) in the full version of the paper [2].
Labeled PSI. For labeled PSI, the sender has some labels \(\textsf{label}_k\in \{0,1\}^{\sigma }\) attached to their input points \(\textbf{q}_k\), \(k\in [M]\), and the receiver wishes to learn the labels of the points for which there exists an \(i\in [N]\) such that \(\textsf{dist}(\textbf{w}_i,\textbf{q}_k)\le \delta \) (see Fig. 2 for the ideal functionality). It can be realized for the protocol in Fig. 6 (and similar for the protocols in Figs. 7 and 8 by ignoring the index j in these cases) by letting the sender use \(v_{k,j}\) as a one-time pad to encrypt \(\textsf{label}_k\) together with a special prefix, e.g., \(0^{\kappa }\), indicating that the label belongs to a valid match. For the protocol in Fig. 7 with \(\textsf{p}\ne \infty \), the sender instead uses the \(x_{k,j}\in \mathcal {X}_k\) as a one-time pad to encrypt \(0^{\kappa }\Vert \textsf{label}_k\).
Standard PSI. By letting the labels be a description of the sender’s points, we can realize standard PSI, where the receiver learns the sender’s points \(\textbf{q}_k\) for which there exists an \(i\in [N]\) such that \(\textsf{dist}(\textbf{w}_i,\textbf{q}_k)\le \delta \) (see Fig. 2 for the ideal functionality).
9 Performance Evaluation
In this section, we provide a micro-benchmark for our fuzzy PSI protocols for \(L_{\textsf{p}\in \{1,2,\infty \}}\) in low-dimension settings.
Implementation. We implement the standard fuzzy PSI variant (i.e., the receiver learns the sender’s points in the intersection) in three different metrics (\(L_\infty ,L_1,L_2\)) in a \(d\)-dimension space where \(d=\{2,3,5,10\}\), following the Figs. 6, and 7. The proof-of-concept implementationFootnote 5 is written in Rust, with less than \(1000\) lines of code. We use Risttreto and curve25519-dalek to instantiate the underlying group \(\mathbb {G}\), use FxHash and Blake3 to instantiate the hash function \(\textsf{H}_\gamma ,\textsf{H}_{\kappa '}\). We choose the security parameter \(\lambda =128\) and statistical parameter \(\kappa =40\) as usual. To instantiate the \(\textsf{OKVS}\), we follow the construction from [6] but working in \(\mathbb {F}_p\) and the expansion rate \(\epsilon =0.5\) to make sure we have \(2^{-\kappa }\) correctness error rate. Though it can be optimized to \(\epsilon =0.1\sim 0.25\) to have a more compact size, the encoding and decoding time would also increase accordingly.
Environment. We run the experiments on an ordinary laptop over a single thread: Macbook Air (M1 2020) with 8 GB RAM and a 2.1 GHz CPU, without using SIMD (e.g., AVX, NEON) optimizations. We measure the entire protocol time in a local network setting (i.e., LAN-like) without considering latency.
9.1 Concrete Performance
Fuzzy PSI. We mainly consider three cases for fuzzy PSI protocols: The receiver’s points are \(2\delta \)-apart (shown in Table 2), and \(2\delta (d^\frac{1}{\textsf{p}}+1)\)-apart (shown in Table 3). It is worth noting that, any distribution of the receiver’s points can be reduced to the disjoint setting by varying the radius. Specifically, for the \(L_\infty \) metric, the second case degrades to \(4\delta \)-apart points; For the \(L_{\{1,2\}}\) metric, our protocol only supports the second case. Our protocols can support large volume balls since our computation and communication cost scaled only sub-linearly to the total volume. In the full version of the paper [2] we also explore the setting where both receiver and sender hold a structured set consisting of hyperballs.
For comparison, we estimate the concrete communication cost for [20] based on their concrete bFSS size table reported in the paper. For the disjoint balls setting we use the reported share sizes for their spatial hash \(\circ \) sum \(\circ \) tensor \(\circ \) ggm (0.5, 1)-bFSS, assume bFSS evaluation to cost \((2\log {\delta })^d\) PRG calls, estimate PRG calls to take 10 machine cycles using AES-NI, and put \(\ell =440\). For the distance \(>4\delta \) setting we use the reported share sizes for their spatial hash \(\circ \) concat \(\circ \) tt \((1-1/2^d,d)\)-bFSS, assume bFSS evaluation to cost 1 machine cycle and put \(\ell =162\) for dimension \(d=5\), \(\ell =139\) for dimension \(d=10\). In all settings we estimate the correlation-robust hash calls at the end of the protocol to take around 10 machine cycles/byte, based on the fastest performance reported in [25] on 64-byte inputs. We assume a universe size of 32-bit integers for each dimension. Note that here we report the most conservative estimates for their running time and can only be considered as a loose lower bound.
10 Conclusion
In this work, we explored the fuzzy PSI in a more general setting, including higher dimensional space, comprehensive \(L_\textsf{p}\) distance metric, and extended functionality variants. We also demonstrate the practicality of our protocols by experimental results. However, there are still many open problems to be solved, such as, our \(L_\textsf{p}\) protocols have an additional \(O(\delta ^\textsf{p})\) communication overhead for each sender’s point which might be expensive when \(\delta \) or \(\textsf{p}\) is too large. Another interesting problem to think is how to get a more efficient protocol in polynomially large dimension space for \(L_2\) distance, or if we can weaken the separated assumption further for \(L_\infty \) distance? We leave them as well as the concrete efficiency optimization to future works. Also, current fuzzy PSI protocols with negligible correctness error require disjoint balls at least. What if the receiver’s balls are intersected? Any non-trivial approaches without quadratic overhead would be interesting to explore.
Notes
- 1.
The overhead of \(L_1\) balls would be \(\frac{2^d}{d}\) times larger than that of \(L_\infty \) balls in their protocols.
- 2.
Assuming the group order \(p\) is large enough that \(t^\textsf{p}< p\).
- 3.
Note that this is not a problem in their setting as they use the function secret sharing (FSS) to handle each grid cell.
- 4.
The neighborhood is a hypercube of side-length \(6\delta \).
- 5.
The open-sourced repository: https://github.com/sihangpu/fuzzy_PSI.
References
Alamati, N., Branco, P., Döttling, N., Garg, S., Hajiabadi, M., Pu, S.: Laconic private set intersection and applications. In: Nissim, K., Waters, B. (eds.) TCC 2021. LNCS, vol. 13044, pp. 94–125. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-90456-2_4
van Baarsen, A., Pu, S.: Fuzzy private set intersection with large hyperballs. Cryptology ePrint Archive, Paper 2024/330 (2024). https://eprint.iacr.org/2024/330
Badrinarayanan, S., Miao, P., Raghuraman, S., Rindal, P.: Multi-party threshold private set intersection with sublinear communication. In: Garay, J.A. (ed.) PKC 2021, Part II. LNCS, vol. 12711, pp. 349–379. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-75248-4_13
Bartusek, J., Garg, S., Jain, A., Policharla, G.V.: End-to-end secure messaging with traceability only for illegal content. In: Hazay, C., Stam, M. (eds.) Advances in Cryptology – EUROCRYPT 2023. LNCS, Part V, Germany, Lyon, France, 23–27 April 2023, vol. 14008, pp. 35–66. Springer, Heidelberg (2023). https://doi.org/10.1007/978-3-031-30589-4_2
Bhowmick, A., Boneh, D., Myers, S., Talwar, K., Tarbe, K.: The Apple PSI system (2021). https://www.apple.com/child-safety/pdf/Apple_PSI_System_Security_Protocol_and_Analysis.pdf
Bienstock, A., Patel, S., Seo, J.Y., Yeo, K.: Near-optimal oblivious key-value stores for efficient PSI, PSU and volume-hiding multi-maps. In: USENIX Security Symposium, pp. 301–318. USENIX Association (2023)
Branco, P., Döttling, N., Pu, S.: Multiparty cardinality testing for threshold private intersection. In: Garay, J. (ed.) 24th International Conference on Theory and Practice of Public Key Cryptography, PKC 2021. LNCS, Part II, Virtual Event, 10–13 May 2021, vol. 12711, pp. 32–60. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-030-75248-4_2
Chakraborti, A., Fanti, G., Reiter, M.K.: Distance-aware private set intersection. In: USENIX Security Symposium. USENIX Association (2023)
Chase, M., Miao, P.: Private set intersection in the internet setting from lightweight oblivious PRF. In: Micciancio, D., Ristenpart, T. (eds.) CRYPTO 2020, Part III. LNCS, vol. 12172, pp. 34–63. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-56877-1_2
Chen, H., Huang, Z., Laine, K., Rindal, P.: Labeled PSI from fully homomorphic encryption with malicious security. In: Lie, D., Mannan, M., Backes, M., Wang, X. (eds.) 25th Conference on Computer and Communications Security, ACM CCS 2018, Toronto, ON, Canada, 15–19 October 2018, pp. 1223–1237. ACM Press (2018). https://doi.org/10.1145/3243734.3243836
Chen, H., Laine, K., Rindal, P.: Fast private set intersection from homomorphic encryption. In: Thuraisingham, B.M., Evans, D., Malkin, T., Xu, D. (eds.) 24th Conference on Computer and Communications Security, ACM CCS 2017, Dallas, TX, USA, 31 October–November 2 2017, pp. 1243–1255. ACM Press (2017). https://doi.org/10.1145/3133956.3134061
Chmielewski, L., Hoepman, J.: Fuzzy private matching (extended abstract). In: ARES, pp. 327–334. IEEE Computer Society (2008)
Chor, B., Gilboa, N., Naor, M.: Private information retrieval by keywords. Cryptology ePrint Archive, Report 1998/003 (1998). https://eprint.iacr.org/1998/003
Cong, K., et al.: Labeled PSI from homomorphic encryption with reduced computation and communication. In: Vigna, G., Shi, E. (eds.) 28th Conference on Computer and Communications Security, ACM CCS 2021, Virtual Event, Republic of Korea, 15–19 November 2021, pp. 1135–1150. ACM Press (2021). https://doi.org/10.1145/3460120.3484760
Dong, C., Chen, L., Wen, Z.: When private set intersection meets big data: an efficient and scalable protocol. In: Sadeghi, A.R., Gligor, V.D., Yung, M. (eds.) 20th Conference on Computer and Communications Security, ACM CCS 2013, Berlin, Germany, 4–8 November 2013, pp. 789–800. ACM Press (2013). https://doi.org/10.1145/2508859.2516701
Duong, T., Phan, D.H., Trieu, N.: Catalic: delegated PSI cardinality with applications to contact tracing. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020, Part III. LNCS, vol. 12493, pp. 870–899. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64840-4_29
Dupont, P.-A., Hesse, J., Pointcheval, D., Reyzin, L., Yakoubov, S.: Fuzzy password-authenticated key exchange. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10822, pp. 393–424. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_13
Freedman, M.J., Nissim, K., Pinkas, B.: Efficient private matching and set intersection. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 1–19. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_1
Garimella, G., Pinkas, B., Rosulek, M., Trieu, N., Yanai, A.: Oblivious key-value stores and amplification for private set intersection. In: Malkin, T., Peikert, C. (eds.) CRYPTO 2021, Part II. LNCS, vol. 12826, pp. 395–425. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84245-1_14
Garimella, G., Rosulek, M., Singh, J.: Structure-aware private set intersection, with applications to fuzzy matching. In: Dodis, Y., Shrimpton, T. (eds.) Advances in Cryptology, CRYPTO 2022, Part I. LNCS, Santa Barbara, CA, USA, 15–18 August 2022, vol. 13507, pp. 323–352. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-15802-5_12
Garimella, G., Rosulek, M., Singh, J.: Malicious secure, structure-aware private set intersection. In: Handschuh, H., Lysyanskaya, A. (eds.) Advances in Cryptology, CRYPTO 2023, Part I. LNCS, Santa Barbara, CA, USA, 20–24 August 2023, vol. 14081, pp. 577–610. Springer, Heidelberg (2023). https://doi.org/10.1007/978-3-031-38557-5_19
Ghosh, S., Simkin, M.: The communication complexity of threshold private set intersection. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11693, pp. 3–29. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_1
Ghosh, S., Simkin, M.: Threshold private set intersection with better communication complexity. In: Boldyreva, A., Kolesnikov, V. (eds.) 26th International Conference on Theory and Practice of Public Key Cryptography, PKC 2023, Part II. LNCS, Atlanta, GA, USA, 7–10 May 2023, vol. 13941, pp. 251–272. Springer, Heidelberg (2023). https://doi.org/10.1007/978-3-031-31371-4_9
Huang, Y., Evans, D., Katz, J.: Private set intersection: are garbled circuits better than custom protocols? In: ISOC Network and Distributed System Security Symposium, NDSS 2012, San Diego, CA, USA, 5–8 February 2012. The Internet Society (2012)
ECRYPT II: eBACS: ECRYPT Benchmarking of Cryptographic Systems (2023). https://bench.cr.yp.to/results-sha3
Indyk, P., Woodruff, D.P.: Polylogarithmic private approximations and efficient matching. In: Halevi, S., Rabin, T. (eds.) 3rd Theory of Cryptography Conference, TCC 2006. LNCS, New York, NY, USA, 4–7 March 2006, vol. 3876, pp. 245–264. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_13
Ion, M., et al.: On deploying secure computing: private intersection-sum-with-cardinality. In: EuroS &P, pp. 370–389. IEEE (2020)
Kolesnikov, V., Kumaresan, R., Rosulek, M., Trieu, N.: Efficient batched oblivious PRF with applications to private set intersection. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S. (eds.) 23rd Conference on Computer and Communications Security, ACM CCS 2016, Vienna, Austria, 24–28 October 2016, pp. 818–829. ACM Press (2016). https://doi.org/10.1145/2976749.2978381
Lindell, Y.: How to simulate it - a tutorial on the simulation proof technique. Cryptology ePrint Archive, Report 2016/046 (2016). https://eprint.iacr.org/2016/046
Meadows, C.: A more efficient cryptographic matchmaking protocol for use in the absence of a continuously available third party. In: S &P, pp. 134–137. IEEE Computer Society (1986)
Muffett, A.: Facebook: password hashing & authentication (2015). https://rwc.iacr.org/2015/program.html
Naor, M., Reingold, O.: Number-theoretic constructions of efficient pseudo-random functions. In: 38th Annual Symposium on Foundations of Computer Science, Miami Beach, Florida, 19–22 October 1997, pp. 458–467. IEEE Computer Society Press (1997). https://doi.org/10.1109/SFCS.1997.646134
Pal, B., et al.: Might I Get Pwned: a second generation compromised credential checking service. In: USENIX Security Symposium, pp. 1831–1848. USENIX Association (2022)
Pinkas, B., Schneider, T., Tkachenko, O., Yanai, A.: Efficient circuit-based PSI with linear communication. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11478, pp. 122–153. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_5
Raghuraman, S., Rindal, P.: Blazing fast PSI from improved OKVS and subfield VOLE. In: Yin, H., Stavrou, A., Cremers, C., Shi, E. (eds.) 29th Conference on Computer and Communications Security, ACM CCS 2022, Los Angeles, CA, USA, 7–11 November 2022, pp. 2505–2517. ACM Press (2022). https://doi.org/10.1145/3548606.3560658
Rindal, P., Schoppmann, P.: VOLE-PSI: fast OPRF and circuit-PSI from vector-OLE. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021, Part II. LNCS, vol. 12697, pp. 901–930. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77886-6_31
Uzun, E., Chung, S.P., Kolesnikov, V., Boldyreva, A., Lee, W.: Fuzzy labeled private set intersection with applications to private real-time biometric search. In: Bailey, M., Greenstadt, R. (eds.) 30th USENIX Security Symposium, USENIX Security 2021, 11–13 August 2021, pp. 911–928. USENIX Association (2021)
Ye, Q., Steinfeld, R., Pieprzyk, J., Wang, H.: Efficient fuzzy matching and intersection on private datasets. In: Lee, D., Hong, S. (eds.) ICISC 2009. LNCS, vol. 5984, pp. 211–228. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14423-3_15
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2024 International Association for Cryptologic Research
About this paper
Cite this paper
van Baarsen, A., Pu, S. (2024). Fuzzy Private Set Intersection with Large Hyperballs. In: Joye, M., Leander, G. (eds) Advances in Cryptology – EUROCRYPT 2024. EUROCRYPT 2024. Lecture Notes in Computer Science, vol 14655. Springer, Cham. https://doi.org/10.1007/978-3-031-58740-5_12
Download citation
DOI: https://doi.org/10.1007/978-3-031-58740-5_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-58739-9
Online ISBN: 978-3-031-58740-5
eBook Packages: Computer ScienceComputer Science (R0)


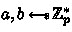 , to the receiver;
, to the receiver;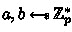 ;
;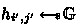 ;
;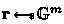 and
and 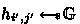 and
and  .
.
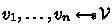 :
:  , there is
, there is 







