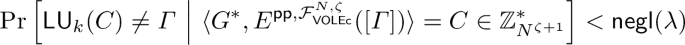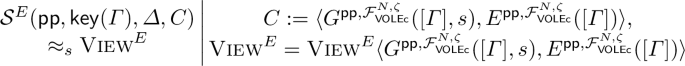Toward Malicious Constant-Rate 2PC via Arithmetic Garbling

Abstract

A recent work by Ball, Li, Lin, and Liu [Eurocrypt’23] presented a new instantiation of the arithmetic garbling paradigm introduced by Applebaum, Ishai, and Kushilevitz [FOCS’11]. In particular, Ball et al.’s garbling scheme is the first constant-rate garbled circuit over large enough bounded integer computations, inferring the first constant-round constant-rate secure two-party computation (2PC) over bounded integer computations in the presence of semi-honest adversaries.

The main source of difficulty in lifting the security of garbling schemes-based protocols to the malicious setting lies in proving the correctness of the underlying garbling scheme. In this work, we analyze the security of Ball et al.’s scheme in the presence of malicious attacks.

• We demonstrate an overflow attack, which is inevitable in this computational model, even if the garbled circuit is fully correct. Our attack follows by defining an adversary, corrupting either the garbler or the evaluator, that chooses a bad input and causes the computation to overflow, thus leaking information about the honest party’s input. By utilizing overflow attacks, we show that 1-bit leakage is necessary for achieving security against a malicious garbler, discarding the possibility of achieving full malicious security in this model. We further demonstrate a wider range of overflow attacks against a malicious evaluator with more than 1 bit of leakage.

• We boost the security level of Ball et al.’s scheme by utilizing two variants of Vector Oblivious Linear Evaluation, denoted by VOLEc and aVOLE. We present the first constant-round constant-rate 2PC protocol over bounded integer computations, in the presence of a malicious garbler with 1-bit leakage and a semi-honest evaluator, in the {VOLEc,aVOLE}-hybrid model and being black-box in the underlying group and ring. Compared to the semi-honest variant, our protocol incurs only a constant factor overhead, both in computation and communication. The constant-round and constant-rate properties hold even in the plain model.

1 Introduction

Secure two-party computation (2PC) [41] allows two mutually untrusting parties to jointly compute arbitrary public functions with their private inputs while only revealing the output. It has been deployed in many real-world use cases, including medicine, privacy-preserving machine learning, and many more.

While 2PC can be built based on multiple approaches, instantiating it using garbled circuits is one of the most popular methods due to its simplicity, flexibility, and high practicality in constant-round 2PC. In these protocols, a garbler (denoted by G) generates an encoded version of the publicly agreed circuit $\mathcal {C}$, referred to as a garbled circuit (GC). G further generates a set of garbled labels encoding all potential wire values of every input wire. Next, an evaluator (denoted by E) can evaluate the GC on a single input to get the corresponding output upon obtaining the GC and the garbled input labels.

A garbled circuit is a cryptographic object consisting of three algorithms: (1) circuit encoding, (2) input encoding, and (3) evaluation, where security is followed by privacy and correctness. Namely, privacy implies that the former two encoding algorithms can be simulated without accessing the input to the computation x, whereas correctness ensures that the evaluator learns $\mathcal {C} (x)$. Garbled circuits easily imply passive (semi-honest) 2PC, given that the parties have access to parallel semi-honest oblivious-transfer [30] or oblivious linear evaluation, where the communication rate is ${\mathcal {O}}(\kappa )$ for a security parameter $\kappa$.¹

Yao’s Boolean GC. The classic approach for designing garbled circuits, commonly known as Yao’s GC, considers garbling Boolean circuits consisting of AND and XOR gates. It was first introduced by Yao in 1986 [41] and later refined in [30] as a scheme requiring $4\kappa$ bits of communication per gate. Following these, a long line of work has devoted substantial effort to improving the communication overhead. Notable improvements include row reduction (GRR3) [33], which reduced the communication per gate to $3\kappa$; free XOR [27], which eliminated the communication for XOR gates; half-gates [42], which reduced the communication per AND gate to $2\kappa$ while being compatible with free XOR; and most recently, the three halves [37], which achieves state of the art $1.5\kappa$ bits per AND gate. This great effort did not improve the asymptotic communication rate for arbitrary circuits. Namely, the communication rate remained ${\mathcal {O}}(\kappa )$.

Arithmetic GC over Bounded Integer Computations. To break the barrier of ${\mathcal {O}}(\kappa )$ rate, a natural attempt is to design garbling schemes for computations defined beyond Boolean circuits, e.g., a circuit defined over some ring $\mathcal {R}$. One such endeavor led by Ball et al. [4] to generalize free XOR to the bounded integer computations. The model of computation considers circuits defined over the integer ring $\mathbb {Z}$ with addition and multiplication gates and a pre-defined bound B, where any wire value falls within $[-B,B]$. Nevertheless, this effort did not achieve any asymptotic rate improvement due to employing bit decomposition techniques. Other attempts (e.g. [1, 25]) studied new approaches for arithmetic GC. However, their scope was limited to arithmetic formulas and branching programs. The first construction for arbitrary arithmetic circuits over bounded integer computations, which took a different route from Yao’s paradigm, was proposed by Applebaum, Ishai, and Kushilevitz (AIK) [2]. Their construction is based on the Learning With Errors (LWE) assumption while still requiring ${\mathcal {O}}(\kappa )$ rate. This rate is due to a so-called key extension (KE) gadget that enables E to expand a short garbled label to a long one while encoding the same value. At the core of this construction lies a key and message homomorphic encryption scheme, and AIK illustrated how to instantiate this encryption scheme with LWE. Building on [2], a recent work by Ball et al. [3] improved over the AIK paradigm by introducing an alternative instantiation of their KE gadget based on the Decisional Composite Residuosity (DCR) assumption over Paillier groups [13, 35]. Notably, [3]’s GC over B-bounded integer computations achieves ${\mathcal {O}}(1)$ rate for a large enough bound $B=B(\lambda )$. This implies the first semi-honest constant-round constant-rate 2PC protocol in this computational model. Henceforth, we use the term BLLL’s GC to denote the constant-rate GC scheme in [3]. We note that [3] additionally proposed GC schemes for other models, but only the GC for bounded integer computations achieves a constant rate.

Active 2PC via Yao’s GC. Lifting the security of the Yao semi-honest protocols to the active (aka, malicious) setting is challenging due to the intricate task of proving the correctness of a garbled circuit. In theory, boosting passive to active is feasible with a constant communication overhead due to the GMW compiler [19] and succinct proofs. Nevertheless, its high computation cost keeps encouraging researchers to develop more desirable solutions. Many of these works, explicitly or implicitly, exploit the fact that Yao’s GC is naturally secure against a malicious E. Namely, the main focus becomes forcing a malicious G to provide a correct GC. Within the developed methods, the cut-and-choose paradigm [23, 28, 29] addresses some of the practicality concerns by repeating the garbling procedure multiple times but inflates the overheads by a factor of statistical parameter $\lambda$ to achieve $2^{-\lambda }$ error. A different approach applies authentication to the wire labels [12, 14, 20, 24, 39], while achieving constant communication overhead.

With the aim of reducing the concrete communication overhead, another line of work weakens the standard security notion, allowing the adversary to learn one bit of information about the honest party’s input. This notion is denoted by security with 1-bit leakage. Several variants of this notion have been considered in the literature, such as the dual execution paradigm [22, 26, 32, 36] and one-sided leakage [20]. This security relaxation enables constant communication factor overheads where the concrete factors are smaller than 2.

1.1 Our Contributions

Motivated by the recent breakthrough achieved by BLLL’s GC, we focus on constructing constant-rate constant-round 2PC over bounded integer computations in the presence of static malicious adversaries. Our focus is not only feasibility but also practicality. We list our following contributions:

• Observing a security subtlety in the bounded computational model. We discuss an issue in the bounded integer computation model, which is inherited by the nature of the computation. Namely, a B-bounded input may still cause an internal wire value to overflow. Nevertheless, the model does not specify what should be the output in case of an inadmissible input, partly because a party cannot tell whether an input is admissible without viewing the other party’s input. While this is not required in the semi-honest setting, it eliminates the possibility of obtaining full security in the active setting, as an adversary may choose its input maliciously. We stress that this issue holds even if the attack is limited to only modifying the input to the computation.

• Understanding the active security of BLLL garbling. We demonstrate a new class of attacks coined overflow attacks and show that these attacks are inevitable in BLLL’s GC because even with a fully correct GC, both G and E can exploit this attack to compromise the privacy of the honest party’s inputs. This attack implies that the best notion of security in the bounded integer model via BLLL’s GC in the presence of a malicious G and a semi-honest E is security with 1-bit leakage, as the leakage boils down to whether E aborted or not. We further show that this is not necessarily the case in the presence of a malicious E, which may leak the entire input of G by demonstrating a larger class of attacks overflowing multiple wires.

• Lifting BLLL’s GC to the active setting. We construct a practical 2PC protocol over bounded integer computations, achieving the above best notion of security using two hybrids (see Theorem 1). The first hybrid refers to Vector Oblivious Linear Evaluation correlations² (VOLEc) functionality [10, 11, 31] that can be instantiated based on the LPN assumption with sublinear communication cost, whereas the second hybrid refers to the so-called authenticated VOLE³ (aVOLE) functionality that our protocol uses to allow the evaluator to learn his garbled input labels. We do not instantiate the aVOLE functionality since its effect on the overall cost vanishes with the circuit’s size as its complexity grows with E’s input size. Therefore, even general malicious 2PC can be used here. Overall, our protocol is constant-round and maintains both constant computation and communication multiplicative overheads compared to the semi-honest variant in the {VOLEc, aVOLE}-hybrid model, where the VOLE correlations can be generated in a circuit-independent pre-processing phase. Moreover, our protocol achieves a constant communication rate even in the plain model and only uses black-box access to the underlying group and ring. To construct our protocol, we transfer the VOLE-based ZK (e.g., [15]) to the integer ring $\mathbb {Z}_{N^\zeta }$ where N is an RSA modulus and $\zeta \in \mathbb {Z}^+$, as well as design a customized $\varSigma$-protocol [38], which could have independent interests.

Theorem 1

(Informal, Main). Assuming DCR assumption over $\mathbb {Z}^*_{N^{\zeta +1}}$ where $N=pq$ is a safe RSA modulus and $\zeta$ is a sufficiently large integer. There exists a constant-rate constant-round secure two-party computation protocol for any circuit $\mathcal {C}$ over B-bounded integer computations in the {VOLEc, aVOLE}-hybrid model instantiated via BLLL’s GC [3], where the computation is linear in $|\mathcal {C} |$. The protocol is secure against malicious G with 1-bit leakage and semi-honest E.

1.2 Technical Overview

In this section, we informally explain our techniques while neglecting less important details; we refer to Sect. 3 for a complete overview of BLLL’s GC.

Overflow Attacks. We begin with an overview of the subtlety within the bounded integer computation model. While considering active adversaries, we noticed that B-bounded inputs do not guarantee that all wires will be B-bounded, where an intermediate wire can overflow. Such an overflow may occur even if the garbled circuit is constructed correctly and, in the presence of corrupting, either G or E. I.e., the adversary can set B-bounded inputs but try to cause the evaluation of GC to suffer from overflows on intermediate wires. We call these inputs legal but inadmissible. Now, since the evaluation procedure of BLLL’s GC heavily relies on all wires being B-bounded, overflow attacks can help a malicious E to break the privacy guarantee of BLLL’s GC scheme and a malicious G to cause an input-dependent select-failure abort as follows:

• Malicious E (see Sect. 4.1): While evaluating a BLLL’s GC, E obtains a garbled label encoding a private value on each wire. There are ${\mathcal {O}}(|\mathcal {C} |)$ wires in the BLLL’s GC having the following property: if the wire encoding a value w, the garbled label during evaluation will reveal $w+r$ to E where r is uniformly chosen from a larger fixed bound $B_{\textsf{e}}$ such that $w+r$ statistically hides w. Note that $w+r$ can only be leaked to E if w is bounded by B. When E uses bad inputs and w overflows, $w+r$ no longer hides w, so it should not be leaked to E. Essentially, E can select his inputs and monitor whether each wire overflows to make G’s inputs leak.

• Malicious G (see Sect. 4.2): While evaluating a BLLL’s GC, E needs to decode ${\mathcal {O}}(|\mathcal {C} |)$ garbled labels from domain $\mathbb {Z}_{N^\zeta }$ to $\mathbb {Z}$.⁴ In particular, E can decode these labels because they are B-bounded, so they will not wrap around the domain $\mathbb {Z}_{N^\zeta }$. When G uses bad inputs, the value could wrap around if some wire overflows. Hence, E might incorrectly decode the garbled labels and fail to evaluate the garbled tables, which will abort the execution. Thus, G can cause a selective failure attack, learning whether an overflow occurs, which can be captured as applying a predicate on E’s inputs.

Fig. 1.

The VOLE correlation functionality

VOLE Correlations and Authenticated VOLE over $\mathbb {Z}_{N^\zeta }$ as Hybrid Functionalities. Vector Oblivious Linear Evaluation (VOLE) allows a receiver (E in our protocol) to learn a linear combination of two vectors held by a sender (G in our protocol). In the case where the sender’s vectors and the receiver’s evaluation point are (pseudo-)random, known as VOLE correlation (VOLEc)⁵, recent works (e.g., [10]) show that it can be instantiated via the Learning Parity with Noise (LPN) assumption with sublinear communication cost, known as the Pseudorandom Correlation Generator (PCG) paradigm. Our 2PC protocol relies on “authenticating” G’s randomness in BLLL’s GC using VOLE correlations. In particular, we need to use VOLE correlations defined over $\mathbb {Z}_{N^\zeta }$ where N is an RSA modulus and $\zeta \in \mathbb {Z}^+$. Recently, Liu et al. [31] showed that the decisional LPN problem over the integer ring $\mathbb {Z}_{N^\zeta }$ is as hard as the LPN problems over the fields $\mathbb {F}_p$ and $\mathbb {F}_q$. Therefore, it is sufficient to generate VOLE correlations over $\mathbb {Z}_{N^\zeta }$ via the standard PCG paradigm to achieve sublinear cost in communication. Formally, this functionality is defined in Fig. 1.

Our protocol also uses another hybrid functionality called authenticated VOLE (aVOLE) to allow E to learn his input garbled labels (as the OT in Yao). The authenticated VOLE is just a small modification over the standard (non-randomized) VOLE where G holds 4 vectors $\boldsymbol{a},\boldsymbol{b},\boldsymbol{c},\boldsymbol{d}$ and E holds two elements $x, \varDelta$ such that E can learn $\boldsymbol{a}x+\boldsymbol{b}, \boldsymbol{a}\varDelta +\boldsymbol{c}, \boldsymbol{b}\varDelta +\boldsymbol{d}$. Crucially, the cost of instantiating this functionality is only proportional to E’s input size, so we do not instantiate it. See Fig. 4 and Sect. 5.3 for more discussions.

Our Protocol. Overflow attacks imply that the best we can hope while boosting the security of BLLL’s GC is 1-bit leakage security in the presence of malicious G and a semi-honest E. We notice that to achieve this security notion, we only need to guarantee that E must obtain a result of the intended computation whenever it evaluates the circuit and does not abort. This means that a malicious G can either learn the output of $\mathcal {C}$ or that E had aborted.

Interestingly, we observe that this can be guaranteed by an almost correct rather than fully correct BLLL’s GC (see Sect. 4.2). By simplifying the statements, we can design custom zero-knowledge proofs (ZKP) at a very low cost. To see how it works, recall that the BLLL garbling procedure includes the following operations: (1) sample uniform randomness in $\mathbb {Z}_{N^\zeta }$; (2) add two random samples over $\mathbb {Z}_{N^\zeta }$; (3) multiply two random samples over $\mathbb {Z}_{N^\zeta }$; and (4) use two random samples a, b to construct an element in the group $\mathbb {Z}^*_{N^{\zeta +1}}$ as $\tau ^a(N+1)^b$ where $\tau$ is a public uniform $2N^\zeta$-th residue. The operation (4) generates the garbled tables for the KE gadgets. BLLL’s GC utilizes the homomorphism of this ciphertext format where $(\tau ^{a_1}(N+1)^{b_1})^k(\tau ^{a_2}(N+1)^{b_2})=\tau ^{a_1k+b_1}(N+1)^{a_2k+b_2}$. By obtaining $k, a_1k+b_1$ from the GC evaluation, E can obtain $a_2k+b_2$ by solving the discrete logarithm of $(N+1)^{a_2k+b_2}$ to the base $N+1$, which is known to be easy and commonly used in the Paillier cryptosystem [13, 35].

Inspired by the authenticated garbling method of [39], we observe that the randomness used in the garbling procedure of BLLL’s GC can be generated in an authenticated manner by VOLE correlations over $\mathbb {Z}_{N^\zeta }$ in a circuit-independent pre-processing phase. Namely, the ideal functionality $\mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }$ can be used to generate a pool of committed randomness over $\mathbb {Z}_{N^\zeta }$, which can replace operation (1). Later, during the GC generation procedure, G and E consume the committed randomness to authenticate the garbled circuit. I.e., G will use the committed randomness to produce correlated (and new committed) randomness for operations (2–3), and use special-purpose ZK proofs to validate that the computation of (4) is done almost correctly. In slightly more detail:

• To support operations (2–3): We transform the existing VOLE-based ZK proofs to the ring $\mathbb {Z}_{N^\zeta }$ domain (see Sect. 5.1), used to prove the correctness of addition/multiplication operations. The proof of each operation requires sending only ${\mathcal {O}}(1)$ elements and performing ${\mathcal {O}}(1)$ ring operations.

• To support operation (4): We observe that as long as a committed random element $b\in \mathbb {Z}_{N^\zeta }$ is indeed used to generate a garbled table ciphertext $\tau ^a(N+1)^b \in \mathbb {Z}^*_{N^{\zeta +1}}$ of some KE gadget, it ensures that E will perform an intended computation of the KE gadget upon evaluating it. Namely, an erroneous garbled table of form $\varepsilon (N+1)^b$ is harmless under 1-bit leakage where $\varepsilon$ can be an arbitrary error that is not dividable by $N+1$ in $\mathbb {Z}^*_{N^{\zeta +1}}$. By exploiting the order of $N+1$ in the group $\mathbb {Z}^*_{N^{\zeta +1}}$ is exactly $N^\zeta$, we adjust the well-known Schnorr’s $\varSigma$-protocol [38] for the knowledge of the discrete logarithm to achieve this (see Sect. 5.2). Roughly speaking, the crucial adjustment requires G to open the committed randomness in the response phase of $\varSigma$-protocol. The adjusted $\varSigma$-protocol is also very cheap and requires sending only ${\mathcal {O}}(1)$ group elements, and performing ${\mathcal {O}}(1)$ exponentiation in $\mathbb {Z}^*_{N^{\zeta +1}}$ (and ${\mathcal {O}}(1)$ additions/multiplications in $\mathbb {Z}_{N^{\zeta }}$).

To conclude, our protocol is constant-round⁶ and constant-rate, with constant factor blowup in both computation and communication (compared to [3]) in the $\{\mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }, \mathcal {F}_{\textsf{aVOLE}}^{N, \zeta }\}$-hybrid model, and only uses black-box access to the underlying group $\mathbb {Z}_{N^{\zeta }}$ and ring $\mathbb {Z}^*_{N^{\zeta +1}}$. The cost of our protocol is dominated by a total number of ${\mathcal {O}}(|\mathcal {C} |)$ operations (4), achieving constant factor blowup. Finally, by using LPN assumption over $\mathbb {Z}_{N^\zeta }$ to instantiate $\mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }$ with sublinear communication cost in ${\mathcal {O}}(|\mathcal {C} |)$, our protocol preserves a constant rate of communication, and constant-round, even in the plain model.

Full Version. Full version of this paper is available at [21].

2 Notations and Definitions

Our work uses the following notations:

• $\lambda$ is the statistical security parameter (e.g., 40).

• $\kappa$ is the computational security parameter (e.g., 128).

• $x \triangleq y$ denotes that x is defined as y. $x := y$ denotes that y is assigned to x.

• We denote that x is uniformly drawn from a set S by $x \overset{\$}{\leftarrow }S$.

• We denote $\{1,\ldots ,n\}$ by [n], $\{a, \ldots , b\}$ by [a, b].

• We denote vectors by bold lower-case letters (e.g., $\boldsymbol{a}$), where $a_i$ (or a[i]) denotes the ith component of $\boldsymbol{a}$ (starting from 1).

• We denote sets by bold upper-case letters (e.g., $\boldsymbol{A}$). In some cases, the elements in the set will be indexed via integer tuples (e.g., $A_{i,j,k}$).

• N denotes a safe RSA modulus. That is, $N=pq$ where p, q are equal-length large primes (e.g., 1024-bits). Moreover $p=2p'+1$ and $q=2q'+1$ where $p',q'$ are also primes. W.l.o.g., we assume $p<q$. Formally, p, q are sampled according to the security parameter $\lambda$.

• $\approx _{c}$ denotes the computational indistinguishability. $\approx _{s}$ denotes the statistical indistinguishability; see [18] for more details.

Due to space limitations, we defer the following definitions to our full version:

• We extend the classic security definition of 2PC and define secure two-party computation with 1-bit leakage in the Ideal/Real simulation paradigm, which is adopted from [20]. The main modification allows the adversary to submit a predicate to the ideal functionality.

• We include the DCR and LPN hardness assumptions. We include the hardness lemma regarding the LPN over $\mathbb {Z}_{N^\zeta }$, which is adopted from [31].

• We include the definitions for arithmetic garbling scheme over bounded integer computations and communication rate, adopted from [3].

3 A Review of Constant-Rate BLLL’s GC

Given that BLLL’s GC, building on AIK, dramatically deviates from the standard Yao’s paradigm, we provide a concise overview of this scheme in this section. Recall that the bounded integer computation model requires that, for a class of admissible inputs over $\mathbb {Z}$, all wire values fall within the range $[-B, B]$ for some predefined positive integer B. Naturally, the computation can be embedded into a large enough modular integer ring.

Fig. 2.

Information-theoretic add/mult gadgets from the AIK paradigm [2]

The AIK Paradigm for Arithmetic Garbling. BLLL’s GC follows the AIK paradigm [2] for arithmetic garbing. Unlike Yao’s GC, the AIK paradigm generates the GC backward, i.e., in the reverse topology order. To garble a circuit $\mathcal {C}$ defined over some integer ring $\mathcal {R}$ (i.e., the computation is defined over the integer ring $\mathcal {R}$), the AIK paradigm generates GC from the following components:

• Affine garbled labels: The AIK GC encodes garbled labels using affine functions. That is, for each wire w in $\mathcal {C}$, G assigns it with a pair of keys $(\boldsymbol{k}^w_0, \boldsymbol{k}^w_1) \in \mathcal {R}^{n}\times \mathcal {R}^{n}$ for some positive integer n. During the evaluation, E obtains a garbled label encoding w defined by $\boldsymbol{L}^w \triangleq \boldsymbol{k}^w_0 w + \boldsymbol{k}^w_1$. The key pair $(\boldsymbol{k}^w_0, \boldsymbol{k}^w_1)$ is denoted by the garbled key pair⁷ for wire w. In particular, $n=|\boldsymbol{k}^w_0|=|\boldsymbol{k}^w_0|$ denotes the length of the garbled key pair.

• Information-theoretic addition/multiplication gadgets: For a gate with input wires x, y and output wire z, E holding $\boldsymbol{L}^x$ and $\boldsymbol{L}^y$ should learn $\boldsymbol{L}^z$. The AIK GC achieves this in an information-theoretic way without communication. Essentially, G selects the garbled key pairs of two input wires after the garbled key pair of the output wire is assigned. The complete scheme is presented in Fig. 2. Note that the gate can have unlimited fan-out. Hence, the garbled key pair of wire z is constructed as the concatenation of all garbled key pairs of the wire z provided as inputs to the next layer.

• Key extension gadgets: While the constructions for addition/multiplication gadgets are information-theoretic, the length of the garbled key pairs grows exponentially backward because (1) the length for one garbled key pair of the inputs of a multiplication gate doubles and (2) a gate (including an input gate) can have unlimited fan-out. Thus, transferring garbled labels of inputs of $\mathcal {C}$ from G to E will require exponential costs. To tackle this issue, the AIK GC scheme introduced a garbled gadget called the key extension (KE) gadget. A KE gadget allows E to expand a short, so-called “version-A”, gabled label $\boldsymbol{L}^{w,A} \in \mathcal {R}^{n_s}$ to a longer “version-B” garbled label $\boldsymbol{L}^{w,B} \in \mathcal {R}^{n_l}$ (where $n_l>n_s$ and $n_s$ is a small constant), while encoding an identical value w. In other words, it can be viewed as augmenting $\mathcal {C}$ with extra “identical” gates. Recursively applying the KE gadgets will result in a KE gadget that allows E to expand a length n garbled label into any length. We emphasize that, since G garbles the circuit backward, a KE gadget helps G to shrink the length of the garbled key pair. That is, the length of the garbled key pair will no longer grow exponentially. Unlike the addition and multiplication gadgets, a KE gadget requires garbled tables to be transferred from G to E. [2] showed how to build KE gadgets from the Learning With Errors (LWE) assumption. Building on [2, 3] further showed how to build them based on the DCR assumption. Essentially, optimizing the communication cost requires building improved KE gadgets.

The complete garbling procedure of the AIK paradigm can be roughly viewed as follows: G assigns the output wires with garbled key pair (1, 0).⁸ G assigns the corresponding garbled key pair to each gate backward in a gate-by-gate manner. For the output wire of each gate (including an input gate), G applies a KE gadget to shrink the length of the garbled key pair to a value smaller than (or equal to) $n_s$. Finally, G obtains garbled key pairs for the input wires of input gates, each of a maximum length of $n_s$, where $n_s$ is a small constant. Then E can evaluate the circuit by obtaining the garbled labels of the inputs and the truth tables generated by the KE gadgets.

A General Paradigm to Construct KE. Both [2] and [3] utilize an encryption scheme with linear homomorphism to implement the KE gadget. Consider an integer ring $\mathcal {R}$ and an encryption scheme with the procedures $\textsf{enc}$ and $\textsf{dec}$, where $\textsf{enc}$ takes a key $k \in \mathcal {R}$ and a vector of messages $\boldsymbol{m}\in \mathcal {R}^n$ ($n > 2$) as its input and outputs a ciphertext denoted by $\textsf{enc}(k, \boldsymbol{m})$. The encryption scheme supports linear evaluation over keys and plaintexts. Namely, given a constant element $\beta \in \mathcal {R}$, a ciphertext $\textsf{enc}(k_1, \boldsymbol{m_1})$ that encrypts $\boldsymbol{m_1}$ under the key $k_1$ and a ciphertext $\textsf{enc}(k_2, \boldsymbol{m_2})$ that encrypts $\boldsymbol{m_2}$ under the key $k_2$, one can compute a ciphertext $\textsf{enc}(k_1\beta +k_2,\boldsymbol{m}_1\beta +\boldsymbol{m}_2)$ by computing where $\beta$ is embedded inside the ciphertext space and are operations defined over the ciphertext space. Recall that our goal is to let E with $\boldsymbol{L}^{w,A} \triangleq \boldsymbol{a} w + \boldsymbol{b}$ obtain $\boldsymbol{L}^{w,B} \triangleq \boldsymbol{c} w + \boldsymbol{d}$ where $\left( \boldsymbol{a},\boldsymbol{b}\right)$ and $\left( \boldsymbol{c},\boldsymbol{d}\right)$ are garbled key pairs assigned to the input and output wires of the KE gadget. Assume that E obtains the garbled label $\boldsymbol{L}^{w,A} = \boldsymbol{a} w + \boldsymbol{b} = \left( w+r, s_1(w+r)+s_2\right)$ during the evaluation, where $\boldsymbol{a} \triangleq \left( 1, s_1\right)$ and $\boldsymbol{b} \triangleq \left( r, s_1r+s_2\right)$, and $r,s_1,s_2$ are sampled by G (the precise way of sampling $r,s_1,s_2$ is instantiated per GC and it will be addressed soon). In addition, G sends E the following ciphertexts as the garbled tables:

$$ \textsf{enc}\left( s_1,\boldsymbol{c}\right) ~~~\textsf{enc}\left( s_2,-\boldsymbol{c}\cdot r+\boldsymbol{d}\right) $$

E can first utilize the linear homomorphism to obtain a new ciphertext:

then decrypts the new ciphertext using key $s_1(w+r)+s_2$ and learns $\boldsymbol{c}\cdot w + \boldsymbol{d}$. This achieves a KE gadget that can expand a length-2 garbled label to a length-n garbled label. While the paradigm is simple and elegant, instantiating it is non-trivial. This is mainly because we need to ensure $x+r$ and $s_1(x+r)+s_2$ are allowed to be revealed without compromising privacy.

BLLL’s GC for the Bounded Integer Computation. The crucial observation of the BLLL’s GC is that the AIK paradigm for bounded computation can be instantiated by carefully selecting the integer ring $\mathcal {R}$ accompanied by a customized KE gadget that is instantiated via a lightweight, customized encryption scheme defined based on the DCR assumption. Consider two large enough (e.g., 1024-bits) primes $p = 2p'+1$ and $q = 2q'+1$ of equal length,⁹ where $p',q'$ are also primes, and the corresponding RSA modulus $N = pq$. Given that the computation is B-bounded, select $B_{\textsf{e}} =B\lambda ^{\omega (1)}$, $B_{\textsf{msg}} =NB_{\textsf{e}} \lambda ^{\omega (1)}$ and some sufficiently large integer $\zeta$ such that $N^\zeta >2B_{\textsf{msg}} +1$. For a small constant $\mathrm {\Psi }$ (e.g., 10), G and E sample $\tau _1, \ldots , \tau _{\mathrm {\Psi }} \overset{\$}{\leftarrow }\left\{ a^{2N^\zeta }~|~a \in \mathbb {Z}^*_{N^{\zeta +1}}\right\}$ as part of the encryption parameters.

BLLL’s GC embeds the B-bounded integers into the integer modular ring $\mathbb {Z}_{N^\zeta }$. This is allowed because $N^\zeta > 2B+1$. Essentially, BLLL’s GC applies the AIK paradigm over $\mathbb {Z}_{N^\zeta }$ and further shows a KE gadget that can expand the garble label defined over $\mathbb {Z}_{N^\zeta }$. To achieve this, BLLL’s GC relies on an encryption scheme where the $\textsf{enc}$ algorithm takes a key $k \in \mathbb {Z}$ and a vector message $\boldsymbol{m} \in \mathbb {Z}_{N^\zeta }^{\mathrm {\Psi }}$ as input and outputs a ciphertext in $(\mathbb {Z}^*_{N^{\zeta +1}})^{\mathrm {\Psi }}$. More specifically, consider $\boldsymbol{m}=(m_1, \ldots , m_{\mathrm {\Psi }})$, procedure $\textsf{enc}$ is defined as¹⁰:

$$ \textsf{enc}(k, \boldsymbol{m}) \triangleq \left( \tau _1^k(N+1)^{2m_1}, \ldots , \tau _n^k(N+1)^{2m_n}\right) ~\text {over}~\mathbb {Z}^*_{N^{\zeta +1}} $$

Note that the order of $N+1$ within the group $\mathbb {Z}^*_{N^{\zeta +1}}$ is $N^\zeta$. The decryption procedure is done by element-wise (1) multiplication each term with $\tau _{i \in [n]}^{-k}$, and (2) solving the discrete logarithm to the base $N+1$ in the group $\mathbb {Z}^*_{N^{\zeta +1}}$, which is known to be easy [13, 35]. Moreover, this encryption scheme supports linear evaluations over keys and plaintexts. Namely, given an integer $\beta \in \mathbb {Z}$.

$$\begin{aligned} &\textsf{enc}(k_1\beta +k_2, \beta \boldsymbol{m}_1+\boldsymbol{m}_2)\\ =& \left( \tau _1^{k_1\beta +k_2}(N+1)^{2m_{1,1}\beta +2m_{2,1}}, \ldots , \tau _n^{k_1\beta +k_2}(N+1)^{2m_{1,n}\beta +2m_{2,n}}\right) \\ =& \left( \tau _1^{k_1\beta }(N+1)^{2m_{1,1}\beta }, \ldots , \tau _n^{k_1\beta }(N+1)^{2m_{1,n}\beta }\right) \\ & \otimes \left( \tau _1^{k_2}(N+1)^{2m_{2,1}}, \ldots , \tau _n^{k_2}(N+1)^{2m_{2,n}}\right) \\ =&~\textsf{enc}(k_1, \boldsymbol{m}_1)^\beta \otimes \textsf{enc}(k_2, \boldsymbol{m}_2) \end{aligned}$$

where $\otimes$ is the element-wise product over $\mathbb {Z}^*_{N^{\zeta +1}}$. Recall that we still need to address how to select $r, s_1,s_2$ in the paradigm for constructing the KE gadget we presented above. Here, for each KE gadget expanding a length-2 garbled label to a length-$\mathrm {\Psi }$ garbled label, G samples $r \overset{\$}{\leftarrow }[-B_{\textsf{e}}, B_{\textsf{e}} ]$, $s_1 \overset{\$}{\leftarrow }\{0, \ldots , N\}$ and $s_2 \overset{\$}{\leftarrow }[-B_{\textsf{msg}}, B_{\textsf{msg}} ]$. Crucially, for any $w \in [-B, B]$, (1) $w+r$ statistically hides w; and (2) $s_1(x+r)+s_2$ statistically hides $s_1(x+r)$. Hence, $x+r$ and $s_1(x+r)+s_2$ can be revealed to E.

A small subtlety arises here as the garbled labels are defined over $\mathbb {Z}_{N^\zeta }$. However, the key (and the homomorphism operation) is defined over $\mathbb {Z}$. Interestingly, this is not an issue because $N^\zeta$ is large enough and w is B-bounded. For example, since $w \in [-B,B]$, we have $w+r \in [-B-B_{\textsf{e}},B+B_{\textsf{e}} ]$. Now, since $N^\zeta > 2B+2B_{\textsf{e}} +1$, by obtaining the value $w+r \in \mathbb {Z}_{N^\zeta }$, E can recover $w+r$ value in $\mathbb {Z}$. Henceforth, we will use $(\alpha )_\mathbb {Z}$ to denote the procedure to map a value $\alpha$ in $\mathbb {Z}_{N^\zeta }$ to a value in $\mathbb {Z}$, specified by BLLL’s GC.

Finally, note that the encryption scheme above is not a standard Paillier encryption [35]. In fact, it is not even a randomized encryption. However, it is sufficient because each key is used in a single instance of $\textsf{enc}$.¹¹.

Constant-Rate Property. The constant-rate property of BLLL’s GC comes from that the garbled truth tables of the KE gadget are constant-rate. Namely, element in $\mathbb {Z}^*_{N^{\zeta +1}}$ has length $\log N^{\zeta +1}$ and:

$$\begin{aligned} \log N^{\zeta +1} &={\mathcal {O}}(\log N + \log B_{\textsf{msg}})={\mathcal {O}}(\log N + \log NB\lambda ^{\omega (1)})\\ &= {\mathcal {O}}(\log N + \log B + \omega (\log \lambda ))\\ {} &={\mathcal {O}}(\kappa + \log B) \end{aligned}$$

4 Overflow Attacks via BLLL’s GC

In this section, we demonstrate why the natural 2PC protocol for bounded integer computations, instantiated via BLLL’s GC, is not secure against a malicious adversary, corrupting either G or E. In contrast, the 2PC semi-honest protocol instantiated via Yao Boolean GC implies security against a malicious E; see a discussion in our full version regarding the reasons for these differences.

Ill-Defined Computation Model. Before showing concrete attacks, we note that B-bounded integer computation regarding malicious 2PC is not well-defined. This is because the computational model should properly define what should happen if the computation is applied to an inadmissible input (where intermediate wires overflow B). This is not required in the semi-honest setting since the definitions can condition over an admissible input. Nevertheless, what we show in this section eliminates the possibility of defining the result of computing on inadmissible inputs as $\texttt {abort}$ when instantiating the garbling scheme with the BLLL GC. Also, it is insufficient to output the computation result over $\mathbb {Z}_{N^\zeta }$.

4.1 Overflow Attacks by Malicious E: A Toy Example

We present a concrete toy example attack that explains how a malicious E$^*$ could compromise the privacy of the honest G by carefully selecting his inputs. Our attack indicates the challenges in boosting security for E beyond semi-honest. In the rest of this paper, we will only focus on a malicious G.

Consider 2PC over B-bounded integer computations where $B=2$. That is, the parties use inputs within $[-2,2]$ and compute the circuits over $\mathbb {Z}$ where all the intermediate wires fall within $[-2,2]$ as well. Recall that in BLLL’s GC, the parties need to set up some public parameters, including $B_{\textsf{e}} =B\lambda ^{\omega (1)}$. Let $\lambda = 40$ and $B_{\textsf{e}} =2^{80}$. Now, consider a circuit $\mathcal {C}$ that includes an intermediate wire w holding the value $w=(xy)^{80}$ where x is G’s input, and y is E’s input. Assume that w is used as an input of a KE gadget. Namely, E learns $w+r$ (over large enough $\mathbb {Z}_{N^\zeta }$) where r is sampled from $[-2^{80},2^{80}]$. Let the honest E hold the input $y=0$. This implies $w=0$ no matter what G inputs for x. Indeed, any $x\in [-2,2]$ with $y=0$ forms an admissible input. In particular, $w+r$ will always be just r as a uniform distribution over $[-2^{80},2^{80}]$ so E should not obtain any information on x by observing $(xy)^{80}+r$.

However, a malicious E$^*$ can simply use $\widetilde{y}=1$ as his input. Namely, $w=(x\widetilde{y})^{80}=x^{80}$. Obviously, if $x \in \{0,\pm 1\}$, $w+r$ will be within $[-B_{\textsf{e}}, B_{\textsf{e}} ]$ with overwhelming probability over r. However, if $x \in \{\pm 2\}$, $w+r$ will be within $[-B_{\textsf{e}}, B_{\textsf{e}} ]$ with probability roughly $\frac{1}{2}$ over r. Say differently, if E$^*$ observes that $w+r$ does not belong to $[-B_{\textsf{e}}, B_{\textsf{e}} ]$, he learns that $x \in \{\pm 2\}$. Thus, E$^*$ gains information about x simply by setting his input to 1 and monitoring $(x\tilde{y})^{80}+r$. We remark that $1 \in [-2,2]$, so this input is legal. We denote this attack by an overflow attack because E$^*$ compromises G’s privacy by causing an overflow by maliciously choosing his B-bounded inputs.

One might think that the above toy example is contrived. Specifically, when $B=2$, by setting $\widetilde{y}=1$, E learns whether $(x,\widetilde{y})$ is admissible. Namely, if $x \in \{0, \pm 1\}$, $(x,\widetilde{y})$ is an admissible input; otherwise, if $x \in \{\pm 2\}$, it is not. Therefore, this leakage may already be covered by the intended computation. We emphasize that the leakage of an overflow attack is beyond the intended computation. In particular, consider the same attack with $x_1,x_2,y_1,y_2$ where there are wires $w_1 = (x_1y_1)^{80}$ and $w_2 = (x_2y_2)^{80}$. By changing the honest input $(y_1,y_2)=(0,0)$ to $(\widetilde{y_1},\widetilde{y_2})=(1,1)$, E can use overflow to distinguish the following three cases regarding G’s inputs $(x_1, x_2)$: (a) $(\{0,\pm 1\},\{\pm 2\})$, (b) $(\{\pm 2\}, \{0, \pm 1\})$, or (c) $(\{\pm 2\}, \{\pm 2\})$. This leakage is beyond learning whether $((x_1,x_2), (1,1))$ is an inadmissible input, which does not help to distinguish the above three cases. We conclude with the following remark:

Remark 1

(Generality). The above example can be generalized to any bound B. Consider $B_{\textsf{e}} =B^{2\lambda }$ and a circuit $\mathcal {C}$ where there exists an intermediate wire $w=(xy)^{2\lambda }$ such that x is G’s input, y is E’s input and $y=0$ in the honest case. By injecting $\widetilde{y}=1$, a malicious E$^*$ can gain information regarding the range of x based on whether $w+r$ overflows $B_{\textsf{e}}$, which should not happen when $y=0$ because $w+r$ should be uniform and always bounded by $B_{\textsf{e}}$. Note that this attack is not restricted to a power of xy and is feasible for other computations.

Notably, the overflow attack breaks privacy but may also harm correctness, as it may prevent E$^*$ from obtaining the correct next garbled labels. Nevertheless, in some cases, the overflow does not prevent E$^*$ from continuing to evaluate the KE gadgets. To further see this point, recall that the garbled tables of a KE gadget (for a single entry) are of the form:

$$ \tau ^{s_1}(N+1)^{2c_1}~~~\tau ^{s_2}(N+1)^{-2c_1r+2d_1}~~~\text {over}~\mathbb {Z}^*_{N^{\zeta +1}} $$

where the garbled label of the input obtained by E will be:

$$ w+r~~~s_1(w+r)+s_2~~~\text {over}~\mathbb {Z}_{N^{\zeta }} $$

In the honest execution, E can recover $w+r$ and $s_1(w+r)+s_2$ from the $\mathbb {Z}_{N^{\zeta }}$ domain and use homomorphism to obtain $c_1w+d_1$ over $\mathbb {Z}_{N^{\zeta }}$, as the garbled output labels of the KE gadget. Now, when an overflow happens, recovering $w+r$ and $s_1(w+r)+s_2$ can be more challenging as they may wrap around the domain of $\mathbb {Z}_{N^{\zeta }}$. Nevertheless, it does not mean that E$^*$ fails to recover these values since the wrapping may be small and E$^*$ can just brute force it.

An interesting case happens when w indeed overflows over integers, however, due to the computation being taken over the ring $\mathbb {Z}_{N^\zeta }$, it wraps around the space and ends up as $[-B,B]$ over $\mathbb {Z}_{N^\zeta }$. In this case, a malicious E$^*$ cannot detect whether an overflow occurred regardless of the choice of randomness $r,s_1,s_2$. We denote this type of overflow an undetectable overflow. It is easy to see that, in this case, the security of a malicious E$^*$ can be reduced to the privacy of BLLL’s GC since the simulator can use the simulator of BLLL’s GC to generate faked garbled tables and faked garbled labels of inputs.

Given the above discussion, a malicious E may learn ${\mathcal {O}}(|\mathcal {C} |)$ leaked bits regarding G’s inputs since he can observe whether each wire overflows. In our full version, we include a conjecture (strongest) ideal world that captures the 2PC naïvely instantiated via BLLL’s GC for a malicious E.

4.2 Overflow Attacks by Malicious G: The Lower Bound

We already presented how a malicious E can utilize overflow attacks to compromise the privacy of the honest G’s inputs. Indeed, a malicious G can also launch a similar attack by using some legal B-bounded inputs, even while providing a correct BLLL’s GC. However, the consequence of this attack changes.

Consider a malicious G$^*$ that provides a correct garbled BLLL’s GC but uses some bad inputs. In this case, G$^*$ may observe whether the honest E aborts the execution, which implies whether an overflow occurred, even without identifying the precise wire that overflowed. Note that aborting the execution may be inevitable because E may not be able to evaluate the KE gadget when the overflow is too large. This attack rules out achieving full security against a malicious G since this abort event is correlated with E’s input. More precisely, the best security notion we can hope to achieve in the presence of a malicious G is security with leakage. In this work, we observe that this leakage can be as small as only 1-bit, capturing the malicious G attacks. That is, a malicious G cannot change the intended computation circuit but rather learn whether E aborted.

Leakage Class of Predicates in the Presence of a Correct GC. Recall that 1-bit leakage is captured by allowing the ideal adversary to submit a leakage predicate. We first analyze what class of leakage predicates can be submitted if we assume that the malicious G$^*$ constructs a correct BLLL’s GC, which naturally serves as a lower bound on the class of leakage predicates that a malicious 2PC protocol via BLLL’s GC can tolerate as the attacks are only selective due to bad inputs.

Note that the only parameters G$^*$ can specify for each KE gadget are $r, s_1, s_2$. Now, since the BLLL’s GC is constructed correctly, E must obtain the garbled labels $(L_0, L_1) = (w+r, s_1(w+r)+s_2)$ for the input wire of the KE gadget, where w is a value defined by the circuit $\mathcal {C}$. If either $L_0$ or $L_1$ overflows, E aborts. We notice that when $r,s_1,s_2$ are selected within the correct bounds (see Sect. 3), even if the computation can wrap around the domain $\mathbb {Z}_{N^\zeta }$, a well-bounded $L_0$ implies a well-bounded $L_1$. Here, the well-bounded notion includes the scenario of undetectable overflows. I.e., $w+r \in [-B-B_{\textsf{e}} +N^\zeta T, B+B_{\textsf{e}} +N^\zeta T]$ for some integer T. Moreover, when E decodes these two values in $\mathbb {Z}$ as $(L_0)_{\mathbb {Z}}$ and $(L_1)_{\mathbb {Z}}$, it implies that E can use $(L_1)_{\mathbb {Z}}$ as the key to correctly decrypt $\mathrm {\Psi }$ ciphertexts:

$$ \left\{ (\tau _i^{s_1}(N+1)^{2c_i})^{(L_0)_{\mathbb {Z}}}\cdot (\tau _i^{s_2}(N+1)^{-2c_ir+2d_i})\right\} _{i \in [\mathrm {\Psi }]} $$

where $(\boldsymbol{c}, \boldsymbol{d})$ are the garbled key pair of the output wire of this KE gadget, and $\tau _1,\ldots ,\tau _{\mathrm {\Psi }}$ are public parameters sampled from $\left\{ a^{2N^\zeta } | a \in \mathbb {Z}^*_{N^{\zeta +1}}\right\}$ (which will be reused across different KE gadgets). Thus, E aborts if and only if $L_0$ overflows. Hence, the predicate that the ideal malicious G can submit to the ideal functionality is a disjunction of the following predicate clauses:

• For each KE gadget¹² over wire $w=w(\boldsymbol{x},\boldsymbol{y})$ defined by the circuit $\mathcal {C}$, a malicious G can select $r \in [-B_{\textsf{e}}, B_{\textsf{e}} ]$ to add a clause checking whether:

  $$\begin{aligned} L_0(\boldsymbol{x}, \boldsymbol{y}) \triangleq w(\boldsymbol{x},\boldsymbol{y})+r \overset{?}{\in }\ [-B-B_{\textsf{e}}, B+B_{\textsf{e}} ]~\text {over}~\mathbb {Z}_{N^\zeta }. \end{aligned}$$

Note that the above leakage predicate is a disjunction of small predicate clauses. In particular, if there are two wires being overflowed, while there are 2 clauses being set to 1, the adversary can only learn that there exists at least one 1-clause.

Enlarging the Class of Leakage Predicates by Relaxing Correctness. Ensuring correct garbling with respect to the above class of leakage predicates is challenging. In this work, we circumvent this difficulty by allowing a larger class of predicates, where the leakage a malicious G can obtain remains a single bit.

Specifically, we present in Sect. 5 a non-trivial 2PC protocol via BLLL’s GC that is secure against a malicious G with 1-bit leakage, preserving constant-rate with low cost. This comes at the price of tolerating a slightly larger class of 1-bit leakage predicates. The crucial observation lies in allowing G to inject some small errors inside GC, which will not affect the correct evaluation if E does not abort. In other words, we will only force a malicious G to provide an almost correct BLLL’s GC rather than a fully correct one. We observe that if we can force G to provide garbled tables (of a KE gadget) that encrypt the correct intended plaintexts, it is already sufficient to ensure that E will obtain a correct garbled label for the KE output wire. In slightly more detail, recall that the garbled tables of a KE gadget (for a single entry) are of the form:

$$ \tau ^{s_1}(N+1)^{2c_1}~~~\tau ^{s_2}(N+1)^{-2c_1r+2d_1}~~~\text {over}~\mathbb {Z}^*_{N^{\zeta +1}} $$

where $(c_1,d_1)$ is one entry of the garbled output key pair and $r,s_1,s_2$ are selected by G. Assume that E holds the garbled input label $(L_0, L_1) = (w+r,s_1(w+r)+s_2)$ over $\mathbb {Z}_{N^\zeta }$. We notice that if we can ensure that (1) $L_0$ equals to $w+r-N^\zeta T$ for some integer T (i.e., a correct input garbled label); and (2) the garbled tables encrypt the values $2c_1$ and $-2c_1r+2d_1$, then we have:

$$\begin{aligned} (L_0)_\mathbb {Z} = w+r-N^\zeta T - N^\zeta t~\text {where}\, t \in \{0, 1\}\\ (N+1)^{2c_1(L_0)_\mathbb {Z}}\cdot (N+1)^{-2c_1r+d_1}=(N+1)^{2c_1w+d} \end{aligned}$$

since $\textsf{ord}(N+1)=N^\zeta$ in $\mathbb {Z}^*_{N^{\zeta +1}}$. This implies that E must obtain $c_1w+d$ as the garbled output label of the KE gadget given that E can decrypt the ciphertext, which already provides a correct KE gadget. Namely, G cannot force E to output an ill-formed garbled label (e.g., $w+1$). As a result, we do not need to force G to provide bounded $r,s_1,s_2$ or even bind $s_1,s_2$ within $\tau ^{s_1}, \tau ^{s_2}$ in the garbled tables. We remark that additional details to explain why this is true, e.g., how to ensure E obtains a correct $L_0$ and how we utilize this fact, will be covered and discussed explicitly in Sect. 5. Informally, since the garbled labels are defined over $\mathbb {Z}_{N^\zeta }$ and the order of $N+1$ is also $N^\zeta$ modulus $\mathbb {Z}^*_{N^{\zeta +1}}$, we can operate over the space $\mathbb {Z}_{N^\zeta }$ to “authenticate” an almost correct BLLL’s GC.

We conclude this discussion by emphasizing that an almost correct BLLL’s GC will allow a malicious G to specify a leakage predicate of a slightly larger class than the one induced by a fully correct BLLL’s GC. This is because a malicious G can further select unbounded $r,s_1,s_2$ and use ill-formed multiplication terms $\tau ^{s_{i \in [2]}}$ in the garbled tables to trigger E’s abort. Note that this implies that the leakage predicate will include more clauses but will still be defined as a disjunction. Namely, our protocol complements the lower bound of 1-bit leakage but leaves a gap concerning the minimal leakage predicate class. Given that the GMW compiler, instantiated with succinct proofs, can complement this tighter leakage class of predicate (again, with an undesirable non-black-box computation cost), we leave it as a valuable open problem to extend our protocol to support the tighter leakage predicate class or show that this expansion on the leakage predicate class is harmless. We will further discuss the challenges in Sect. 5.

5 Secure Two-Party Computation over Bounded Integer Computations for Malicious G with 1-Bit Leakage

We formally describe how to design secure two-party computation for bounded integer computation based on BLLL GC and several non-trivial correctness mechanisms to achieve malicious security for G with 1-bit leakage. Informally, our protocol forces G to provide an almost correct BLLL’s GC (see Sect. 4.2).

Deferred Proofs. All proofs are deferred to our full version [21].

5.1 IT-MACs over $\mathbb {Z}_{N^\zeta }$

Our protocol requires G to commit the randomness she used to select the garbled key pairs for each wire. As the garbled key pairs of two different wires can be correlated (e.g., the garbled key pairs of an input and an output wires of a multiplication gate), we use ZK proofs to ensure the correctness of the GC. To run these proofs, G and E should be able to perform some basic operations over the commitments, instantiated by VOLE correlation.

IT-MAC Commitments over $\mathbb {Z}_{N^\zeta }$. VOLE correlations (see Fig. 1) can be viewed as random Information Theoretic Message Authentication Codes (IT-MACs) [9, 34]. An IT-MAC of $x \in \mathbb {Z}_{N^\zeta }$ is a correlated distributed tuple where G holds a value x and a MAC of x as $\textsf{mac}(x) \overset{\$}{\leftarrow }\mathbb {Z}_{N^\zeta }$, and E holds a global key¹³ $\varDelta \overset{\$}{\leftarrow }\mathbb {Z}_{N^\zeta }$ and a local key of x as $\textsf{key}(x) = x\varDelta +\textsf{mac}(x)$. We denote the IT-MAC of x as $[x]_\varDelta = \langle \textsf{mac}(x), x; \textsf{key}(x)\rangle$ or [x]. Each VOLE correlation over $\mathbb {Z}_{N^\zeta }$ is an IT-MAC [r] where r is a uniform sample. A random IT-MAC [r] can be “consumed” and updated into an IT-MAC [x] using a standard technique [8]. Namely, G can send $x-r$ to E, and then both parties can adjust [r] to [x]. IT-MACs (in particular, over $\mathbb {Z}_{N^\zeta }$) hold the following notable properties:

• Perfect hiding: For [x], $\textsf{key}(x)$ and $\varDelta$ include no information among x since $\textsf{key}(x)$ is one-time padded by a uniform $\textsf{mac}(x)$.

• Statistical binding: For [x], G can open it by sending $x, \textsf{mac}(x)$ where E can check $\textsf{key}(x) \overset{?}{=}\ x\varDelta +\textsf{mac}(x)$. A malicious G can only open x to a different value $x'$ with probability up to $\frac{1}{p}$ as proven in Lemma 1. This is sufficient for our security argument since p is a large enough prime (in $\lambda$).

• Linear homomorphism: IT-MACs can be linearly evaluated locally as:

  • Holding [x] and [y], two parties can locally generate $[x+y]_\varDelta$ as $\langle \textsf{mac}(x)+\textsf{mac}(y), x+y; \textsf{key}(x)+\textsf{key}(y) \rangle$.

  • Holding $c \in \mathbb {Z}_{N^\zeta }$, two parties can locally generate $[c]_\varDelta$ as $\langle 0, c; c \varDelta \rangle$.

  • Holding $c \in \mathbb {Z}_{N^\zeta }$ and [x], two parties can locally generate [cx] as $\langle c \cdot \textsf{mac}(x), c x; c \cdot \textsf{key}(x)\rangle$.

Lemma 1

(Statistical Binding for IT-MACs over $\mathbb {Z}_{N^\zeta }$). Let $N=pq$ be an RSA modulus where $p < q$ and $\zeta \in \mathbb {Z}^+$. An IT-MAC [x] over $\mathbb {Z}_{N^\zeta }$ can only be opened to a different value $x' \ne x$ with probability up to $\frac{1}{p}$.

Zero-Knowledge Proofs for Multiplication Triples of IT-MACs over $\mathbb {Z}_{N^\zeta }$. While G and E can evaluate IT-MACs linearly without communication, in our protocol, we also need G and E to multiply two IT-MACs. This can be done by the standard commit-and-prove paradigm. Formally, this means that G and E holding [x], [y], [z] over $\mathbb {Z}_{N^\zeta }$ where G needs to convince E in ZK that $z=x y$. While there are many different techniques to do this, e.g. [6, 15, 40], we find that a technique called Line-point Zero-Knowledge (LPZK) over fields [15] can also support rings $\mathbb {Z}_{N^\zeta }$. LPZK only requires 2 ring elements of communications to prove each multiplication triple. We note that the LPZK does not directly work for some rings, e.g., $\mathbb {Z}_{2^k}$ (see [5]). We defer the details of LPZK to our full version. Crucially, it relies on Lemma 2 to achieve a $\frac{2}{p}$ soundness error.

Lemma 2

(Number of Roots for Quadratic Equations over $\mathbb {Z}_{N^\zeta }$). Let $N=pq$ be an RSA modulus where $p < q$ and $\zeta \in \mathbb {Z}^+$. For any $a, b, c \in \mathbb {Z}$ such that $N^\zeta \not \mid a$, the following equation has at most $2p^{\zeta -1}q^\zeta$ solutions.

$$\begin{aligned} a\chi ^2+b\chi +c \equiv 0 \pmod {N^\zeta } \end{aligned}$$

(1)

In summary, in the $\mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }$-hybrid, G and E can:

• Generate IT-MAC [r] from $\mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }$ where r is uniform and unknown to E.

• Generate IT-MAC [x] where x is G-chosen by communicating 1 element.

• Open IT-MAC [x] to x by communicating 2 elements.

• Perform linear operations over IT-MACs for free.

• Obtain IT-MAC [xy] given [x] and [y] by communicating 3 elements.

The communication of the above operations is uni-directional once the VOLE correlations are generated. The computation complexity for both parties is ${\mathcal {O}}(1)$ additions/multiplications in $\mathbb {Z}_{N^\zeta }$. We conclude by remarking that our arguments hold only when G has no knowledge of $\varDelta$, which is the case in our protocol.

5.2 Protocol to Bind IT-MACs with Key Extension Gadgets

The operations presented in Sect. 5.1 allow G and E to perform additions and multiplications on the IT-MACs. However, to garble a circuit as in BLLL’s GC, G must also use the randomness committed within the IT-MACs to construct the garbled tables of KE gadgets. Clearly, a malicious G can provide badly generated garbled tables, so we need to design a mechanism to force G to use the committed randomness. Recall that for KE gadgets (see Sect. 3), G sends ciphertexts Cs defined over $\mathbb {Z}^*_{N^{\zeta +1}}$. Let the public parameter $\tau$ be $\tau \overset{\$}{\leftarrow }\{a^{2N^\zeta } | a \in \mathbb {Z}^*_{N^{\zeta +1}}\}$ then, each ciphertext C is defined as¹⁴ $\tau ^s\cdot (N+1)^m~\text {over}~\mathbb {Z}_{N^{\zeta +1}},$ where s and m are determined (over $\mathbb {Z}_{N^\zeta }$) by the randomness of G. Therefore, s and m can also be committed within the IT-MACs as [s] and [m]. We now present a protocol to ensure that G indeed uses [m] to construct the garbled tables for the KE gadgets. We note that a malicious G can use a different [s] or even an element in $\mathbb {Z}_{N^{\zeta +1}}$ that is not generated by $\tau$. In Sect. 4.2, we have already informally justified why the evaluator does not need to monitor this attack, and why it affects neither privacy (up to 1 bit of leakage) nor correctness. Our observation is crucial for feasibility and reducing communication overhead, which leads to a non-trivial $\varSigma$-protocol formalization discussed below.

Remark 2

(A gap between soundness and correctness). Our special-purpose object (Definition 1) can be viewed as a customized interactive proof rather than a classical one. More specifically, unlike a classical proof, the language recognized by the correctness property in our customized interactive proof is a subset of the language recognized by the soundness property. That is, given $[s], [\varGamma ], C$, correctness holds for $C=\tau ^s(N+1)^{\varGamma }$, while soundness only prevents a malicious G$^*$ from using $C=C_U(N+1)^{\varGamma '}$ where $C_U \in U$ and $\varGamma ' \ne \varGamma$. In particular, for a $C=C_U(N+1)^\varGamma$ where $C_U \in U$, our definition does not explicitly say whether E will output C. Say differently; we only need to prevent a malicious G$^*$ from using a ciphertext (i.e., the KE gadget) that encrypts a wrong message but not using a wrong key. This suffices since (1) a corrupting key will only cause up to 1-bit leakage, and (2) a correct message ensures a correct execution.

Before continuing with the definition and protocol, we recall the decomposition property of an element in $\mathbb {Z}^*_{N^{\zeta +1}}$.

LU decomposition over $\mathbb {Z}^*_{N^{\zeta +1}}$. Recall that $\mathbb {Z}^*_{N^{\zeta +1}}$, is a direct product $L \times U$, where L is the cyclic of order $N^\zeta$ generated by $(N+1)$ and U is isomorphic to $\mathbb {Z}^*_N$ of order $(p-1)(q-1)$. That is, given an element C in $\mathbb {Z}^*_{N^{\zeta +1}}$, it can be uniquely decomposed into $C_L \in L$ and $C_U \in U$ such that $C_L \cdot C_U = C$. Moreover, $C_L = (N+1)^{k_C}$ for some unique $k_C \in \mathbb {Z}_{N^\zeta }$. We define auxiliary functions $\textsf{LU}$, returning $C_L, C_U$ given an element $C \in \mathbb {Z}^*_{N^{\zeta +1}}$, and $\textsf{LU}_k$ that outputs the discrete logarithm of $C_L$ to the base $N+1$¹⁵. Clearly, for any $C \in \mathbb {Z}^*_{N^{\zeta +1}}$, let $(C_L, C_U) := \textsf{LU}(C)$, we have $\textsf{LU}_k(C_L) = \textsf{LU}_k(C)$ and $\textsf{LU}_k(C_U) = 0$.

Special-purpose $\varSigma$-protocol in the VOLEc-hybrid. To ensure correctness on the garbler’s side, we abstract out the following guarantees. Assume that G and E hold an IT-MAC $[\varGamma ]$ and an element $C \in \mathbb {Z}^*_{N^{\zeta +1}}$ generated by the KE gadget forwarded from G. Then G can convince E in ZK that $\textsf{LU}_k(C) = \varGamma$. The syntax and security properties of this cryptographic object are defined in Definition 1.

Definition 1

(Special-purpose $\varSigma$-protocol in the VOLEc-hybrid). G and E have access to all public parameters $\textsf{pp}$ including $\lambda , N=pq, \zeta , \tau \overset{\$}{\leftarrow }\left\{ a^{2N^\zeta } | a \in \mathbb {Z}^*_{N^{\zeta +1}}\right\}$ and an ideal access to $\mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }$ (Fig. 1) where $\mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }$ outputs a global key $\varDelta \in \mathbb {Z}_{N^\zeta }$ to E. G and E hold an IT-MAC $[\varGamma ]_\varDelta \in \mathbb {Z}_{N^\zeta }$ (which is generated from the basic IT-MAC operations presented in Sect. 5.1, and in particular, only requires communication from G to E), and G has an additional input $s \in \mathbb {Z}_{N^\zeta }$. Interactive PPT algorithms $\langle G^{\textsf{pp}, \mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }}([\varGamma ], s), E^{\textsf{pp}, \mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }}([\varGamma ])\rangle$ form a special-purpose $\varSigma$-protocol (for KE gadgets) in the VOLEc-hybrid (or in short, SP $\varSigma$-protocol), if after the execution, G outputs nothing and E outputs either $\texttt {abort}$ or $C \in \mathbb {Z}^*_{N^{\zeta +1}}$, and the following properties hold.

• 1. Correctness. A special-purpose $\varSigma$-protocol (for KE gadgets) in the VOLEc-hybrid is correct if

  $$ {\text {Pr}} \left[ \langle G^{\textsf{pp}, \mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }}([\varGamma ], s), E^{\textsf{pp}, \mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }}([\varGamma ])\rangle = \tau ^s(N+1)^\varGamma \right] =1 $$

• 2. Statistical soundness. A special-purpose $\varSigma$-protocol (for KE gadgets) in the VOLEc-hybrid is sound if, for any malicious algorithm $G^*$

  

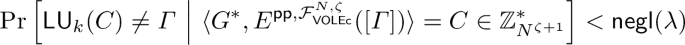
  where $\textsf{negl}(\cdot )$ is some negligible function.

• 3. Statistical honest verifier zero-knowledge (SHVZK). A special-purpose $\varSigma$-protocol (for KE gadgets) in the VOLEc-hybrid is SHVZK if there exists a PPT algorithm $\mathcal {S} ^E$ that takes public parameters $\textsf{pp}$, E’s inputs, and $\tau ^s(N+1)^\varGamma ~\text {over}~\mathbb {Z}^*_{N^{\zeta +1}}$ as inputs that can output a view satisfying:

  

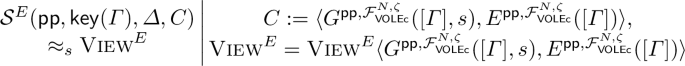
Remark 3

(Coping with multiple correlated instances). In Definition 1, we say G and E hold an IT-MAC $[\varGamma ]$. Formally, this means that G and E agree on some IT-MAC tuple generated by the operations defined in Sect. 5.1, which only requires uni-directional communication from G to E in the VOLEc-hybrid. Note that G and E can hold many other IT-MACs besides $[\varGamma ]$ while they should not affect the correctness/security properties. E.g., even though a malicious G$^*$ can have many instances of IT-MACs, this should not break the soundness. Informally, this is because the VOLE correlations G$^*$ received from $\mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }$ are independent of the global key $\varDelta$ held by E, as each VOLE correlation is one-time padded by a uniform sample (i.e., the local key chosen by $\mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }$).

Our SP $\varSigma$-protocol shares similarities with the classic discrete logarithm proof [38], where the differences are (1) there are two bases $\tau$ and $N+1$, and (2) we need to bind G’s discrete logarithm on $N+1$ to $[\varGamma ]$. We adjust Schnorr’s protocol as follows: (1) G needs to provide two answers for the random challenge from E, one for the base $\tau$ and one for the base $N+1$, and (2) G also needs to open the IT-MAC to authenticate its answer with respect to the base $N+1$. We formally define the protocol in Fig. 3 and the security claim in Theorem 2. We remark that since G needs to reply with $\nu s+\sigma$ over $\mathbb {Z}$ and s must be kept private, $\sigma$ has to be sampled from a large enough domain such that $\nu s + \sigma$ statistically hides $\nu s$. Note that $\nu s \in \{0, \ldots , (N^\zeta -1)^2\}$ over $\mathbb {Z}$, and we can select $\sigma$ from $\{0, \ldots , B_{\mathsf {\sigma }} \}$ where $B_{\mathsf {\sigma }} = N^{2\zeta }\lambda ^{\omega (1)}$. Essentially, this does not affect the rate.

Fig. 3.

Special-purpose $\varSigma$-protocol in the VOLEc-hybrid

Theorem 2

Protocol in Fig. 3 is a SP $\varSigma$-protocol in the VOLEc-hybrid per Definition 1 with the following efficiency features: ${\mathcal {O}}(1)$ communication in $\mathbb {Z}^*_{N^{\zeta +1}}$, ${\mathcal {O}}(1)$ computation of exponentiation in $\mathbb {Z}^*_{N^{\zeta +1}}$, and 3 rounds.

Parallel SP $\varSigma$-Protocol Instances. Our 2PC protocol requires multiple parallel instances of the SP $\varSigma$-protocol. Indeed, this can be done directly with multiple parallel instances of the protocol defined in Fig. 3 where E issues a new random challenge $\nu$ per instance.¹⁶ We observe that $\nu$ can be reused across different parallel instances simply because each check performed by E is done separately. For completeness, see our full version for the formal definition.

Sufficiency of Binding Only Discrete Logarithm to the Base $N+1$. Consider the event that E outputs $C \in \mathbb {Z}^*_{N^{\zeta +1}}$ and let $(C_L, C_U) := \textsf{LU}(C)$.¹⁷ Indeed, the soundness of this protocol only guarantees that $(N+1)^\varGamma = C_L$ and does not guarantee that $\tau ^s = C_U$. This is what we refer to as an almost correct BLLL’s GC in Sect. 4.2. Looking ahead, this is the only place where a malicious G can inject errors in BLLL’s GC to specify a leakage predicate. Recall that this does not weaken the 1-bit leakage privacy as it guarantees that the KE gadget will operate correctly, as formally defined in Lemma 3.

Lemma 3

(Almost Correct KE Gadgets). Given two ciphertexts $CT _0, CT _1 \in \mathbb {Z}^*_{N^{\zeta +1}}$ of some KE gadget, which is used to encode the entry $(c_1,d_1)$ of the output garbled key pair where $c_1,d_1 \in \mathbb {Z}_{N^\zeta }$. Let $( CT _{0, L}, CT _{0, U}) := \textsf{LU}( CT _0)$ and $( CT _{1, L}, CT _{1, U}) := \textsf{LU}( CT _1)$. If $\textsf{LU}_k( CT _0) = c_1$ and $\textsf{LU}_k( CT _1) = -c_1r+d$ where $r \in \mathbb {Z}_{N^\zeta }$, assume that E obtains $(L_0 = w+r,\epsilon )$ over $\mathbb {Z}_{N^\zeta }$ as the garbled label of this KE gadget input, conditioned on E not aborting. Then E must obtain $c_1w+d_1$ over $\mathbb {Z}_{N^\zeta }$ as the garbled label of this KE gadget output, independent of the concrete values within $CT _{0, U}, CT _{1, U}, \epsilon , r$.

Challenges for Achieving a Fully Correct KE. Recall that our protocol complements the lower bound of 1-bit leakage but does not meet the minimal class leakage predicate. To bridge this gap, it is sufficient to upgrade our almost correct KE gadget to a fully correct one. See our full version for the challenges behind upgrading our protocol to achieve this, which we pose as open problems.

5.3 Our 2PC Protocol

We are now ready to present our 2PC protocol for bounded integer computations instantiated by BLLL’s GC. Due to space limitations, we focus on the key components and defer additional details to  our full version.

Generating the Public Parameters. Our protocol starts with securely generating the public parameters for establishing the trusted setup (e.g. [17] for securely generating RSA modulus). We refer readers to [3] for the details on selecting these parameters. Besides the public parameters for BLLL’s GC, G and E need to generate the public parameters for the special-purpose $\varSigma$-protocol we presented in Sect. 5.2. Overall, for a given security parameter $\lambda$ and bound $B=B(\lambda )$, G and E jointly sample the following public parameters:

• 1. A sufficiently large RSA modulus $N=pq$.

• 2. A bound $B_{\textsf{e}} = B\lambda ^{\omega (1)}$; a bound $B_{\textsf{msg}} = NB_{\textsf{e}} \lambda ^{\omega (1)}$.

• 3. A sufficiently large integer $\zeta$ such that $N^\zeta > 2B_{\textsf{msg}} + 1$.

• 4. A bound $B_{\mathsf {\sigma }} = N^{2\zeta }\lambda ^{\omega (1)}$.

• 5. $\tau _1, \ldots , \tau _{\mathrm {\Psi }} \overset{\$}{\leftarrow }\left\{ a^{2N^\zeta }~|~a \in \mathbb {Z}^*_{N^{\zeta +1}}\right\}$ where $\mathrm {\Psi }$ is a constant (e.g., 10).

These public parameters are selected before the circuit $\mathcal {C}$ is known. In particular, they are independent of the circuit size $|\mathcal {C} |$ and can be reused across several instances of (different) B-bounded circuits.

Fig. 4.

The authenticated VOLE functionality

Authenticated VOLE. Similar to the role of oblivious transfer (OT) in Yao’s GC protocol, G and E use VOLE for E to learn his garbled input labels, even in the semi-honest case. Recall that in the VOLE functionality (over $\mathbb {Z}_{N^\zeta }$), G holds two length-n vectors $\boldsymbol{u}_0, \boldsymbol{u}_1$ and E holds an input x, where E learns $\boldsymbol{u}_0x+\boldsymbol{u}_1$. To further force G to use consistent garbled key pairs with the IT-MACs (i.e., G and E hold $[\boldsymbol{u}_0], [\boldsymbol{u}_1]$), we need a slightly modified version of VOLE. Namely, G holds two extra length-n vectors $\boldsymbol{w}_0, \boldsymbol{w}_1$ and E holds $\varDelta$ (the global key of the IT-MACs), where E learns $\boldsymbol{u}_0\varDelta +\boldsymbol{w}_0$ and $\boldsymbol{u}_1\varDelta +\boldsymbol{w}_1$. Note that these two vectors are exactly the local key vectors of the IT-MACs held by E (i.e., $\textsf{key}(\boldsymbol{u}_0)$ and $\textsf{key}(\boldsymbol{u}_1)$), where E can abort if G cheats by providing wrong garbled key pairs (which are not authenticated using the IT-MACs). Figure 4 presents this functionality. In this work, we do not instantiate this functionality but use it as a hybrid¹⁸. We emphasize that our protocol only uses this functionality with length vectors proportional to the input size, independent of the circuit size.

Sub-procedure: $\textsf{Expand}$. Our protocol makes function calls to a sub-procedure $\textsf{Expand}$. Essentially, this sub-procedure packs the (recursively used) KE gadgets of BLLL’s GC into a parallel SP $\varSigma$-protocol. The sub-procedure implements three algorithms:

• $\mathsf {Expand.Gb}$: This is a sub-protocol capturing the generation of garbled tables of each KE gadget. Compared to BLLL’s GC, the difference lies in that G will also prepare the messages related to the commit phase of the parallel SP $\varSigma$-protocol. The communication is uni-directional from G to E. E will abort w.h.p. if G tries to cheat in operating IT-MACs.

• $\mathsf {Expand.Sigma}$: This is a sub-protocol capturing the challenge and response phases of the parallel SP $\varSigma$-protocol. Essentially, this happens after all $\mathsf {Expand.Gb}$s finish. The communication is uni-directional from G to E after E issues a single uniform challenge. Note that the random challenge can be replaced by the Fiat-Shamir heuristic [16] assuming random oracle (RO). E will abort w.h.p. if some garbled table of a KE gadget provided by G (in a call to $\mathsf {Expand.Gb}$) is not almost correct.

• $\mathsf {Expand.Ev}$: This is a sub-procedure used by E only to (recursively) evaluate KE gadgets. Compared to BLLL’s GC, the difference lies in that E will abort if E detects some errors (e.g., overflow or inability to evaluate).

See our full version for the fined-grained descriptions and formalization.

Our protocol $\mathrm {\Pi }$: primary components. We formalize our protocol algorithmically. G and E start with public parameters, a circuit $\mathcal {C}$ as a sequence of tuples under the standard gate-by-gate representation. We only consider single-output circuits to simplify the presentation, but our protocol can be trivially generalized to multiple outputs. Our protocol $\mathrm {\Pi }$ is composed of three primary components:

• 0. G and E generate VOLE correlations. In Step 0 (embedded in the first primary component in Fig. 5), G and E instantiate the VOLE correlation functionality over $\mathbb {Z}_{N^\zeta }$ to generate enough (pseudo-)random VOLE instances. These VOLE correlations are used as (pseudo-)random IT-MACs, to set up a pool of committed randomness that G and E can consume. The overall number of VOLE correlations required by the parties need is ${\mathcal {O}}(|\mathcal {C} |)$. This step is a circuit-independent pre-processing phase.

• 1. G garbles an almost correct BLLL’s GC (see Fig. 5). In the first primary component, G generates a BLLL’s GC in an authenticated manner. Step 1 is adjusted from the BLLL’s GC garbling procedure – the difference lies in that each operation insides is replaced by either an IT-MAC operation or the commit phase of the parallel SP $\varSigma$-protocol (captured by sub-protocol $\mathsf {Expand.Gb}$). Step 1 only requires uni-directional communication from G to E. Step 2 captures the challenge and response phases of the parallel SP $\varSigma$-protocol (captured by sub-protocol $\mathsf {Expand.Sigma}$), which requires a round-trip communication. By Fiat-Shamir transform, assuming RO, this can be achieved with uni-directional communication from G to E. If E aborts in the first component, the abort is independent of E’s inputs; otherwise, it means that E holds an almost correct BLLL’s GC.

• 2. E obtains the garbled labels of the input (see Fig. 6a). In the second primary component, E obtains garbled labels of inputs of $\mathcal {C}$. In this component, E can abort if G fails to provide correct garbled labels generated from the committed garbled key pairs. The communication is uni-directional from G to E in the $\mathcal {F}_{\textsf{aVOLE}}^{N,\zeta }$-hybrid model. If E aborts in the second component, the abort is independent of E’s inputs.

• 3. E evaluates the circuit (see Fig. 6b). E evaluates the GC as BLLL’s GC. The difference lies in E may abort if E catches overflows on garbled labels or incorrectly evaluates some KE gadget (captured by sub-protocol $\mathsf {Expand.Ev}$). The communication is uni-directional from E to G. If E aborts in the third component, the abort depends on E’s inputs.

See our full version for the fined-grained descriptions.

Fig. 5.

The first component of our protocol $\mathrm {\Pi }$. Note that Eqs. (2) to (4) are the same as add/mult gadgets from the AIK paradigm presented in Fig. 2.

Fig. 6.

The second and third components of our protocol $\mathrm {\Pi }$

Proof Overview. The security of $\mathrm {\Pi }$ can be shown using the following arguments:

Correct Execution (see Lemma 4). Intuitively, to argue our protocol is secure against malicious G with 1-bit leakage, we need to argue: if E does not abort and output $res$, $res$ w.h.p. must be calculated using the malicious G’s chosen inputs $\widetilde{\boldsymbol{x}}$ and E’s inputs $\boldsymbol{y}$ over the intended computation $\mathcal {C}$. I.e., a malicious G cannot forge the intended computation task. Informally, this is because if G does not use an almost correct BLLL’s GC, she will be caught before E starts the evaluation, i.e., before the third component of $\mathrm {\Pi }$. Conditioned over the GC is almost correct, we need to argue that the garbled labels obtained by E are “well-formed”. Namely, they indeed encode a value generated from committed garbled key pairs. This trivially holds because we require G (1) to prove the correctness of the committed IT-MAC values related to E’s input garbled key pair (see Step 3); (2) to open IT-MACs of gabled labels of her inputs (see Step 4).

Well-Defined Leakage Predicate. Note that E’s abort before evaluation (i.e., the third component of $\mathrm {\Pi }$) is independent of E’s inputs. Thus, the leakage predicate is well-defined by the evaluation procedure of BLLL’s GC. In particular, a malicious G$^*$ can choose some parameters (i.e., errors in an almost correct GC). Note that these parameters can be extracted by a simulator because all the randomness G$^*$ used is committed under IT-MACs. The simulator, by emulating $\mathcal {F}_{\textsf{VOLEc}}^{N, \zeta }$ hybrid for G$^*$, can extract them trivially as the hiding property of the IT-MAC no longer holds. See  our full version for a formal captured leakage predicate using a family of wrapper functions.

Simulatable E’s View. To ensure that our protocol preserves security for the semi-honest E, we need to construct a simulator to sample the entire views of E from knowing the computation result. This can be easily reduced to the security of BLLL’s GC and SHVZK property of the parallel SP $\varSigma$-protocol. Informally, the simulator can first use the simulator of BLLL’s GC to generate fake garbled tables and fake garbled labels, then call the simulator of SHVZK to generate the fake proofs. By knowing the global key $\varDelta$, the simulator can easily open an IT-MACs commitment to any value and perform wrong multiplication operations. Formally, the security claims of our protocols are provided in Theorems 3 and 4. The overall efficiency analysis of our protocol is discussed in Sect. 1.2, where a detailed cost accounting is included in our full version.

Lemma 4

(Correct Execution). For every protocol execution between an adversary G$^*$ and E, as defined in our full version Figs. 5, 6a and 6b, such that E outputs $res$ (embedded into $\mathbb {Z}_{N^\zeta }$), there exists a well defined $\widetilde{\boldsymbol{x}}$ that correspond to the committed values in Step 4, and $\boldsymbol{y}$ that denote E’s inputs, such that $res = \mathcal {C} (\widetilde{\boldsymbol{x}}, \boldsymbol{y})$ with overwhelming probability.

Theorem 3

(Malicious G). Let $\textsf{pp}$ denote the public parameters for any circuit $\mathcal {C}$ defined over B-bounded integer computations. Then protocol $\mathrm {\Pi }$ specified in our full version and Figs. 5, 6a and 6b securely computes $\mathcal {C}$ (embedded within $\mathbb {Z}_{N^\zeta }$) with 1-bit leakage in the presence of malicious G in the $\{\mathcal {F}_{\textsf{VOLEc}}^{N, \zeta },\mathcal {F}_{\textsf{aVOLE}}^{N, \zeta }\}$-hybrid model, where the leakage predicate is defined by the wrapper function $\textsf{Wrap}^{\textsf{pp},\mathcal {C}}$ specified in  our full version.

Theorem 4

(Semi-honest E). Let $\textsf{pp}$ denote that public parameters, for any circuit $\mathcal {C}$ defined over B-bounded integer computations and assume the DCR assumption. Then protocol $\mathrm {\Pi }$ specified in our full version Figs. 5, 6a and 6b securely computes $\mathcal {C}$ (embedded within $\mathbb {Z}_{N^\zeta }$) in the presence of semi-honest E in the $\{\mathcal {F}_{\textsf{VOLEc}}^{N, \zeta },\mathcal {F}_{\textsf{aVOLE}}^{N, \zeta }\}$-hybrid model.