Abstract
Partially Oblivious Pseudorandom Functions (POPRFs) are 2-party protocols that allow a client to learn pseudorandom function (PRF) evaluations on inputs of its choice from a server. The client submits two inputs, one public and one private. The security properties ensure that the server cannot learn the private input, and the client cannot learn more than one evaluation per POPRF query. POPRFs have many applications including password-based key exchange and privacy-preserving authentication mechanisms. However, most constructions are based on classical assumptions, and those with post-quantum security suffer from large efficiency drawbacks.
In this work, we construct a novel POPRF from lattice assumptions and the “Crypto Dark Matter” PRF candidate (TCC’18) in the random oracle model. At a conceptual level, our scheme exploits the alignment of this family of PRF candidates, relying on mixed modulus computations, and programmable bootstrapping in the torus fully homomorphic encryption scheme (TFHE). We show that our construction achieves malicious client security based on circuit-private FHE, and client privacy from the semantic security of the FHE scheme. We further explore a heuristic approach to extend our scheme to support verifiability, based on the difficulty of computing cheating circuits in low depth. This would yield a verifiable (P)OPRF. We provide a proof-of-concept implementation and preliminary benchmarks of our construction. For the core online OPRF functionality, we require amortised 10.0 KB communication per evaluation and a one-time per-client setup communication of 2.5 MB.
You have full access to this open access chapter, Download conference paper PDF
Keywords
1 Introduction
Oblivious pseudorandom functions allow two parties to compute a pseudorandom function (PRF) \(z :=F_k(x)\) together: a server supplying a key \(k\) and a user supplying a private input \(x\). The server does not learn \(x\) or \(z\) and the user does not learn \(k\). If the user can be convinced that \(z\) is correct (i.e. that evaluation is performed under the correct key) then the function is “verifiable oblivious” (VOPRF), otherwise it is only “oblivious” (OPRF). Both may be used in many cryptographic applications. Example applications include anonymous credentials (e.g. Cloudflare’s PrivacyPass [22]) and Private Set Intersection (PSI) enabling e.g. privacy-preserving contact look-up on chat platforms [18].
The obliviousness property can be too strong in many applications where it is sufficient or even necessary to only hide part of the client’s input. In this case, the public and private inputs are separated by requiring an additional public input t, called the tag. Then we say that we have a Partially Oblivious PRF (POPRF). POPRFs are typically used in protocols where a server may wish to rate-limit OPRF evaluations made by a client. Such example protocols include Password-Authenticated Key Exchanges (e.g. OPAQUE [37], which is in the process of Internet Engineering Task Force (IETF) standardisation) and the Pythia PRF service [27]. This latter work also proposed a bilinear pairing-based construction of a Verifiable POPRF (VPOPRF), which is the natural inclusion of both properties: some of the input is revealed to the server and the client is able to check the correct evaluation of its full input.
Despite the wide use of (VP)OPRFs, most constructions are based on classical assumptions, such as Diffie-Hellman (DH), RSA or even pairing-based assumptions. The latest in this line of research is a recent VPOPRF construction based on a novel DH-like assumption [51] and DH-based OPRFs are currently being standardised by the IETF. Their vulnerability to quantum adversaries makes it desirable to find post-quantum solutions, however, known candidates are much less efficient.
Given fully homomorphic encryption (FHE), there is a natural (P)OPRF candidate. The client FHE encrypts input \(x\) and sends it with tag \(t\). The server then evaluates the PRF homomorphically or “blindly” using a key derived from \(t\) and its own secret key. Finally, the client decrypts the resulting ciphertext to obtain the PRF output. The first challenge with this approach is performance – PRFs tend to have sufficiently deep circuits that FHE schemes struggle to evaluate them efficiently. Even special purpose PRFs such as the LowMC construction [5] require depth ten or more, making them somewhat impractical. More generally, in a binary circuit model we expect to require depth \(\Theta ( \log \lambda )\) to obtain a PRF resisting attacks with complexity \(2^{\Theta (\lambda )}\).
Yet, if we expand our circuit model to arithmetic circuits with both mod \(p\) and mod \(q\) gates for \(p\ne q\) both primes, shallow proposals exist [11, 23]. In particular, the (weak) PRF candidate in [11] is
where arithmetic operations are over the integers and \(\boldsymbol{A} \) is the secret key. The same work also contains a proposal to “upgrade” this weak PRF, defined for uniformly random inputs \(\boldsymbol{x} \), to a full PRF, taking any \(\boldsymbol{x} \). Furthermore, the works [11, 23] already provide oblivious PRF candidates based on this PRF and MPC, but with non-optimal round complexity. Thus, a natural question to ask is if we can construct a round-optimal (or, 2 message) POPRF based on this PRF candidate using the FHE-based paradigm mentioned above.
1.1 Contributions
Our starting point is the observation that the computational model in [11] aligns well with that of the TFHE encryption scheme [21] and its “programmable bootstrapping” technique [38, 46]. Programmable bootstrapping allows us to realise arbitrary, not necessarily low-degree, small look-up tables and thus function evaluations on (natively) single inputs. Thus, it is well positioned to realise the required gates.Footnote 1 Indeed, FHE schemes natively compute plaintexts modulo some \(P \in \mathbb {Z}\) and we observe that programmable bootstrapping allows us to switch between these plaintext moduli, e.g. from mod \(P_{1}\) to mod \(P_{2}\). This implies a weak PRF with a single level of bootstrapping only. We believe this simple observation and conceptual contribution will have applications beyond this work. We further hope that by giving another application domain for the PRF candidate from [11] – it is not just MPC-friendly but also (T)FHE-friendly – we encourage further cryptanalysis of it.
After some preliminaries in Sect. 2 we specify our POPRF candidate in Sect. 3 based on programmable bootstrapping for plaintext modulus switching. In particular, we define an operation called \(\textsf{CPPBS}_{(2,3)}\) which uses a programmable bootstrap with a special negacyclic “test polynomial” and a simple linear function to “correct” and realise the desired modulus switch. To our knowledge this functionality has not been explicitly defined and used in prior work. Without the bespoke design of \(\textsf{CPPBS}_{(2,3)}\), we are forced to either use only half of the plaintext space, or use a sequence of two programmable bootstraps [42]. The former drawback prevents bootstrapping-less homomorphic addition modulo \(P_1\), whereas the latter does not permit a depth one bootstrapping construction.
As is typical with FHE-based schemes, we require the involved parties – here the client – to prove that its inputs are well-formed. We also make use of the protected encoded-input PRF (PEI-PRF) paradigm from [11]. In particular, the client performs some computations not dependent on secret key material and then submits the output together with a NIZK proof of well-formedness to the server for processing.
We prove our construction secure in the random oracle model in Sect. 4. We show that our construction meets the security definitions from [51]: pseudorandomness even in the presence of malicious clients (POPRF security) and privacy for clients. This property has two flavours based on the capabilities of the adversary, POPRIV1 (which we achieve) captures security against an honest-but-curious server, whereas POPRIV2 ensures security even when the server is malicious. Here, the client maintains privacy by detecting malicious behaviour of the server. POPRF security for the server essentially rests on circuit-privacy obtained from TFHE bootstrapping [40] and a client NIZK. The NIZK is made online extractable in the POPRF proof using a trapdoor and thus avoids any rewinding issues outlined in e.g. [49], and similarly mitigates the problem of rewinding for post-quantum security, cf. [52]. POPRIV1 security for the client against a semi-honest server relies on the IND-CPA security of TFHE.
Targeting roughly 100 bits of security, we obtain the following performance. While the public key material sent by the client to the server is large (14.7 MB) this cost can be amortised by reusing the same material for several evaluations. Individual PRF evaluations can then cost about 48.9 KB or as little as 5.3 KB when amortising client NIZK proofs across several OPRF queries. Applying the public-key compression technique of [39], we obtain 2.5 MB of public-key material at the cost of increasing the amortised cost to 10.0 KB (see Table 1).
Initially, we focus on oblivious rather than verifiable oblivious PRFs. This is motivated by the presumed high cost associated with zero-knowledge proofs for performing FHE computations. In Sect. 5, we explore a different approach to adding verifiability to our OPRF, inspired by and based on a discussion in [2]. The idea here is that the server commits to a set of evaluation “check” points and that the client can use the oblivious nature of the PRF to request PRF evaluations of these points to catch a cheating server. However, achieving security of this “cut-and-choose” approach in our setting is non-trivial as the server may still obliviously run a cheating circuit that agrees on those check points but diverges elsewhere.
We explore the feasibility of such a cheating circuit using direct cryptanalysis. Inspired by the heuristic approach in [18] for achieving malicious security – forcing the server to compute a deep circuit in FHE parameters supporting only shallow circuits – we explore cheating circuits in bootstrapping depth one. While we were unable to find such a cheating circuit, and conjecture that none exists, we stress that this part of our work is highly speculative. Note that the assumption here depends on the bootstrapping depth of the OPRF, i.e. if depth \(d>1\) was required for OPRF evaluation, the assumption would need to be that there is no cheating circuit in depth \(d\). Therefore, our depth one construction leads to an “optimal” assumption for the cut-and-choose method. Under the heuristic assumption that our construction is verifiable, in Sect. 5.3 we then establish that it also satisfies POPRIV2. We hope that our work encourages further exploration of such strategies, as these will have applications elsewhere to upgrade FHE-based schemes to malicious security and OPRFs to VOPRFs.
We present a proof-of-concept SageMath implementation and some indicative Rust benchmarks in Sect. 6. Our SageMath implementation covers all building blocks except for the zero-knowledge proofs, which we consider out of scope. In particular, we re-implemented TFHE [21], including circuit privacy [40] and ciphertext and public-key compression [17, 39]. Our Rust benchmarks make use of Zama’s tfhe-rs library for implementing TFHE, which – however – does not implement many of the building blocks we make use ofFootnote 2 and thus mostly serves as an initial, best-case performance evaluation. In particular, we expect circuit privacy and public-key compression to increase the runtime by a factor of, say, ten (we discuss this Sect. 6). We also did not implement the NIZKs in Rust. With these caveats in mind, the client online functions we could implement run in 28.9 ms on one core and server online functions run in 151 ms on 64 cores.
In the full version [1], we also estimate costs of the required non-interactive zero-knowledge proofs. We use a combination of [44] and [10] to show that the cost of the proofs does not add significant overhead to the communication of our protocol.
1.2 Related Work
Oblivious PRFs and variants thereof are an active area of research. A survey of constructions, variants and applications was given in [16]. In this work we are interested in plausibly post-quantum and round-optimal constructions. The first construction was given in [2], which built a verifiable oblivious PRF from lattice assumptions following the blueprint of Diffie-Hellman constructions with additive blinding (a construction for multiplicative blinding is given in an appendix of the full version of [2]). The work provides both semi-honest and malicious secure candidates with the latter being significantly more expensive. We stress that in the former, both parties are semi-honest.
In [12] two candidate constructions from isogenies were proposed. One, a VOPRF related to SIDH, was unfortunately shown to not be secure [7]. The other, an OPRF related to CSIDH, achieves sub megabyte communication in a malicious setting assuming the security of group-action decisional Diffie-Hellman. In [6] a fixed-and-improved SIDH-based candidate was proposed and in [34] an improved CSIDH-based candidate is presented, both of which rely on trusted setups. In [48] an OPRF based on the Legendre PRF is proposed based on solving sparse multi-variate quadratic systems of equations. In [23], which also builds on [11], an MPC-based OPRF is proposed that is secure against semi-honest adversaries. It achieves much smaller communication complexity compared to all other post-quantum candidates, but in a preprocessing model where correlated randomness is available to the parties. A protocol computing this correlated randomness, e.g. [14], would add two rounds (or more) and thus make the overall protocol not round-optimal. The question of upgrading security to full malicious security is left as an open problem in [23]. In [28] a generic MPC solution not relying on novel assumptions is proposed, that, while not round-optimal, reportedly provides good performance in various settings.
We give a summary comparison of our construction with prior work in Table 1. The only 2-round constructions without preprocessing or trusted-setup in Table 1 are those from [2], where our construction compares favourably by offering stronger claimed qualitative security at smaller size, albeit under novel assumptions. In particular, even in a semi-honest setting, our construction outperforms that from [2] in terms of bandwidth for \(L \ge 2\) queries.Footnote 3
1.3 Open Problems
A pressing open problem is to refine our understanding of the security of the PRF candidate from [11]. In particular, our parameter choices may prove to be too aggressive, and we hope that our work inspires cryptanalysis.
A key bottleneck for implementations will be bootstrapping, an effect that will exacerbated by the need for circuit-private bootstrapping. It is an open problem to establish if this somewhat heavy machinery is required given that we are only aiming to hide the secret key \(\boldsymbol{A} \) and that we can randomise our circuit by randomly flipping signs in the additions induced by \(\boldsymbol{A} \).
Considering Table 1, we note that many candidates forgo round-optimality to achieve acceptable performance. It is an interesting open question how critical this requirement is for various applications, since dropping it seems to enable significantly more efficient post-quantum instantiations of (V)OPRFs.
Our verifiability approach throws up a range of interesting avenues to explore for VOPRFs but also for verifiable homomorphic computation, more generally. First, our OPRF construction relies on programmable bootstrapping. This restricts the choice of FHE scheme we might instantiate our protocol with, but also gives the server the choice which function to evaluate, something our application does not require. That is, we may not need to rely on evaluator programmable bootstrapping if it is possible for the client to define the non-linear functions available to a server (encrypter programmable bootstrapping). This would enable to reason about malicious server security more easily.
Related works, e.g. [18], have also used similar assumptions as our work over the hardness of computing deep circuits in low FHE depth. There is growing evidence that such assumptions allow for new, interesting or more efficient constructions of cryptographic primitives. However, the hardness of these computational problems needs to be better understood.
Finally, our VOPRF is even more speculative than our OPRF candidate. A more direct approach would be to construct a NIZK for correct bootstrapping evaluation, which would have applications beyond this work.
2 Preliminaries
We use \(\lfloor \cdot \rfloor , \lceil \cdot \rceil \) and \(\lfloor \cdot \rceil \) to denote the standard floor, ceiling and rounding to the nearest integer functions (rounding down in the case of a tie). We denote the integers by \(\mathbb {Z}\) and for any positive \(p \in \mathbb {Z}\), the integers modulo \(p\) are denoted by \(\mathbb {Z}_p\). We typically use representatives of \(\mathbb {Z}_p\) in \(\{-p/2, \dots , (p/2) -1 \}\) if \(p\) is even and \(\{-\lfloor p/2 \rfloor , \dots , \lfloor p/2 \rfloor \}\) if \(p\) is odd, but we will also consider \(\mathbb {Z}_{p}\) as \(\{0,1,\ldots ,p-1\}\). Since it will always be clear from context or stated explicitly which representation we use, this does not create ambiguity. The \(p\)-adic decomposition of an integer \(x \ge 0\) is a tuple \({(x_{i})}_{0 \le i < \lceil \log _p(x) \rceil }\) with \(0 \le x_{i} < p\) such that \(x = \sum p^{i} \cdot x_{i}\). We denote the set \(S_m\) to be the permutation group of \(m\) elements.
Let \(\mathbb {Z}[X]\) denote the polynomial ring in the variable \(X\) whose coefficients belong to \(\mathbb {Z}\). We also denote power-of-two cyclotomic rings \(\mathcal {R} :=\mathbb {Z}[X]/(X^d+1)\) where \(d\) is a power-of-two, and \(\mathcal {R} _q :=\mathcal {R}/(q\,\mathcal {R})\) for any integer “modulus” \(q\). Bold letters denote vectors and upper case letters denote matrices. Abusing notation we write \((\boldsymbol{x},\boldsymbol{y})\) for the concatenation of the vectors \(\boldsymbol{x} \) and \(\boldsymbol{y} \). We extend this notation to scalars, too. Additionally, \(\Vert \cdot \Vert \)and \(\Vert \cdot \Vert _\infty \) denote standard Euclidean and infinity norms respectively.
For a distribution \(D\), we write
 to denote that \(x\) is sampled according to the distribution \(D\). An example of a distribution is the discrete Gaussian distribution over \(\mathbb {Z}\) with parameter \(\sigma >0\) denoted as \(D_{\mathbb {Z},\sigma }\). This distribution has its probability mass function proportional to the Gaussian function \(\rho _{\sigma }(x) :=\exp (-\pi x^2/\sigma ^2)\). We use \(\lambda \) to denote the security parameter. We use the standard asymptotic notation (\(\Omega , \mathcal {O}, \omega \) etc.) and use \(\textsf{negl}\left( \lambda \right) \) to denote a negligible function, i.e. a function that is \(\lambda ^{\omega (1)}\). Further, we write \(\textsf{poly}\left( \lambda \right) \) to denote a polynomial function i.e. a function that is \(\mathcal {O}(n^c)\) for some constant \(c\). An algorithm is said to be polynomially bounded if it terminates after \(\textsf{poly}\left( \lambda \right) \) steps and uses \(\textsf{poly}\left( \lambda \right) \)-sized memory. Two distribution ensembles \(D_1(1^{\lambda })\) and \(D_2(1^{\lambda })\) are said to be computationally indistinguishable if for any probabilistic polynomially bounded algorithm \(\mathcal {A}\),
to denote that \(x\) is sampled according to the distribution \(D\). An example of a distribution is the discrete Gaussian distribution over \(\mathbb {Z}\) with parameter \(\sigma >0\) denoted as \(D_{\mathbb {Z},\sigma }\). This distribution has its probability mass function proportional to the Gaussian function \(\rho _{\sigma }(x) :=\exp (-\pi x^2/\sigma ^2)\). We use \(\lambda \) to denote the security parameter. We use the standard asymptotic notation (\(\Omega , \mathcal {O}, \omega \) etc.) and use \(\textsf{negl}\left( \lambda \right) \) to denote a negligible function, i.e. a function that is \(\lambda ^{\omega (1)}\). Further, we write \(\textsf{poly}\left( \lambda \right) \) to denote a polynomial function i.e. a function that is \(\mathcal {O}(n^c)\) for some constant \(c\). An algorithm is said to be polynomially bounded if it terminates after \(\textsf{poly}\left( \lambda \right) \) steps and uses \(\textsf{poly}\left( \lambda \right) \)-sized memory. Two distribution ensembles \(D_1(1^{\lambda })\) and \(D_2(1^{\lambda })\) are said to be computationally indistinguishable if for any probabilistic polynomially bounded algorithm \(\mathcal {A}\),
 . In such a case we write \(D_1(1^\lambda ) \approx _c D_2(1^\lambda )\). The distribution ensembles are said to be statistically indistinguishable if the same holds for all unbounded algorithms, in which case we write \(D_1(1^\lambda ) \approx _s D_2(1^\lambda )\).
. In such a case we write \(D_1(1^\lambda ) \approx _c D_2(1^\lambda )\). The distribution ensembles are said to be statistically indistinguishable if the same holds for all unbounded algorithms, in which case we write \(D_1(1^\lambda ) \approx _s D_2(1^\lambda )\).
For a key space \(\mathcal {K}\), input space \(\mathcal {X}\) and output space \(\mathcal {Z}\), a PRF is a function \(F:\mathcal {K} \times \mathcal {X} \longrightarrow \mathcal {Z} \) with a pseudorandomness property. Rather than writing \(F(k,x)\) for \(k \in \mathcal {K}\) and \(x \in \mathcal {X}\), we write \(F_k(x)\). The pseudorandomness property of a PRF requires that over a secret and random choice of
 , the single input function \(F_k(\cdot )\) is computationally indistinguishable from a uniformly random function. Note here that the dependence of the parameters on \(\lambda \) is present, but is not explicitly written for simplicity. We also use the standard cryptographic notion of a (non-interactive) zero-knowledge proof/argument. For more details on these standard cryptographic notions, see e.g. [33].
, the single input function \(F_k(\cdot )\) is computationally indistinguishable from a uniformly random function. Note here that the dependence of the parameters on \(\lambda \) is present, but is not explicitly written for simplicity. We also use the standard cryptographic notion of a (non-interactive) zero-knowledge proof/argument. For more details on these standard cryptographic notions, see e.g. [33].
2.1 Random Oracle Model
We will prove security by modelling hash functions as random oracles. Since our schemes will make use of more than one hash function, it will be useful to have a general abstraction for the use of ideal primitives, following the treatment in [51]. A random oracle \(\textsf{RO}\) specifies algorithms \(\textsf{RO}.\textsf{Init}\) and \(\textsf{RO}.\textsf{Eval}\). The initialisation algorithm has syntax
 . The stateful evaluation algorithm has syntax
. The stateful evaluation algorithm has syntax
 . We sometimes use \(A^\textsf{RO}\) as shorthand for giving algorithm \(A\) oracle access to \(\textsf{RO}.\textsf{Eval}(\cdot , st_\textsf{RO})\). We combine access to multiple random oracles \(\textsf{RO}= \textsf{RO}_{0} \times \ldots \times \textsf{RO}_{m-1}\) in the obvious way. We may arbitrarily label our random oracles to aid readability e.g. \(\textsf{RO}_{\textsf{key}}\) to denote a random oracle applied to some “key”.
. We sometimes use \(A^\textsf{RO}\) as shorthand for giving algorithm \(A\) oracle access to \(\textsf{RO}.\textsf{Eval}(\cdot , st_\textsf{RO})\). We combine access to multiple random oracles \(\textsf{RO}= \textsf{RO}_{0} \times \ldots \times \textsf{RO}_{m-1}\) in the obvious way. We may arbitrarily label our random oracles to aid readability e.g. \(\textsf{RO}_{\textsf{key}}\) to denote a random oracle applied to some “key”.
2.2 (Verifiable) (Partial) Oblivious Pseudorandom Functions
We adopt the notation and definitions for oblivious pseudorandom functions from [51]. An OPRF is a protocol between two parties: a server \(\textsf{S}\) who holds a private key and a client who wants to obtain evaluations of \(F_k\) on inputs of its choice. We write \(z :=F_{k}(x)\). We say that an OPRF is a partial OPRF (POPRF) if part of the client’s input is given to the server. In this case, we write \(z :=F_{k}(t,x)\) where \(t\) is in the clear and \(x\) is hidden from \(\textsf{S}\). When \(\textsf{C}\) can verify that the PRF was evaluated correctly we speak of a verifiable OPRF (VOPRF) or VPOPRF when the protocol also supports partially known inputs \(t\).
Definition 1
(Partial Oblivious PRF [51]). A partial oblivious PRF (POPRF) \(\mathcal {F}\) is a tuple of PPT algorithms
The setup and key generation algorithm generate public parameter \(\textsf{pp}\) and a public/secret key pair \((\textsf{pk},\textsf{sk})\). Oblivious evaluation is carried out as an interactive protocol between \(\textsf{C}\) and \(\textsf{S}\), here presented as algorithms \(\mathcal {F}.\textsf{Request}\), \(\mathcal {F}.\textsf{BlindEal}\), \(\mathcal {F}.\textsf{Finalise}\) working as follows:
-
1.
First, \(\textsf{C}\) runs the algorithm \(\mathcal {F}.\textsf{Request}_{\textsf{pp}}^{\textsf{RO}}(\textsf{pk}, t, x)\) taking a public key \(\textsf{pk}\), a tag or public input \(t\) and a private input \(x\). It outputs a local state \(st\) and a request message \(req\), which is sent to the server.
-
2.
\(\textsf{S}\) runs \(\mathcal {F}.\textsf{BlindEal}_{\textsf{pp}}^{\textsf{RO}}(\textsf{sk}, t, req)\) taking as input a secret key \(\textsf{sk}\), a tag \(t\) and the request message \(req\). It produces a response message \(rep\) sent back to \(\textsf{C}\).
-
3.
Finally, \(\textsf{C}\) runs \(\mathcal {F}.\textsf{Finalise}(rep, st)\) which takes the response message and its previously constructed state \(st\) and either outputs a PRF evaluation or \(\bot \) if \(rep\) is rejected.
The unblinded evaluation algorithm \(\mathcal {F}.\textsf{Eval}\) is deterministic and takes as input a secret key \(\textsf{sk}\), an input pair \((t,x)\) and outputs a PRF evaluation \(z\).
We also define sets \(\mathcal {F}.\textsf{SK}\), \(\mathcal {F}.\textsf{PK}\), \(\mathcal {F}.\textsf{T}\), \(\mathcal {F}.\textsf{X}\) and \(\mathcal {F}.\textsf{Out}\) representing the secret key, public key, tag, private input, and output space, respectively. We define the input space \(\mathcal {F}.\textsf{In}= \mathcal {F}.\textsf{T}\times \mathcal {F}.\textsf{X}\). We assume efficient algorithms for sampling and membership queries on these sets.
Remark 1
Fixing \(t\), e.g. \(t=\bot \), recovers the definition of an OPRF.
We adapt correctness from [51], permitting a small failure probability.
Definition 2
(POPRF Correctness (adapted from [51])). A partial oblivious PRF (POPRF)
is correct if

We target the same pseudorandomness guarantees against malicious clients as [51].
Definition 3
(Pseudorandomness (POPRF) [51]). We say a partial oblivious PRF \(\mathcal {F}\) is pseudorandom if for all \(\textsf{PPT}\) adversaries \(\mathcal {A}\), there exists a PPT simulator \(\textsf{S}\) such that the following advantage is \(\textsf{negl}\left( \lambda \right) \):
Remark 2
In Fig. 1, the oracle \(\textrm{Prim}(x)\) captures access to the random oracle used in the POPRF construction. For \(b=0\) (the case where the adversary interacts with a simulator and a truly random function) the simulator may only use a limited number of random function queries to simulate the random oracle accessed via \(\textrm{Prim}(x)\).
The intuition of this definition is that it requires the simulator to explain a random output (defined via \(\textsf{RO}_{\textsf{Fn}}\)) as an evaluation point of the PRF. The simulator provides its own public key and public parameters, but it gets at most one query to \(\textsf{RO}_{\textsf{Fn}}()\) per \(\textsf{BlindEal}\) query that it has to simulate. The simulator queries \(\textsf{RO}_{\textsf{Fn}}\) through calls to LimitEval, where the check \(q_{t,s} \le q_t\) enforces the number of queries per \(\textsf{BlindEal}\) query and tag \(t\). This implies that \(\textsf{BlindEal}\) and \(\textsf{Eval}\) queries essentially leak nothing beyond a single evaluation to the client. Moreover, the simulator is restricted in that the LimitEval oracle will error if more queries are made to it than the number of BlindEval queries (on t) at any point in the game. Meaningful relaxations of this definition are discussed in [51], but for completeness we opt for the full definition (Fig. 2).
Definition 4
(Request Privacy (POPRIV) [51]). We say a partial oblivious PRF \(\mathcal {F}\) has request privacy against honest-but-curious and malicious servers respectively if for all \(\textsf{PPT}\) adversary \(\mathcal {A}\) the following advantage is \(\textsf{negl}\left( \lambda \right) \) for \(k=1\) and \(k=2\) respectively:
2.3 Hard Lattice Problems
We will rely on both the \(M\text {-}\textsf{SIS} \) and the \(M\text {-}\textsf{LWE} \) problems. Instantiating these over \(\mathcal {R} =\mathbb {Z}\) recovers the SIS and LWE problems respectively. Further, instantiating these over some ring of integers of some number field and with \(n=1\), recovers the Ring-SIS and Ring-LWE problems respectively.
Definition 5
( \(M\text {-}\textsf{SIS}\) , adapted from [41]). Let \(\mathcal {R},q,n,\ell ,\beta \) depend on \(\lambda \). The Module-SIS (or M-SIS) problem, denoted \(M\text {-}\textsf{SIS}_{\mathcal {R} _q,n,\ell ,\beta ^*} \), is: Given a uniform
 find some \(\boldsymbol{u} \ne \boldsymbol{0} \in \mathcal {R}^\ell \) such that \(\Vert \boldsymbol{u} \Vert \le \beta ^{*}\) and \({\boldsymbol{A}}\cdot {\boldsymbol{u}} \equiv \boldsymbol{0} \bmod q\).
find some \(\boldsymbol{u} \ne \boldsymbol{0} \in \mathcal {R}^\ell \) such that \(\Vert \boldsymbol{u} \Vert \le \beta ^{*}\) and \({\boldsymbol{A}}\cdot {\boldsymbol{u}} \equiv \boldsymbol{0} \bmod q\).
Definition 6
( \(M\text {-}\textsf{LWE}\) , adapted from [41]). Let \(\mathcal {R},q,n,m\) depend on \(\lambda \) and let \(\chi _s,\chi _e\) be distributions over \(\mathcal {R} _q\). Denote by \(M\text {-}\textsf{LWE}_{\mathcal {R} _q,n,\chi _s,\chi _e} \) the probability distribution on \(\mathcal {R} _q^{m \times n}\times \mathcal {R} _q^m\) obtained by sampling the coordinates of the matrix \(\boldsymbol{A} \in \mathcal {R} _q^{m \times n}\) independently and uniformly over \(\mathcal {R} _q\), sampling the coordinates of \(\boldsymbol{s} \in \mathcal {R} _q^n\), \(\boldsymbol{e} \in \mathcal {R} ^m\) independently from \(\chi _s\) and \(\chi _e\) respectively, setting \(\boldsymbol{b} :=\boldsymbol{A} \cdot \boldsymbol{s} +\boldsymbol{e} \bmod q\) and outputting \((\boldsymbol{A},\boldsymbol{b})\). The \(M\text {-}\textsf{LWE}\) problem is to distinguish the uniform distribution over \(\mathcal {R} _q^{m\times n}\times \mathcal {R} _q^m\) from \(M\text {-}\textsf{LWE}_{\mathcal {R} _q,n,\chi _s,\chi _e} \).
2.4 Matrix NTRU Trapdoors
The original formulation [35] of the NTRU problem considers rings of integers of number fields or polynomial rings, but a matrix version is implicit and considered for cryptanalysis in the literature.
Definition 7
Given integers \(n,p,q,\beta \) where \(p\) and \(q\) are coprime, the matrix-NTRU assumption (denoted \(\textsf{mat}\text {-}\textsf{NTRU}_{n,p,q,\beta }\)) states that no PPT algorithm can distinguish between \(\boldsymbol{A} \) and \(\boldsymbol{B} \) where
-
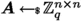
-
\(\boldsymbol{B} = p^{-1} \cdot \boldsymbol{G} ^{-1} \cdot \boldsymbol{F} \mod q\) with
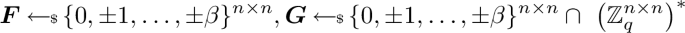
where \({\left( \mathbb {Z}_q^{n \times n}\right) }^*\) denotes the set of invertible \((n \times n)\) matrices over \(\mathbb {Z}_q\).
We will use the matrix-NTRU assumption to define a trapdoor. In what follows, we assume an odd \(q\) and an even \(p\) that is coprime to \(q\). In particular, we define the following algorithms:
- \(\textsf{NTRUTrapGen}(n,q,p,\beta )\)::
-
Sample
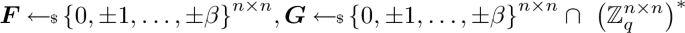
and output public information \( \textsf{pp}:=(p^{-1} \cdot \boldsymbol{G} ^{-1} \cdot \boldsymbol{F} \bmod q, q)\) and a trapdoor \(\tau :=(\boldsymbol{F}, \boldsymbol{G},p)\).
- \(\textsf{NTRUDec}(\boldsymbol{c}, \tau )\)::
-
For \(\boldsymbol{c} \in \mathbb {Z}_q^n\), \(\tau :=(\boldsymbol{F}, \boldsymbol{G}, p)\), compute \(\boldsymbol{c} _1 = p\cdot \boldsymbol{G} \cdot \boldsymbol{c} \bmod q\), \(\boldsymbol{c} _2 = \boldsymbol{c} _1 \bmod (p/2)\), \(\boldsymbol{c} _3 = \boldsymbol{c} - p^{-1}\cdot \boldsymbol{G} ^{-1}\cdot \boldsymbol{c} _2 \bmod q\). Finally, compute and output \(\boldsymbol{m} ' :=\left\lfloor {\frac{2}{q-1} \cdot \boldsymbol{c} _3}\right\rceil \) where the multiplication and rounding is done over the rationals.
The trapdoor functionality is summarised in the lemma below.
Lemma 1
Suppose that \(p,q\) are coprime where \(p\) is even and \(q\) is odd. Suppose also that \(\beta \cdot \beta '_s \cdot n < p/4\), and that \(\beta '_s, \beta '_e \in \mathbb {R}\) satisfies \(\beta \cdot n\cdot (\beta '_s+p\cdot (2\,\beta '_e+1)/2) < q/2\). Sample
 . Then:
. Then:
-
1.
\(\boldsymbol{B} \) is indistinguishable from uniform over \(\mathbb {Z}_q^{n \times n}\) if the \(\textsf{mat}\text {-}\textsf{NTRU}_{n,p,q,\beta }\) assumption holds.
-
2.
If \(\boldsymbol{c} = \boldsymbol{B} \cdot \boldsymbol{s} + \boldsymbol{e} + \lfloor q/2 \rceil \cdot \boldsymbol{m} \bmod q\) where \(\boldsymbol{m} \in \mathbb {Z}_2^n\), \(\left( \Vert \boldsymbol{s} \Vert _{\infty } \le \beta '_s \vee \Vert \boldsymbol{s} \Vert _2 \le \beta '_s \cdot \sqrt{n}\right) \) and \(\left( \Vert \boldsymbol{e} \Vert _\infty \le \beta '_e \vee \Vert \boldsymbol{e} \Vert _2 \le \beta '_e \cdot \sqrt{n}\right) \), then \(\textsf{NTRUDec}(\boldsymbol{c}, \tau ) = \boldsymbol{m} \).
Proof
For the first part, simply note that distinguishing \(\boldsymbol{B} \) from uniform is exactly the matrix-NTRU problem for \((n,p,q,\beta )\). For the second part, reusing the same notation from the description of \(\textsf{NTRUDec}(\boldsymbol{c}, \tau :=(\boldsymbol{F}, \boldsymbol{G}, p))\) gives
over \(\mathbb {Z}\) because \(\Vert \boldsymbol{F} \cdot \boldsymbol{s} + (p/2)\cdot \boldsymbol{G} \cdot (2\,\boldsymbol{e}-\boldsymbol{m})\Vert _{\infty } < q/2\). We then have \(\boldsymbol{c} _2 = \boldsymbol{F} \cdot \boldsymbol{s} \bmod p/2 = \boldsymbol{F} \cdot \boldsymbol{s} \) over \(\mathbb {Z}\) because \(\Vert \boldsymbol{F} \cdot \boldsymbol{s} \Vert _{\infty } < p/4\). Next, \(\boldsymbol{c} _3 = \boldsymbol{e} + ((q-1)/2) \cdot \boldsymbol{m} \). Note that the conditions in the lemma statement imply that \(2\,\beta '_e \cdot \sqrt{n}< (q-1)/2\). This gives the final output \(\lfloor \boldsymbol{m} + \frac{2}{q-1}\cdot \boldsymbol{e} \rceil = \boldsymbol{m} \) because \(\Vert \frac{2\boldsymbol{e}}{q-1}\Vert _\infty < 1/2\). \(\square \)
Choosing Parameters. Looking ahead, we will instantiate this trapdoor for \(q\approx 2^{32}\) and \(n=2^{11}\). So, we require \(\beta \cdot \beta _{s}' < p/(4\,n)\) and, say, \(\beta \cdot \beta '_e < q/(4\,n\cdot p)\). Picking \(p = 2^{16}\), we get \(\log (\beta ) + \log (\beta '_s) < 16 - 2 - 11 = 3\) and \(\log (\beta ) + \log (\beta '_e) < 32-2-11-16 = 3\). Picking \(\beta \approx 2^{2}\) and \(\beta '_{s} = \beta '_{e} \approx 2\) we obtain an NTRU instance requiring BKZ block size 333 to solve (using the (overstretched) NTRU estimator [26]) and an LWE instance requiring BKZ block size 594 to solve (using the lattice estimator [4]). According to the cost model from [45] this costs about \(2^{132}\) classical operations.Footnote 4
2.5 Homomorphic Encryption and TFHE
Fully homomorphic encryption (FHE) allows to perform computations on plaintexts by performing operations on ciphertexts. In slightly more detail, an FHE scheme consists of four algorithms: \(\textsf {FHE}.\textsf{KeyGen}, \textsf {FHE}.\textsf{Enc}, \textsf {FHE}.\textsf{Eval}, \textsf {FHE}.\textsf{Dec}\). The key generation, encryption and decryption algorithms all work similarly to normal public key encryption. Together, they provide privacy (i.e. IND-CPA security) and decryption correctness. The interesting part of FHE is its homomorphic property. Assume that \(\mathcal {M}\) is the message space, e.g. \(\mathcal {M} :=\mathbb {Z}_{P}\). The homomorphic property is enabled by the \(\textsf {FHE}.\textsf{Eval}\) function which takes as input a public key \(\textsf{pk}\), an arbitrary function \(f: \mathcal {M}^{k} \longrightarrow \mathcal {M}\), a sequence of ciphertexts \((c_i)_{i \in [\mathbb {Z}_k]}\) encrypting plaintexts \({(m_i)}_{i \in \mathbb {Z}_k}\), and outputs a ciphertext \(c' \leftarrow \textsf {FHE}.\textsf{Eval}(\textsf{pk}, f, (c_0, \dots ,c_{k-1}))\). The homomorphic property ensures that \(c'\) is an encryption of \(f(m_0, \dots , m_{k-1})\). Intuitively, FHE allows arbitrary computation on encrypted data without having to decrypt. Importantly, the privacy of the plaintext is maintained. In addition, an FHE scheme may also maintain the privacy of the evaluated computation (see below).
FHE was first realised by Gentry [31]. A considerable amount of influential follow-up research provides the basis of most practically feasible schemes [15, 20, 29, 32]. We will be focusing on an extension of the third of these works known as TFHE [21] because its programmable bootstrapping technique lends enables our construction. For a summary of TFHE, see the guide [38].
Programmable Bootstrapping. A crucial ingredient of any FHE scheme is a bootstrapping procedure. Essentially, homomorphic evaluation increases ciphertext noise, meaning that after a prescribed number of evaluations, a ciphertext becomes so noisy that it cannot be decrypted correctly. Bootstrapping provides a method of resetting the size of the noise in a ciphertext to allow for correct decryption using some bootstrapping key material. Note that the bootstrapping operation can either produce a ciphertext encrypted under the original key or a new one depending on the bootstrapping key material used.Footnote 5 We also note that the FHE schemes considered in this work are additively homomorphic with very modest noise growth, meaning that many additions of plaintexts can be performed without bootstrapping.
In TFHE we have access to negacyclic look-up tables from \(\mathbb {Z}_{2d}\) to \(\mathbb {Z}_{P}\) which we will denote by \(f(\cdot ): \mathbb {Z}_{2d} \rightarrow \mathcal {M}\). Here, d is the degree of a cyclotomic ring \(\mathcal {R} = \mathbb {Z}[X]/(X^d+1)\) and \(\mathbb {Z}_P\) is the plaintext space. There is a slight problem here in that the look-up table does not take plaintext-space inputs, but this is overcome by approximating \(\mathbb {Z}_{2d}\) as \(\mathbb {Z}_P\) [21, 38]. TFHE generalises bootstrapping by applying the look-up table to the plaintext at the same time as resetting the size of the noise. The negacyclic property dictates that \(f(x+d)=-f(x)\) for \(x = 0,1,\dots ,d-1\), so if the desired look-up table is not negacyclic, one must either restrict to using half the plaintext space or use more complex bootstrapping techniques [42].
2.6 Circuit Private (Programmable) Bootstrapping
Circuit private FHE hides the computation performed on a ciphertext. There are generic methods of achieving circuit privacy [25] and more specific ones for GSW [13] and TFHE [40]. As our OPRF is designed within the specific framework of TFHE, we restrict discussion to the latter work. At a high level, TFHE bootstrapping consists of two steps: blind rotation and key-switching. Blind Rotation is a Generalised GSW [32] based operation that outputs an LWE ciphertext under a different key. The key-switching phase then maps back to the original key to allow for further homomorphic operations. A key contribution of Kluczniak [40] is a generalised Gaussian leftover hash lemma that shows how to randomise the blind rotation phase in order to “clean up” the noise distribution. Ultimately, this entails adding Gaussian preimage sampling to the blind rotation algorithm which affects computation time and correctness parameters. We note that we will not require key-switching (line 1 of Fig. 3 in [40]), but this does not affect the statistical distance result below in any way. We avoid giving too many details on the meaning of parameters with respect to the circuit privacy bootstrapping algorithm and refer to [40] for details. In the statement below, \(\Vert \boldsymbol{B} _{L,Q}\Vert \) denotes the maximum length of a column of
where \(\ell :=\lceil \log _L(Q)\rceil \) and \((Q_1, \dots , Q_\ell )\) is a base-\(L\) decomposition of \(Q\). We recall the main circuit privacy result from [40] we will use below.
Theorem 1
([40]). Let \(\beta _{\textsf{br}}, \beta _R\) be noise bounds on a blind rotation key and LWE public key respectively and let \(\boldsymbol{c} \) be an input LWE ciphertext with secret \(\boldsymbol{s} \in \mathbb {Z}_2^{n}\). Furthermore, assume the use of a test polynomial \(v(X)\) such that the constant of \(v(X) \cdot X^{\mathsf {Phase(\boldsymbol{c})}}\) is \(f(m)\). Then if
and
then
where \(\boldsymbol{c} _{\textsf{out}}\) is the output of the algorithm in Fig. 3 of [40] and \(\boldsymbol{c} _{\textsf{fresh}} = (\boldsymbol{a} _{\textsf{fresh}}, \boldsymbol{a} _{\textsf{fresh}} \cdot \boldsymbol{s} + f(m) + e_\textsf{rand} + e_{\textsf{out}})\) is a well distributed fresh ciphertext with noise distributions
 ,
,
 .
.
Malicious Security. Note that the definition above is required to hold for “any” \(\textsf {FHE}.\textsf{pk},\textsf {FHE}.\textsf{sk}, \textsf{ct}_{\textsf{out}}\) generated honestly. More precisely, this means for any possible (i.e. valid) outputs of the appropriate \(\textsf {FHE}\) algorithms. For example, the word “any” for an error term distributed as a discrete Gaussian would mean any value satisfying some appropriate bound. Intuitively, malicious circuit privacy requires that an adversary cannot learn anything about the circuit (or \((\boldsymbol{A},\boldsymbol{x})\)) even in the presence of maliciously generated keys and ciphertexts. Thus if we can ensure the well-formedness of keys and ciphertexts, then a semi-honest circuit-private FHE scheme is also secure against malicious adversaries. In the random oracle model, we can achieve this with NIZKs that show well-formedness of the keys and that the ciphertext is a valid ciphertext under that public key. Then, \(\textsf {FHE}\).\(\textsf{Eval}\) can explicitly check that the proof verifies and abort otherwise.
2.7 Crypto Dark Matter PRF
Let \(p,q\) be two primes where \(p < q\). We now describe the “Crypto Dark Matter” PRF candidate [11, 23]. It is built from the following weak PRF proposal \(F_{\textsf{weak}}: \mathbb {Z}_p^{m_{p} \times n_{p}} \times \mathbb {Z}_{p}^{n_p} \rightarrow \mathbb {Z}_q\) where
Here \( \boldsymbol{A} \) is the secret key, \( \boldsymbol{x} \) is the input and \({(\boldsymbol{A} \cdot \boldsymbol{x} \bmod p)}_j\) denotes the j-th component of \( \boldsymbol{A} \cdot \boldsymbol{x} \bmod p\). In order to describe the strong PRF construction, we introduce a fixed public matrix \( \boldsymbol{G} _{\textsf{inp}}\in \mathbb {Z}_q^{n_{q} \times n} \) and a \(p\)-adic decomposition operation \( \textsf{decomp}: \mathbb {Z}_q^{n_q} \rightarrow \mathbb {Z}_p^{\lceil \log _{p}(q) \rceil \cdot n_q} \) where \(\lceil \log _{p}(q) \rceil \cdot n_q = n_{p}\). The strong PRF candidateFootnote 6 is \(F_{\textsf{one}}: \mathbb {Z}_p^{m_{p} \times n_{p}} \times \mathbb {Z}_p^{n} \rightarrow \mathbb {Z}_q\) where
In order to extend the small output of the above PRF constructions, the authors of [11] introduce another matrix \(\boldsymbol{G} _{\textsf{out}}\in \mathbb {Z}_q^{m \times m_p}\) (with \(m < m_{p}\)) which is the generating matrix of some linear code. Then the full PRF is \( F_\textsf{strong}: \mathbb {Z}_p^{m_{p} \times n_p} \times \mathbb {Z}_p^n \rightarrow \mathbb {Z}_q^m \) where
Given access to gates implementing mod \(p\) and mod \(q\) this PRF candidate can be implemented in a depth 3 arithmetic circuit. See the full version [1] for an example implementation, or the attachment.Footnote 7
Note that \(\textsf{decomp}(\boldsymbol{G} _{\textsf{inp}}\cdot \boldsymbol{x} \bmod q) \in \mathbb {Z}_{p}^{n_p}\) does not depend on the PRF key. Thus, in an OPRF construction it could be precomputed and submitted by the client knowing \(\boldsymbol{x} \). However, in this case, we must enforce that the client is doing this honestly via a zero-knowledge proof \(\pi \) that \(\boldsymbol{y} :=\textsf{decomp}(\boldsymbol{G} _{\textsf{inp}}\cdot \boldsymbol{x} \bmod q)\) is well-formed. Specifically, following [11], if \(\boldsymbol{H} _{\textsf{inp}}\in \mathbb {Z}_{q}^{(n_q -n) \times n_q}\) is the parity check matrix of \(\boldsymbol{G} _{\textsf{inp}}\) and \(\boldsymbol{G} _{\textsf{gadget}}:=(p^{\lceil \log _p(q) \rceil - 1}, \ldots , 1) \otimes \boldsymbol{I} _{n_p}\) we may check
Note that as stated this does not enforce \(\boldsymbol{x} \in \mathbb {Z}_{p}^{n}\) but \(\boldsymbol{x} \in \mathbb {Z}_{q}^{n}\). Since it is unclear if this has a security implication, we may avoid this issue relying on a comment made in [11] that we may, wlog, replace \(\boldsymbol{G} _{\textsf{inp}}\) with a matrix in systematic (or row echelon) form. That is, writing \(\boldsymbol{G} _{\textsf{inp}}= {[\boldsymbol{I} \mid \boldsymbol{A} ]}^{T} \in \mathbb {Z}_{q}^{n_p \times n}\), \(\boldsymbol{y} = (\boldsymbol{y} _0, \boldsymbol{y} _1) \in \mathbb {Z}_{q}^{n_p}\), the protected encoded-input PRF is defined as
Note that with this definition of \(\boldsymbol{G} _{\textsf{inp}}\) the “most significant bits” of \(\boldsymbol{y} _{0}\) will always be zero, so there is no point in extracting those when running \(\textsf{decomp}\). Thus, we adapt \(\textsf{decomp}\) to simply return the first \(n\) output values in \(\{0,1\}\) and to perform the full decomposition on the remaining \((n_{q}-n)\) entries. We thus obtain \(n_{p} :=n + \lceil \log _{p}(q) \rceil \cdot (n_q-n)\). A similar strategy is discussed in Remark 7.13 of the full version of [11] (Table 2).
Security Analysis. The initial work [11] provided some initial cryptanalysis and relations to known hard problems to substantiate the security claims made therein. When \(\boldsymbol{A} \) is chosen to be a circulant rather than a random matrix, the scheme has been shown to have degraded security [19] contrary to the expectation stated in [11]. The same work [19] also proposes a fix. Further cryptanalysis was preformed in [23], supporting the initial claims of concrete security. Our choices for \(\lambda = 128\) (classically) are aggressive, especially for a post-quantum construction. This is, on the one hand, to encourage cryptanalysis. On the other hand, known cryptanalytic algorithms against the proposals in [11, 23] require exponential memory in addition to exponential time, a setting where Grover-like square-root speed-ups are less plausible, cf. [3] (which, however, treats the Euclidean distance rather than Hamming distance).
3 Boostrapping Depth One OPRF Candidate
We wish to design an (P)OPRF where the server homomorphically evaluates the PRF using its secret key and uses some form of circuit-private homomorphic encryption to protect its key. The depth of bootstrapping required is one, which enhances efficiency and is useful in the security of our V(P)OPRF in Sect. 5.
3.1 Extending the PEI PRF
Here, we first note that the PRFs defined in Sect. 2.7 trivially fail to achieve pseudorandomness as they map \(\boldsymbol{0} \in \mathbb {Z}_{p}^{n} \rightarrow \boldsymbol{0} \in \mathbb {Z}_{q}^{m}\), which holds with \(\textsf{negl}\left( \lambda \right) \) probability for a random function. We thus define
and
for \(\boldsymbol{A} ' \in \mathbb {Z}_{p}^{m_p \times (n_p + 1)}\), i.e. extended by one column. Furthermore, we wish to support an additional input \(\boldsymbol{t} \in \mathbb {Z}_{p}^{n}\) to be submitted in the clear. For this, we deploy the standard technique of using a key derivation function to derive a fresh key per tag \(\boldsymbol{t} \) [16, 36]. In particular, let \(\textsf{RO}_{\textsf{key}}: \mathbb {Z}_{p}^{m_p \times n_p} \times \mathbb {Z}_{p}^{n} \rightarrow \mathbb {Z}_{p}^{m_p \times (n_p + 1)}\) be a random oracle, we then define our PRF candidate \(F_{\boldsymbol{A}}^{\textsf{RO}_{\textsf{key}}}(\boldsymbol{t}, \boldsymbol{x})\) in Algorithm 1. Clearly, if \(F_\textsf{pei}(\boldsymbol{A} ', \boldsymbol{y})\) is a PRF then \(F_{\boldsymbol{A}}^{\textsf{RO}_{\textsf{key}}}(\cdot ,\cdot )\) is a PRF with input \((\boldsymbol{t},\boldsymbol{x})\), as \(\boldsymbol{A} _{\boldsymbol{t}}\) in Algorithm 1 is simply a fresh \(F_\textsf{pei}()\) key for each distinct value of \(\boldsymbol{t} \).
3.2 TFHE-Based Instantiation
We ultimately show that the above PRF is highly compatible with TFHE/FHEW, so we describe the OPRF (\(F_\textsf{poprf}\)) using subroutines from the associated literature. The high-level outline of the construction is given as Fig. 3 and a full implementation of TFHE and our OPRF candidate in SageMath is given in [1].
Plaintext Modulus Switching. The main point of interest is in the design of \(F_\textsf{poprf}.\textsf{HEEval}\), which is given in Algorithm 2. The input LWE ciphertexts have plaintext space \(\mathbb {Z}_2\) and the output LWE ciphertexts have plaintext space \(\mathbb {Z}_3\). In order to perform the plaintext modulus switch, we use a variant of TFHE/FHEW bootstrapping that we denote \(\textsf {FHE}.\textsf{CPPBS}_{(p,q)}\). This algorithm is a variation of the standard TFHE programmable bootstrapping algorithm (see [38] for details) augmented with the circuit-private technique of Kluczniak [40]. The difference is that we apply a simple linear transformation and a special “test polynomial”, whilst forgoing the key-switching in [40, Fig. 3].
In more detail, note that general TFHE bootstrapping applies a function \(f : \mathbb {Z}_{2d} \rightarrow \mathbb {Z}_q \) to a plaintext using test polynomial \(v(x) = \sum _{i=0}^{d-1} f(i)\cdot x^i \), assuming the function has negacyclic form i.e. \(f(x) = - f(x+d)\). Recall that TFHE encodes a plaintext \(m \in \mathbb {Z}_p\) as \(m \cdot \lfloor Q/p \rceil \) during encryption and decodes intervals
to \(m \in \mathbb {Z}_p\) during decryption. Consider the simple plaintext switch \(f: \lfloor m \cdot (2d/p) \rceil + e \mapsto m \cdot (Q/q) \) for \(m \in \mathbb {Z}_p\), where \(e\) denotes some LWE error. The corresponding function is not negacyclic, so we would have to restrict plaintext space so that the most significant bit is zero to overcome this. Alternatively, we could apply the techniques of [42] at the cost of two sequential programmable bootstraps. However, in the case \((p,q) = (2,3)\) (which is the one that we use)Footnote 8, one can use the negacyclic function
Although this is a negacyclic function, it maps regions that decrypt to \(m \in \mathbb {Z}_2\) to \(-(m+1) \cdot \lfloor Q/3 \rceil \bmod Q\). To correct this, \(\textsf{CPPBS}_{(2,3)}\) completes by negating the ciphertext and subtracting \(\lfloor Q/3 \rceil \). To summarise, the complete \(\textsf{CPPBS}_{(2,3)}\) procedure takes as input an LWE encryption of \(m \in \mathbb {Z}_2\) and outputs an LWE ciphertext that encrypts \(m\) as an element of \(\mathbb {Z}_3\). We may then optionally apply the ciphertext compression technique from [17] to pack multiple answers into a single RLWE ciphertext (we suppress this step in pseudocode for brevity).
Commitment. A further important alteration is that \(\textsf {FHE}.\textsf{KeyGen}^{(\textsf{pp})}\) will output a commitment to the secret key \(\textsf {FHE}.\textsf{sk}=\boldsymbol{s} \in \mathbb {Z}_2^e\), in addition to the standard public key \(\textsf {FHE}.\textsf{pk}\). In particular, \(\textsf {FHE}.\textsf{KeyGen}^{(\textsf{pp})}()\) begins by running
 and then adds the commitment \(\boldsymbol{b} _{\textsf{pk}}\) to \(\textsf {FHE}.\textsf{pk}\). This commitment takes the form \(\boldsymbol{b} _{\textsf{pk}}=\boldsymbol{A} _{\textsf{pp}}\cdot \boldsymbol{r} + \boldsymbol{e} + \lfloor Q/2 \rfloor \cdot (\boldsymbol{s},\boldsymbol{0}) \in \mathbb {Z}_Q^{N}\), where \(Q\) is the ciphertext modulus, and
and then adds the commitment \(\boldsymbol{b} _{\textsf{pk}}\) to \(\textsf {FHE}.\textsf{pk}\). This commitment takes the form \(\boldsymbol{b} _{\textsf{pk}}=\boldsymbol{A} _{\textsf{pp}}\cdot \boldsymbol{r} + \boldsymbol{e} + \lfloor Q/2 \rfloor \cdot (\boldsymbol{s},\boldsymbol{0}) \in \mathbb {Z}_Q^{N}\), where \(Q\) is the ciphertext modulus, and
 , where \(\chi '\) is a discrete Gaussian of standard deviation \(\beta '\approx 4\) and \(N=2048\) (as in Sect. 2.4). One can view \(\boldsymbol{b} _{\textsf{pk}}\) as a partial symmetric LWE encryption of the secret key from the (T)LWE encryption scheme within TFHE, so \(\chi '\) is simply an error distribution. Therefore, using the same LWE assumption from Sect. 2.4, \(\boldsymbol{b} _{\textsf{pk}}\) is indistinguishable from random and it is easy to check that its presence does not affect the IND-CPA property of TFHE. Furthermore, since \(\boldsymbol{b} _\textsf{pk}\) is simply a randomised function of \((\textsf {FHE}.\textsf{pk}, \textsf {FHE}.\textsf{sk})\), it can be constructed by an adversarial client. Thus, its advantage against semi-honest circuit privacy of \(\textsf {FHE}\) in which the key also contains \(\boldsymbol{b} _{\textsf{pk}}\) remains unchanged. To summarise, the public key material output by \(\textsf {FHE}.\textsf{KeyGen}^{(\textsf{pp})}\) is \(\textsf {FHE}.\textsf{pk}^{(\textsf{pp})} :=(\boldsymbol{b} _{\textsf{pk}},\textsf {FHE}.\textsf{pk})\).
, where \(\chi '\) is a discrete Gaussian of standard deviation \(\beta '\approx 4\) and \(N=2048\) (as in Sect. 2.4). One can view \(\boldsymbol{b} _{\textsf{pk}}\) as a partial symmetric LWE encryption of the secret key from the (T)LWE encryption scheme within TFHE, so \(\chi '\) is simply an error distribution. Therefore, using the same LWE assumption from Sect. 2.4, \(\boldsymbol{b} _{\textsf{pk}}\) is indistinguishable from random and it is easy to check that its presence does not affect the IND-CPA property of TFHE. Furthermore, since \(\boldsymbol{b} _\textsf{pk}\) is simply a randomised function of \((\textsf {FHE}.\textsf{pk}, \textsf {FHE}.\textsf{sk})\), it can be constructed by an adversarial client. Thus, its advantage against semi-honest circuit privacy of \(\textsf {FHE}\) in which the key also contains \(\boldsymbol{b} _{\textsf{pk}}\) remains unchanged. To summarise, the public key material output by \(\textsf {FHE}.\textsf{KeyGen}^{(\textsf{pp})}\) is \(\textsf {FHE}.\textsf{pk}^{(\textsf{pp})} :=(\boldsymbol{b} _{\textsf{pk}},\textsf {FHE}.\textsf{pk})\).
Public Key. Note that although the server does not need to create encryptions itself, we still use the public-key version of TFHE rather than a symmetric-key version as this is useful for circuit privacy [40]. This extra key material in the public key does not impact efficiency noticeably, as the bootstrapping key sizes are the main bottleneck. See the full version for details of \(\textsf{NIZKAoK}_{\textsf{C}}\), and where we fully describe the generation of the bootstrapping keys.
Noise Analysis Overview. Although key-switching may help reduce the number of loops in the blind rotation phase, we will ignore it as we only have bootstrapping depth one, so it is useless in our setting. Additionally, we do not consider key compression here for simplicity (this can be added by amending \(\beta _\textsf{br}\) below). We assume a blind rotation base \(B_{\textsf{br}}\) and set \(\ell _{\textsf{br}} = \lceil \log _{B_{\textsf{br}}}(Q)\rceil \). We also assume the blind rotation key has a noise bound of \(\beta _{\textsf{br}}\). For the final re-randomisation step of circuit-private bootstrapping, we use \(B_{R}\) and \(\lceil \ell _{B_{R}}(Q)\rceil \), assuming a noise bound of \(\beta _{R}\) for the LWE instances. \(\textsf{CPPBS}_{(2,3)}\) leads to exactly the same noise term as a circuit-private bootstrapping, so we just analyse the output of a circuit-private bootstrap (without key-switching).
To describe the correctness requirement, we will use \(\textsf{noise}_{\star }\) to denote an infinity-norm noise bound of ciphertext \(\star \) when viewed as an encryption of the “correct” value. Moving through the computation, we can track error terms as:
-
\(\textsf{noise}_{\textsf{ct}^{(1)}} \le n_p \cdot \textsf{noise}_{\textsf{ct}}\)
-
\(\textsf{noise}_{\textsf{ct}^{(2)}} \le \sqrt{ \sigma ^2_{\textsf{rand}} (1+ \ell _R \sigma _R^2) + \sigma _{\boldsymbol{x}}^2 (1+2nd\sigma ^2_{\textsf{br}}) } \cdot c\) for some appropriately chosen \(c, \sigma _{\textsf{rand}}, \sigma _{\boldsymbol{x}}\) (see Theorem 1)
-
\(\textsf{noise}_{\textsf{ct}^{(3)}} \le m_p \cdot \textsf{noise}_{\textsf{ct}^{(2)}}\).
Let \(e\) denote the TLWE secret key dimension. Then, for correctness, we require that \(\textsf{noise}_{\textsf{ct}^{(1)}} \cdot \frac{2d}{Q} + \frac{e}{2} \le d / 2\) for the \(Q\)-to-\(2d\) mod-switching \(\textsf{ct}\mapsto \lfloor \textsf{ct}\cdot 2d/Q\rceil \) in \(\textsf{CPPBS}_{(2,3)}\), and also that \(\textsf{noise}_{\textsf{ct}^{(3)}} \le Q/3\) for decryption correctness of the unpacked output ciphertext. For circuit privacy, the parameters \(\sigma _\textsf{rand}\) and \(\sigma _{\boldsymbol{x}}\) must be chosen according to Theorem 1. As we see later, for POPRIV1 security, we also need the \(M\text {-}\textsf{LWE}_{\mathbb {Z}_Q,N,\mathbb {Z}_2,\sigma } \), \(M\text {-}\textsf{LWE}_{\mathcal {R} _q,1,\mathbb {Z}_2,\sigma _R} \) and \(M\text {-}\textsf{LWE}_{\mathcal {R} _q,1,\mathbb {Z}_2,\sigma _\textsf{br}} \) assumptions with \(\mathcal {R} _{q} :=\mathbb {Z}_{q}[X]/(X^d+1)\), for the security of the FHE scheme.
Ciphertext Compression. The LWE to RLWE ciphertext packing operation from [17] introduces an additional error whose variance is bounded by \(\frac{d^2-1}{3} \cdot V_{\textsf{ks}}\), where \(V_{\textsf{ks}}\) is the variance of a key-switching operation. In particular, \(V_{\textsf{ks}} = \ell _{\textsf{ks}} \cdot B_{\textsf{ks}}^2 \cdot \sigma _{\textsf{ks}}^2\), where \((\ell _{\textsf {ksk}}, B_{\textsf {ksk}},\sigma _{\textsf {ksk}})\) are analogues to \((\ell _{\textsf{br}}, B_{\textsf{br}},\sigma _{\textsf{br}})\) in a key-switching key context. Therefore, if ciphertext packing is used, the correctness property \(\textsf{noise}_{\textsf{ct}^{(3)}} \le Q/3\) becomes \(\textsf{noise}_{\textsf{ct}^{(3)}} + \sqrt{\frac{d^2-1}{3} \cdot V_{\textsf{ks}}} \cdot c' \le Q/3\), for some appropriately chosen \(c'\). We further assume the hardness of \(M\text {-}\textsf{LWE}_{\mathcal {R} _q,1,\mathbb {Z}_2,\sigma _{\textsf{ks}}} \).
Choosing Parameters and Size Estimates. To pick parameters, we run the script (given in [1]), which checks the noise/correctness constraints and hardness constraints mentioned above. The script additionally includes correctness constraints for the public key compression techniques in [39]. Based on this, we estimate the size of the bootstrapping key (which may be considered an amortisable offline communication cost) as 14.7 MB. The size of the zero-knowledge proofs accompanying this key is 90.7 KB. Applying public-key compression, we instead obtain 2.4 MB and 137.4 KB respectively.
Each request then sends LWE encryptions of \(n_p=256\) bits \(\boldsymbol{m} \) using protected encoded inputs, i.e. \((\boldsymbol{A} ^{(0)}, \boldsymbol{b} :=\boldsymbol{A} ^{(0)} \cdot \boldsymbol{s} + \boldsymbol{e} + \lfloor Q/P \rfloor \cdot \boldsymbol{m})\) where \(\boldsymbol{A} ^{(0)} \in \mathbb {Z}_{Q}^{n_p \times e}\) and \(\boldsymbol{b} \in \mathbb {Z}_{Q}^{n_p}\). Here, \(\boldsymbol{A} ^{(0)}\) can be computed from a small seed of 256 bits. For \(\boldsymbol{b} \) we need to transmit \(n_p \cdot \log Q \) bits. However, as noted in e.g. [43], we may drop the least significant bits. In total we have a ciphertext size of 2.0 KB. The accompanying zero-knowledge proofs take up 63.0 KB but can be amortised to cost about 1.8 KB per query when sending 64 queries in one shot.Footnote 9
The message back from the server is \(m=82\) encryptions of the output elements belonging to \( \mathbb {Z}_{q}\). Here, we cannot expand the dominant uniform matrix \(\boldsymbol{A} ^{(1)}\) from a small seed, but we can drop the least significant bits of \(\boldsymbol{A} ^{(1)}\), since \(\boldsymbol{s} \) is binary. In particular, we may drop, say, the 8 least significant bits and we arrive at \(e \cdot m \cdot 24\) bits for \(\boldsymbol{A} ^{(1)}\). We need \(m \log Q\) bits for \(\boldsymbol{b} \). We can use the same trick of dropping lower order bits for \(\boldsymbol{b} \) again, so we obtain \(82 \cdot 16\) bits. In total we get 480.6 KB. As mentioned above, it is more efficient to pack all return values into a single RLWE sample using techniques from [17], since the cost of transmitting \(\boldsymbol{A} ^{{(1)}}\) dominates here. This does not require additional key material when using public-key compression and reduces the size of response to about 6.2 KB. For more details on these values, see the full version of this paper [1]. The communication performance of our scheme without public key compression has smaller online communication cost, as reported in Table 1.
Remark 3
While our parameter selection is largely conservative in applying worst-case bounds and in adopting the noise sizes required for circuit privacy according to [40, Theorem 1], we deviate from the theorem in setting \(\ell =1\) and \(L < Q\) in (1) when we do not apply public-key compression. This is because the lower-order bits of the decomposed vectors contain only noise. These random bits are then linearly composed with encryptions of \(\boldsymbol{s} \). Thus, the server may simply sample its own random “\(\boldsymbol{s} \)” to perform this computation outputting noise. Not performing this optimisation would increase the size of the public-key by a factor of three. We use \(\ell :=\lceil \log (Q, L) \rceil \) when applying public-key compression.
4 Security
We first prove the pseudorandomness property against malicious clients in Theorem 2 and then privacy (POPRIV1 only) against servers in Theorem 3.
Theorem 2
Let \(\textsf {FHE}\) denote the TFHE scheme with \(q \mid Q\). The construction \(F_\textsf{poprf}\) from Fig. 3 satisfies the POPRF property from Definition 3, with random oracles \(\textsf{RO}_{\textsf{fin}}\) and \(\textsf{RO}_{\textsf{key}}\), if:
-
The client zero-knowledge proof is sound.
-
For any valid \(\textsf{pk}, \textsf{ct}= \textsf {FHE}.\textsf{Enc}({m})\) for \({m} \in \mathbb {Z}_p\), \(\textsf{CPPBS}^{(p,q)}(\textsf{pk}, \textsf{ct})\) is indistinguishable from a fresh LWE ciphertext encrypting \({m}\) as a vector in \(\mathbb {Z}_q\), with some error distribution \(\chi _{\textsf {Sim}}\) as in Theorem 1.
-
The \(\textsf{mat}\text {-}\textsf{NTRU}_{N,P',Q,B}\) assumption holds where \(Q\) is the \(\textsf {FHE}\) modulus.
-
\(P'\) is even and coprime to \(Q\), such that \(Q > B\cdot N\cdot (\beta '+P'\cdot (2\,\beta '+1)/2)\) where \(\beta '\) is the standard deviation used in \(\textsf {FHE}.\textsf{KeyGen}^{(\textsf{pp})}\).
-
\(F_{\cdot }(\cdot , \cdot )\), defined in Sect. 3, is a PRF with output range super-polynomial in the security parameter (e.g. \(2^\lambda \)).
See full version of this paper [1] for the proof.
Remark 4
Note that the security proof asks that \(q \mid Q\). However, parts of the OPRF (e.g. efficient zero-knowledge proofs) might require or benefit from \(Q\) having a specific form that is not a multiple of \(q=3\). This situation can be remedied by applying an LWE modulus switch to a nearby multiple of \(Q\) just after \(\textsf {FHE}.\textsf{CPPBS}\) is applied in Algorithm 2.
Theorem 3
Let \(\textsf {FHE}\) denote the TFHE scheme. The construction \(\mathcal {F}\) from Fig. 3 satisfies the POPRIV1 property if the following hold:
-
\(\textsf {FHE}\) is IND-CPA.
-
The client proof is zero-knowledge.
-
The \(M\text {-}\textsf{LWE}_{\mathbb {Z}_Q,N,\chi ',\chi '} \) assumption holds where \(\chi '=D_{\mathbb {Z},\beta '}\) is the error distribution used in \(\textsf {FHE}.\textsf{KeyGen}^{(\textsf{pp})}\).
The proof is given in the full version of this paper [1].
5 Verifiability
We aim to leverage the oblivious nature of the OPRF to extend our POPRF construction to achieve verifiability. We base our technique on the heuristic trick informally discussed in [2, Sect. 3.2], but with some modifications. In particular, we identify a blind-evaluation attack on this verifiability strategy in our context, the mitigation for which requires sending more “check” material. We then use cryptanalysis to study the security of our protocol, i.e. our construction does not reduce to a known (or even new but clean) hard problem. We view our analysis as an exploration into achieving secure protocols from bounded depth circuits, which we hope has applications beyond this work.
Our verifiability procedure is based on our OPRF presented in Fig. 3 using the cut-and-choose method from [2, Sect. 3.2]. Intuitively, the client, \(\textsf{C}\), sends the server, \(\textsf{S}\), a set of known answer “check” points amongst genuine OPRF queries. The client checks if these check points match the known answer values. It also checks if evaluations on the same points produce the same outputs and if evaluations on different points produce different outputs, here we implicitly rely on the PRP-PRF switching lemma [9]. If these checks pass, we conjecture that the \(\textsf{C}\) may then assume that \(\textsf{S}\) computed the (P)OPRF correctly, assuming appropriate parameters. Let \(\gamma = \nu \cdot \alpha + \beta \) be the number of points \(\textsf{C}\) submits.
-
1.
For some fixed \(\boldsymbol{t} \), \(\textsf{S}\) commits to \(\kappa \) points \(\boldsymbol{z} ^{\star }_{k} :=F_{\boldsymbol{A}}(\boldsymbol{t}, \boldsymbol{x} _k^\star )\) for \(k \in \mathbb {Z}_{\kappa } \) and publishes them (or sends them to \(\textsf{C}\)); \(\textsf{S}\) attaches a \(\textsf{NIZK}\) proof that these are well-formed, i.e. they satisfy the relation
$$\begin{aligned} \mathfrak {R}_{\boldsymbol{t}} :=\left\{ \boldsymbol{t},\, {\{(\boldsymbol{x} ^{\star }_{k}, \boldsymbol{z} ^{\star }_k)\}}_{k \in \mathbb {Z}_{\kappa }};\ \boldsymbol{A} \mid \boldsymbol{z} ^{\star }_k = F_{\boldsymbol{A}}(\boldsymbol{t}, \boldsymbol{x} ^{\star }_{k}) \right\} \end{aligned}$$(2) -
2.
\(\textsf{C}\) wishes to evaluate \(\alpha \) distinct points \(\boldsymbol{x} ^{(\alpha )}_{i}\) for \(i \in \mathbb {Z}_{\alpha }\). It samples
 for \(j \in \mathbb {Z}_{\beta }\). It constructs the vector $$\begin{aligned} \left( \overbrace{\boldsymbol{x} ^{(\alpha )}_{0}, \ldots , \boldsymbol{x} ^{(\alpha )}_{0}}^{\nu \text { copies}}, \ldots , \overbrace{\boldsymbol{x} ^{(\alpha )}_{\alpha -1}, \ldots , \boldsymbol{x} ^{(\alpha )}_{\alpha -1}}^{\nu \text { copies}}, \boldsymbol{x} _{0}^{(\beta )}, \ldots , \boldsymbol{x} ^{(\beta )}_{\beta -1}\right) . \end{aligned}$$
for \(j \in \mathbb {Z}_{\beta }\). It constructs the vector $$\begin{aligned} \left( \overbrace{\boldsymbol{x} ^{(\alpha )}_{0}, \ldots , \boldsymbol{x} ^{(\alpha )}_{0}}^{\nu \text { copies}}, \ldots , \overbrace{\boldsymbol{x} ^{(\alpha )}_{\alpha -1}, \ldots , \boldsymbol{x} ^{(\alpha )}_{\alpha -1}}^{\nu \text { copies}}, \boldsymbol{x} _{0}^{(\beta )}, \ldots , \boldsymbol{x} ^{(\beta )}_{\beta -1}\right) . \end{aligned}$$It then applies a secret permutation \(\rho \), i.e. shuffles the indices, and submits these queries.
-
3.
\(\textsf{C}\) applies \(\rho ^{-1}\) to the responses, i.e. unshuffles the indices, and receives \(\boldsymbol{z} _{i}\). The client \(\textsf{C}\) rejects if any of the following conditions is satisfied:
-
(a)
For \(0 \le k < \alpha \) and for \(i,j \in \mathbb {Z}_{k}\): \(\boldsymbol{z} _{\nu \cdot k + i} \ne \boldsymbol{z} _{\nu \cdot k + j}\), i.e. evaluations on the same point disagree.
-
(b)
For \(0 \le k < \ell < \alpha \) and for \(i,j \in \mathbb {Z}_{k}\): \(\boldsymbol{z} _{\nu \cdot k + i} = \boldsymbol{z} _{\nu \cdot \ell + j}\), i.e. evaluations on different points agree.
-
(c)
For \(0 \le k \le \beta \): \(\boldsymbol{z} _{\nu \cdot \alpha + k} \ne \boldsymbol{z} _{k}^{\star }\), i.e. check points do not match.
Otherwise \(\textsf{C}\) accepts.
-
(a)
We formalise the security definition with a game in Fig. 4. Since the tag \(\boldsymbol{t} \) remains constant throughout we suppress it here. We say a (P)OPRF, \(\mathcal {F}\), is verifiable if the following advantage is negligible in the security parameter \(\lambda \):
Remark 5
We phrase our candidate construction above directly in a batch variant that amortises the overhead of verifiability by submitting \(\alpha \) points together. To recover the usual definition (also used in our security game) of a single evaluation, we may either simply sample \(\alpha -1\) random points and then call our batch variant or submit more check points. This is necessary since \(\gamma \) is a function of \(\alpha \) and \(\beta \) but affects security bounds.
5.1 Verifiability from Levelled HE
Inspired by [18], the heuristic we use to claim security is argues that evaluating a deep circuit in an FHE scheme supporting only shallow circuits is a hard problem. We pursue the same line of reasoning, albeit with significantly tighter security margins. That is, our assumption is significantly stronger than that in [18].
We will assume that the bootstrapping keys for the FHE scheme provided by \(\textsf{C}\) to \(\textsf{S}\) do not provide FHE, but restrict to a limited number of levels. More precisely, we pick parameters such that only Line 3 of Algorithm 2 costs a bootstrapping operation, i.e. all linear operations are realised without bootstrapping. This is already how Algorithm 2 is written, but we foreground this as a security requirement here. We stress that our POPRF in Algorithm 2 can be evaluated in depth one, and that the bootstrapping key submitted to \(\textsf{S}\) presumably prevents it from computing higher depth circuits. This is enabled by the removal of a key-switching key in our (VP)OPRF. See [1] for the construction.
5.2 Cryptanalysis
We explore cheating strategies of a malicious server.
Maximal-Change Guessing. Assume the adversary guesses the positions of the check points in order to make \(\textsf{C}\) accept incorrect outputs, i.e. the adversary behaves honestly on the check points but dishonestly yet consistent on all other points. Recall that \(\gamma = \nu \cdot \alpha + \beta \) is the number of points \(\textsf{C}\) submits to \(\textsf{S}\), where there are \(\beta \) such check point positions. Thus, if we assume semantic security of the underlying HE scheme then the probability of the server guessing correctly is bounded by the probability it selects the positions of a particular check point, for each of the \(\beta \) check points. We obtain a probability \(1/\left( {\begin{array}{c}\gamma \\ \beta \end{array}}\right) \) of guessing correctly.
Minimal-Change Guessing. Assume the adversary’s strategy is to evaluate all points honestly except for one. The consistency check that all \(\nu \) evaluations of the same point must agree and that all other evaluations must disagree, means this adversary has to guess the \(\nu \) positions of the target point. Since there are \(\alpha \) evaluation points, we obtain a probability \(\alpha /\left( {\begin{array}{c}\gamma \\ \nu \end{array}}\right) \) of making a correct guess.
Interpolation. We consider an adversarial \(\textsf{S}\) that uses a circuit \(F_\textsf{pei}'\), of depth at most one, to win the verifiability experiment. At a high level, it solves a quadratic system of equations, assuming one level of bootstrapping allows to implement one multiplication with arity two. More precisely, it chooses \(F_\textsf{pei}'\) such that it agrees on the \(\kappa \) points with of the POPRF circuit \(F_\textsf{pei}(\boldsymbol{A}, \boldsymbol{t}, \cdot )\), but that can differ elsewhere. Since the server knows the check points, this can be trivially done. To prevent such an attack, one would need to publish \(\kappa =n + \frac{n}{2}(n+1)+\mathcal {O}(1)\) check points where \(n\) is the input/output dimension. This, implies no quadratic polynomial interpolation exists. If we let \(\kappa =128^2\), then the communication cost of check points is approximately an additional 0.5 MB, which can be reduced to 256 KB by generating the input values from a seed.
Check and Cheat. Finally, we consider that the adversary is able to construct a shallow cheating circuit, which is described in Algorithm 3, with \([\cdot ]\) denoting a homomorphic encryption of a value. Intuitively, it homomorphically checks the clients inputs against known answers, and then homomorphically selects which output to return. This circuit has depth two.
Parameters. We may aim for 80-bit security against the statistical guessing attacks above while assuming \(\kappa =128\) and a depth-one check and cheat algorithm does not exist. To do so, we set \(\gamma =1165\), \(\beta =10, \nu =11\) and thus \(\alpha =105\). This implies a multiplicative size overhead of \(\approx 11.1\) to heuristically upgrade the OPRF to a VOPRF.
5.3 Security Reduction
Finally, we establish that our verifiability property implies POPRIV2 under some additional assumptions.
Theorem 4
Our VPOPRF construction satisfies POPRIV2 if
-
\(F_\textsf{vpoprf}\) satisfies POPRIV1.
-
\(F_\textsf{vpoprf}\) is verifiable.
-
\(\text {NIZKAoK}_{\mathfrak {R}_{\boldsymbol{t}}}\) is sound for \(\mathfrak {R}_{\boldsymbol{t}}\) defined in (2).
The proof is given in the full version of this paper [1].
6 Proof-of-Concept Implementations
SageMath. In the full version of this paper [1], we give a SageMath [50] implementation of TFHE and our OPRF candidate. This implementation is meant to establish and clarify ideas and thus we do not provide benchmarks for it. Our implementation is complete with respect to the core functionality. In particular, we provide a new from-scratch implementation of TFHE [21] in tfhe.py, of circuit-private TFHE bootstrapping [40] in cpbs.py, and ciphertext and bootstrapping-key compression [17, 39] in compression.py. Our OPRF in oprf.py is then relatively simple and calls the appropriate library functions. We re-implemented the underlying machinery since we are not aware of public implementations that provide all these features yet. We did not implement the zero-knowledge proof systems from [44] and [10] since those are somewhat orthogonal to the focus of this work. We did, however, as indicated earlier, adapt or re-implement scripts for estimating their (combined) proof sizes.
Rust Benchmarks. To give a sense of performance, we also implemented the key operations relied upon by our OPRF in Rust. In particular, we use Zama’s tfhe-rs FHE library [21]. Unfortunately, several functionalities we rely on are not (yet) implemented in tfhe-rs: circuit privacy, ciphertext and public-key compression. Moreover, tfhe-rs assumes throughout that plaintext moduli are powers of two, which is incompatible with our OPRF. The most costly operations are the client’s \(F_\textsf{poprf}.\textsf{KeyGen}\) and the server’s \(F_\textsf{poprf}.\textsf{BlindEal}\), which we discuss next.Footnote 10
In our benchmarks \(F_\textsf{poprf}.\textsf{KeyGen}\) took \(1\) s. While this contains neither proving well-formedness nor compressing the public-key, we expect neither to be significantly more expensive. Even so, this operation can be regarded as a one-time cost in many applications. For example, considering OPAQUE [37], clients and servers already register persistent identifiers for each other (such as the client-specific OPRF key). Therefore, the client keypair can be registered as part of this process. Similarly for Privacy Pass [22], the issuance phase of the protocol does not discount clients from registering persistent information that they use whenever they make VOPRF evaluations (which could include this key information). As a result, in many applications, clients will generate a single FHE keypair and use that over multiple interactions with the server.
For the online server-side algorithm (\(F_\textsf{poprf}.\textsf{BlindEal}\)), the runtime in our benchmarks was \(151\) ms, which may be quick enough for certain applications that have a hard requirement to ensure post-quantum security. However, as mentioned above, this costs “plain” and not circuit-private boostrapping which would be significantly more expensive.Footnote 11 On the other hand, as mentioned under open problems, it is plausible that cheaper alternatives to full circuit privacy might suffice for our setting. More broadly, we note that hardware acceleration of this step is a viable option, cf. [8]. In any case, previous classical constructions of (P)OPRFs, such as [51] take only a few ms to run the server evaluation, so the efficiency gap between our FHE-based approach and previous work is evident.
These results were acquired by using a server with 96 Intel Xeon Gold 6252 CPU @ 2.10 GHz cores and 768 GB of RAM. Server evaluation was run with parallelisation enabled, meaning that each multiplication of the client input encrypted vector with a matrix column is run in its own separate thread, but we only use 64 threads/cores.Footnote 12 Client evaluations use only a single core. Each of the benchmarks was established after running it ten times and taking the average runtime. Our benchmarking code is available at https://github.com/alxdavids/oprf-fhe-ec24-artifact.
Notes
- 1.
The security of the PRF candidate in [11] rests on the absence of any low-degree polynomial interpolating it, ruling out efficient implementations using FHE schemes that only provide additions and multiplications.
- 2.
These are: plaintext moduli that are not powers of two, circuit privacy, ciphertext and bootstrapping-key compression.
- 3.
We note that while the large sizes for achieving malicious security in [2] can be avoided using improved NIZKs, the semi-honest base size of 2 MB per query stems from requiring \(q\approx 2^{256}\) for statistical correctness and security arguments.
- 4.
We note that quantum algorithms offer only marginal, i.e. less than square-root, speedups here [3].
- 5.
This allows to restrict the number of sequential bootstrappings that can be performed.
- 6.
As it stands, this strong PRF candidate maps zero to zero and is thus trivially distinguished from a random function, we will address this below.
- 7.
If the reader’s PDF viewer does not support PDF attachments (e.g. Preview on MacOS does not), then e.g. pdfdetach can be used to extract these files.
- 8.
Note that we may pick \(q \ne 3\) but require \(p=2\).
- 9.
All of these figures assume that we apply public-key compression.
- 10.
\(F_\textsf{poprf}.\textsf{Request}\) runs in \(28.9\) ms and \(F_\textsf{poprf}.\textsf{Finalise}\) in \(0.2\) ms in our benchmarks. The former does not include the time to prove well-formedness, but – as below – we do not expect this to radically change this picture.
- 11.
Table 3 of [40] reports an overhead of 5x to 10x for circuit privacy.
- 12.
On a single core, server blind evaluation took \(7.1\) s.
References
Albrecht, M.R., Davidson, A., Deo, A., Gardham, D.: Crypto dark matter on the Torus: oblivious PRFs from shallow PRFs and FHE. Cryptology ePrint Archive, Report 2023/232 (2023). https://eprint.iacr.org/2023/232
Albrecht, M.R., Davidson, A., Deo, A., Smart, N.P.: Round-optimal verifiable oblivious pseudorandom functions from ideal lattices. In: Garay [30], pp. 261–289 (2019). https://eprint.iacr.org/2019/1271
Albrecht, M.R., Gheorghiu, V., Postlethwaite, E.W., Schanck, J.M.: Estimating quantum speedups for lattice sieves. In: Moriai and Wang [47], pp. 583–613 (2020)
Albrecht, M.R., Player, R., Scott, S.: On the concrete hardness of learning with errors. J. Math. Cryptol. 9(3), 169–203 (2015)
Albrecht, M.R., Rechberger, C., Schneider, T., Tiessen, T., Zohner, M.: Ciphers for MPC and FHE. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part I. LNCS, vol. 9056, pp. 430–454. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_17
Basso, A.: A post-quantum round-optimal oblivious PRF from isogenies. Cryptology ePrint Archive, Report 2023/225 (2023). https://eprint.iacr.org/2023/225
Basso, A., Kutas, P., Merz, S.-P., Petit, C., Sanso, A.: Cryptanalysis of an oblivious PRF from supersingular isogenies. In: Tibouchi, M., Wang, H. (eds.) ASIACRYPT 2021, Part I. LNCS, vol. 13090, pp. 160–184. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-92062-3_6
Van Beirendonck, M., D’Anvers, J.-P., Verbauwhede, I.: FPT: a fixed-point accelerator for torus fully homomorphic encryption. Cryptology ePrint Archive, Report 2022/1635 (2022). https://eprint.iacr.org/2022/1635
Bellare, M., Rogaway, P.: The security of triple encryption and a framework for code-based game-playing proofs. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 409–426. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_25
Beullens, W., Seiler, G.: LaBRADOR: compact proofs for R1CS from module-SIS. Cryptology ePrint Archive, Report 2022/1341 (2022). https://eprint.iacr.org/2022/1341
Boneh, D., Ishai, Y., Passelègue, A., Sahai, A., Wu, D.J.: Exploring crypto dark matter: new simple PRF candidates and their applications. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018, Part II, vol. 11240. LNCS, pp. 699–729. Springer, Heidelberg (2018). Full version available at https://eprint.iacr.org/2018/1218
Boneh, D., Kogan, D., Woo, K.: Oblivious pseudorandom functions from isogenies. In: Moriai and Wang [47], pp. 520–550 (2020)
Bourse, F., del Pino, R., Minelli, M., Wee, H.: FHE circuit privacy almost for free. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. Part II, volume 9815 of LNCS, pp. 62–89. Springer, Heidelberg (2016)
Boyle, E., et al.: Correlated pseudorandomness from expand-accumulate codes. In: Dodis and Shrimpton [24], pp. 603–633 (2022)
Brakerski, Z., Gentry, C., Vaikuntanathan, V.: Fully homomorphic encryption without bootstrapping. Cryptology ePrint Archive, Report 2011/277 (2011). https://eprint.iacr.org/2011/277
Casacuberta, S., Hesse, J., Lehmann, A.: SoK: oblivious pseudorandom functions. In: 7th IEEE European Symposium on Security and Privacy, EuroS &P 2022, pp. 625–646. IEEE (2022)
Chen, H., Dai, W., Kim, M., Song, Y.: Efficient homomorphic conversion between (Ring) LWE ciphertexts. In: Sako, K., Tippenhauer, N.O. (eds.) ACNS 2021, Part I. LNCS, vol. 12726, pp. 460–479. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-78372-3_18
Chen, H., Huang, Z., Laine, K., Rindal, P.: Labeled PSI from fully homomorphic encryption with malicious security. In: Lie, D., Mannan, M., Backes, M., Wang, X. (eds.) ACM CCS 2018, pp. 1223–1237. ACM Press, October 2018
Cheon, J.H., Cho, W., Kim, J.H., Kim, J.: Adventures in crypto dark matter: attacks and fixes for weak pseudorandom functions. In: Garay [30], pp. 739–760 (2020)
Cheon, J.H., Kim, A., Kim, M., Song, Y.: Homomorphic encryption for arithmetic of approximate numbers. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part I. LNCS, vol. 10624, pp. 409–437. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_15
Chillotti, I., Gama, N., Georgieva, M., Izabachène, M.: TFHE: fast fully homomorphic encryption over the torus. J. Cryptol. 33(1), 34–91 (2020)
Davidson, A., Goldberg, I., Sullivan, N., Tankersley, G., Valsorda, F.: Privacy pass: bypassing internet challenges anonymously. PoPETs 2018(3), 164–180 (2018)
Dinur, I., et al.: MPC-friendly symmetric cryptography from alternating moduli: candidates, protocols, and applications. In: Malkin, T., Peikert, C. (eds.) CRYPTO 2021, Part IV. LNCS, vol. 12828, pp. 517–547. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-84259-8_18
Dodis, Y., Shrimpton, T. (eds.): CRYPTO 2022, Part II. LNCS, vol. 13508. Springer, Heidelberg (2022)
Ducas, L., Stehlé, D.: Sanitization of FHE ciphertexts. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part I. LNCS, vol. 9665, pp. 294–310. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_12
Ducas, L., van Woerden, W.: NTRU fatigue: how stretched is overstretched? In: Tibouchi, M., Wang, H. (eds.) ASIACRYPT 2021, Part IV. LNCS, vol. 13093, pp. 3–32. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-92068-5_1
Everspaugh, A., Chatterjee, R., Scott, S., Juels, A., Ristenpart, T.: The Pythia PRF service. In: Jung, J., Holz, T. (eds.) USENIX Security 2015, pp. 547–562. USENIX Association, August 2015
Faller, S., Ottenhues, A., Ernst, J.: Composable oblivious pseudo-random functions via garbled circuits. Cryptology ePrint Archive, Paper 2023/1176 (2023). https://eprint.iacr.org/2023/1176
Fan, J., Vercauteren, F.: Somewhat practical fully homomorphic encryption. Cryptology ePrint Archive, Report 2012/144 (2012). https://eprint.iacr.org/2012/144
Garay, J. (ed.): PKC 2021, Part II. LNCS, vol. 12711. Springer, Heidelberg (2021)
Gentry, C.: A fully homomorphic encryption scheme. Ph.D. thesis, Stanford University (2009). crypto.stanford.edu/craig
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_5
Goldreich, O.: Foundations of Cryptography, vol. 2. Cambridge University Press, Cambridge (2004)
Heimberger, L., Meisingseth, F., Rechberger, C.: OPRFs from isogenies: designs and analysis. Cryptology ePrint Archive, Paper 2023/639 (2023). https://eprint.iacr.org/2023/639
Hoffstein, J., Pipher, J., Silverman, J.H.: NTRU: a new high speed public key cryptosystem. Draft Distributed at Crypto (1996). http://web.securityinnovation.com/hubfs/files/ntru-orig.pdf
Jarecki, S., Krawczyk, H., Resch, J.: Threshold partially-oblivious PRFs with applications to key management. Cryptology ePrint Archive, Report 2018/733 (2018). https://eprint.iacr.org/2018/733
Jarecki, S., Krawczyk, H., Xu, J.: OPAQUE: an asymmetric PAKE protocol secure against pre-computation attacks. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part III. LNCS, vol. 10822, pp. 456–486. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_15
Joye, M.: Guide to fully homomorphic encryption over the [discretized] torus. Cryptology ePrint Archive, Report 2021/1402 (2021). https://eprint.iacr.org/2021/1402
Kim, A., Lee, Y., Deryabin, M., Eom, J., Choi, R.: LFHE: fully homomorphic encryption with bootstrapping key size less than a megabyte. Cryptology ePrint Archive, Paper 2023/767 (2023). https://eprint.iacr.org/2023/767
Kluczniak, K.: Circuit privacy for FHEW/TFHE-style fully homomorphic encryption in practice. Cryptology ePrint Archive, Report 2022/1459 (2022). https://eprint.iacr.org/2022/1459
Langlois, A., Stehlé, D.: Worst-case to average-case reductions for module lattices. DCC 75(3), 565–599 (2015)
Liu, Z., Micciancio, D., Polyakov, Y.: Large-precision homomorphic sign evaluation using FHEW/TFHE bootstrapping. In: Agrawal, S., Lin, D. (eds.) ASIACRYPT 2022. Part II, vol. 13792. LNCS, pp. 130–160. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-22966-4_5
Lyubashevsky, V., et al.: CRYSTALS-Dilithium. Technical report, National Institute of Standards and Technology (2022). https://csrc.nist.gov/Projects/post-quantum-cryptography/selected-algorithms-2022
Lyubashevsky, V., Nguyen, N.K., Plançon, M.: Lattice-based zero-knowledge proofs and applications: shorter, simpler, and more general. In: Dodis and Shrimpton [24], pp. 71–101 (2022)
MATZOV. Report on the Security of LWE: Improved Dual Lattice Attack, April 2022. https://doi.org/10.5281/zenodo.6412487
Micciancio, D., Polyakov, Y.: Bootstrapping in FHEW-like cryptosystems. Cryptology ePrint Archive, Report 2020/086 (2020). https://eprint.iacr.org/2020/086
Moriai, S., Wang, H. (eds.): ASIACRYPT 2020, Part II. LNCS, vol. 12492. Springer, Heidelberg (2020)
Seres, I.A., Horváth, M., Burcsi, P.: The Legendre pseudorandom function as a multivariate quadratic cryptosystem: security and applications. Cryptology ePrint Archive, Report 2021/182 (2021). https://eprint.iacr.org/2021/182
Shoup, V., Gennaro, R.: Securing threshold cryptosystems against chosen ciphertext attack. In: Nyberg, K. (ed.) EUROCRYPT 1998. LNCS, vol. 1403, pp. 1–16. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054113
Stein, W., et al.: Sage Mathematics Software Version 9.8. The Sage Development Team (2023). http://www.sagemath.org
Tyagi, N., Celi, S., Ristenpart, T., Sullivan, N., Tessaro, S., Wood, C.A.: A fast and simple partially oblivious PRF, with applications. In: Dunkelman, O., Dziembowski, S. (eds.) EUROCRYPT 2022, Part II, vol. 13276. LNCS, pp. 674–705. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-07085-3_23
Unruh, D.: Quantum proofs of knowledge. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 135–152. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_10
Acknowledgements
We thank Christian Weinert for discussing MPC approaches with us; Ilaria Chillotti, Ben Curtis and Jean-Baptiste Orfila for answering questions about TFHE and tfhe-rs; Nicolas Gama for answering questions about TFHE. We thank Ward Beullens and Gregor Seiler for answering questions about LaBRADOR and sharing their size estimation Pari/GP script.
The research of Martin Albrecht was supported by UKRI grants EP/S02-0330/1, EP/-S02087X/1, EP/Y02432X/1 and by the European Union Horizon 2020 Research and Innovation Program Grant 780701. The research of Alex Davidson was supported by NOVA LINCS (UIDB/04516/2020), with the financial support of FCT.IP. Part of this work was done while Martin Albrecht was at Royal Holloway, University of London, while Alex Davidson was at Brave Software, and while Amit Deo was at Crypto Quantique.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
1 Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Copyright information
© 2024 International Association for Cryptologic Research
About this paper
Cite this paper
Albrecht, M.R., Davidson, A., Deo, A., Gardham, D. (2024). Crypto Dark Matter on the Torus. In: Joye, M., Leander, G. (eds) Advances in Cryptology – EUROCRYPT 2024. EUROCRYPT 2024. Lecture Notes in Computer Science, vol 14656. Springer, Cham. https://doi.org/10.1007/978-3-031-58751-1_16
Download citation
DOI: https://doi.org/10.1007/978-3-031-58751-1_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-58750-4
Online ISBN: 978-3-031-58751-1
eBook Packages: Computer ScienceComputer Science (R0)




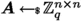
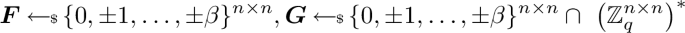
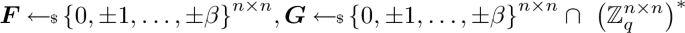



 for
for 

