Abstract
A sequential aggregate signature (SAS) scheme allows multiple users to sequentially combine their respective signatures in order to reduce communication costs. Historically, early proposals required the use of trapdoor permutation (e.g., RSA). In recent years, a number of attempts have been made to extend SAS schemes to post-quantum assumptions. Many post-quantum signatures have been proposed in the hash-and-sign paradigm, which requires the use of trapdoor functions and appears to be an ideal candidate for sequential aggregation attempts. However, the hardness in achieving post-quantum one-way permutations makes it difficult to obtain similarly general constructions. Direct attempts at generalizing permutation-based schemes have been proposed, but they either lack formal security or require additional properties on the trapdoor function, which are typically not available for multivariate or code-based functions. In this paper, we propose a (partial-signature) history-free SAS within the probabilistic hash-and-sign with retry paradigm, generalizing existing techniques to generic trapdoor functions. We prove the security of our scheme in the random oracle model and we instantiate our construction with three post-quantum schemes, comparing their compression capabilities. Finally, we discuss how direct extensions of permutation-based SAS schemes are not possible without additional properties, showing the lack of security of two existing multivariate schemes.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
- 2.
In this case we would have that \(\alpha (\boldsymbol{{x}}) = \textbf{A}\boldsymbol{{x}}\) with \(\textbf{A} = [\textbf{I}_m \mathbin \vert \textbf{0}_{m,n-m}]\).
- 3.
For instance, this is the case for Trapdoor Preimage Sampleable Function [24].
- 4.
This happens with probability approximately \(1-1/q\).
References
Ahn, J.H., Green, M., Hohenberger, S.: Synchronized aggregate signatures: new definitions, constructions and applications. In: Al-Shaer, E., Keromytis, A.D., Shmatikov, V. (eds.) ACM CCS 2010, pp. 473–484. ACM Press (2010). https://doi.org/10.1145/1866307.1866360
Albrecht, M.R., Cini, V., Lai, R.W.F., Malavolta, G., Thyagarajan, S.A.K.: Lattice-based SNARKs: publicly verifiable, preprocessing, and recursively composable - (extended abstract). In: Dodis, Y., Shrimpton, T. (eds.) CRYPTO 2022, Part II. LNCS, vol. 13508, pp. 102–132. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-15979-4_4
Banegas, G., Debris-Alazard, T., Nedeljković, M., Smith, B.: Wavelet: code-based postquantum signatures with fast verification on microcontrollers. Cryptology ePrint Archive, Report 2021/1432 (2021). https://eprint.iacr.org/2021/1432
Bellare, M., Namprempre, C., Neven, G.: Unrestricted aggregate signatures. In: Arge, L., Cachin, C., Jurdziński, T., Tarlecki, A. (eds.) ICALP 2007. LNCS, vol. 4596, pp. 411–422. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73420-8_37
Bellare, M., Neven, G.: Multi-signatures in the plain public-key model and a general forking lemma. In: Juels, A., Wright, R.N., De Capitani di Vimercati, S. (eds.) ACM CCS 2006, pp. 390–399. ACM Press (2006). https://doi.org/10.1145/1180405.1180453
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: Denning, D.E., Pyle, R., Ganesan, R., Sandhu, R.S., Ashby, V. (eds.) ACM CCS 1993, pp. 62–73. ACM Press (1993). https://doi.org/10.1145/168588.168596
Beullens, W.: Improved cryptanalysis of UOV and rainbow. In: Canteaut, A., Standaert, F.-X. (eds.) EUROCRYPT 2021, Part I. LNCS, vol. 12696, pp. 348–373. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-77870-5_13
Beullens, W.: MAYO: practical post-quantum signatures from oil-and-vinegar maps. In: AlTawy, R., Hülsing, A. (eds.) SAC 2021. LNCS, vol. 13203, pp. 355–376. Springer, Cham (2022). https://doi.org/10.1007/978-3-030-99277-4_17
Beullens, W., Campos, F., Celi, S., Hess, B., Kannwischer, M.J.: MAYO. Technical report, National Institute of Standards and Technology (2023). https://csrc.nist.gov/Projects/pqc-dig-sig/round-1-additional-signatures
Beullens, W., et al.: UOV—Unbalanced Oil and Vinegar. Technical report, National Institute of Standards and Technology (2023). https://csrc.nist.gov/Projects/pqc-dig-sig/round-1-additional-signatures
Boneh, D., Gentry, C., Lynn, B., Shacham, H.: Aggregate and verifiably encrypted signatures from bilinear maps. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 416–432. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_26
Boudgoust, K., Takahashi, A.: Sequential half-aggregation of lattice-based signatures. Cryptology ePrint Archive, Report 2023/159 (2023). https://eprint.iacr.org/2023/159
Brogle, K., Goldberg, S., Reyzin, L.: Sequential aggregate signatures with lazy verification from trapdoor permutations. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 644–662. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_39
Chailloux, A., Debris-Alazard, T.: Tight and optimal reductions for signatures based on average trapdoor preimage sampleable functions and applications to code-based signatures. In: Kiayias, A., Kohlweiss, M., Wallden, P., Zikas, V. (eds.) PKC 2020, Part II. LNCS, vol. 12111, pp. 453–479. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45388-6_16
Chen, J., Ling, J., Ning, J., Peng, Z., Tan, Y.: MQ aggregate signature schemes with exact security based on UOV signature. In: Liu, Z., Yung, M. (eds.) Inscrypt 2019. LNCS, vol. 12020, pp. 443–451. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-42921-8_26
Chen, Y., Zhao, Y.: Half-aggregation of Schnorr signatures with tight reductions. In: Atluri, V., Di Pietro, R., Jensen, C.D., Meng, W. (eds.) ESORICS 2022, Part II. LNCS, vol. 13555, pp. 385–404. Springer, Heidelberg (2022). https://doi.org/10.1007/978-3-031-17146-8_19
Debris-Alazard, T., Sendrier, N., Tillich, J.-P.: Wave: a new family of trapdoor one-way preimage sampleable functions based on codes. In: Galbraith, S.D., Moriai, S. (eds.) ASIACRYPT 2019, Part I. LNCS, vol. 11921, pp. 21–51. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-34578-5_2
Devadas, L., Goyal, R., Kalai, Y., Vaikuntanathan, V.: Rate-1 non-interactive arguments for batch-NP and applications. In: 63rd FOCS, pp. 1057–1068. IEEE Computer Society Press (2022). https://doi.org/10.1109/FOCS54457.2022.00103
El Bansarkhani, R., Buchmann, J.: Towards lattice based aggregate signatures. In: Pointcheval, D., Vergnaud, D. (eds.) AFRICACRYPT 2014. LNCS, vol. 8469, pp. 336–355. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-06734-6_21
El Bansarkhani, R., Mohamed, M.S.E., Petzoldt, A.: MQSAS - a multivariate sequential aggregate signature scheme. In: Bishop, M., Nascimento, A.C.A. (eds.) ISC 2016. LNCS, vol. 9866, pp. 426–439. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45871-7_25
Fischlin, M., Lehmann, A., Schröder, D.: History-free sequential aggregate signatures. In: Visconti, I., De Prisco, R. (eds.) SCN 2012. LNCS, vol. 7485, pp. 113–130. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32928-9_7
Fleischhacker, N., Simkin, M., Zhang, Z.: Squirrel: efficient synchronized multi-signatures from lattices. In: Yin, H., Stavrou, A., Cremers, C., Shi, E. (eds.) ACM CCS 2022, pp. 1109–1123. ACM Press (2022). https://doi.org/10.1145/3548606.3560655
Gentry, C., O’Neill, A., Reyzin, L.: A unified framework for trapdoor-permutation-based sequential aggregate signatures. In: Abdalla, M., Dahab, R. (eds.) PKC 2018, Part II. LNCS, vol. 10770, pp. 34–57. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76581-5_2
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Ladner, R.E., Dwork, C. (eds.) 40th ACM STOC, pp. 197–206. ACM Press (2008). https://doi.org/10.1145/1374376.1374407
Gentry, C., Ramzan, Z.: Identity-based aggregate signatures. In: Yung, M., Dodis, Y., Kiayias, A., Malkin, T. (eds.) PKC 2006. LNCS, vol. 3958, pp. 257–273. Springer, Heidelberg (2006). https://doi.org/10.1007/11745853_17
Goubin, L., et al.: PROV—PRovable unbalanced Oil and Vinegar. Technical report, National Institute of Standards and Technology (2023). https://csrc.nist.gov/Projects/pqc-dig-sig/round-1-additional-signatures
Kipnis, A., Patarin, J., Goubin, L.: Unbalanced oil and vinegar signature schemes. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 206–222. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_15
Kosuge, H., Xagawa, K.: Probabilistic hash-and-sign with retry in the quantum random oracle model. Cryptology ePrint Archive, Report 2022/1359 (2022). https://eprint.iacr.org/2022/1359
Levitskaya, A.: Systems of random equations over finite algebraic structures. Cybern. Syst. Anal. 41, 67–93 (2005)
Lu, S., Ostrovsky, R., Sahai, A., Shacham, H., Waters, B.: Sequential aggregate signatures and multisignatures without random oracles. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 465–485. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_28
Lysyanskaya, A., Micali, S., Reyzin, L., Shacham, H.: Sequential aggregate signatures from trapdoor permutations. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 74–90. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_5
Neven, G.: Efficient sequential aggregate signed data. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 52–69. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_4
Prest, T., et al.: FALCON. Technical report, National Institute of Standards and Technology (2022). https://csrc.nist.gov/Projects/post-quantum-cryptography/selected-algorithms-2022
Sakumoto, K., Shirai, T., Hiwatari, H.: On provable security of UOV and HFE signature schemes against chosen-message attack. In: Yang, B.-Y. (ed.) PQCrypto 2011. LNCS, vol. 7071, pp. 68–82. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25405-5_5
Wang, Z., Wu, Q.: A practical lattice-based sequential aggregate signature. In: Steinfeld, R., Yuen, T.H. (eds.) ProvSec 2019. LNCS, vol. 11821, pp. 94–109. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-31919-9_6
Acknowledgments
The authors would like to thank the anonymous reviewers of CT-RSA 2024 for their valuable feedback and suggestions. This publication was created with the co-financing of the European Union FSE-REACT-EU, PON Research and Innovation 2014–2020 DM1062/2021. The first author is a member of the INdAM Research Group GNSAGA. The second author is a member of CrypTO, the group of Cryptography and Number Theory of Politecnico di Torino. The first author acknowledges support from Ripple’s University Blockchain Research Initiative.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Missing Proofs
Lemma 2
When a new node is added to the \(\textsf{HTree}\) as a result to a call to \(\textsf{H}\), the additional value \(y'\) is chosen uniformly at random from \(\mathcal {Y}\).
Proof
When a new node is added to the \(\textsf{HTree}\) on Line 23 of \(\textsf{H}\), there are two possibilities for the additional value \(y'\). In both cases, \(y'\) is chosen uniformly at random from \(\mathcal {Y}\) and is independent of the view of \(\mathcal {A}\). In fact, whenever the query to \(\textsf{H}\) is not the special random guess \(c^{\star }\) chosen by the simulator, we have \(y' \leftarrow \textsf{G}(h') \oplus \alpha \). Here, \(\textsf{G}(h')\) is guaranteed to be a fresh uniformly random value since, otherwise, \(\textsf{H}\) would abort on Line 16 and the node would not be added to the \(\textsf{HTree}\). If, on the other hand, the query \(c^{\star }\) was made to \(\textsf{H}\), then we set \(y' \leftarrow y^{\star }\) for one of the new nodes to be added. Since \(c^{\star }\) was chosen randomly among all queries to \(\textsf{H}\), the assignment of \(y^{\star }\) is made independently of the view of \(\mathcal {A}\) and previous interactions with \(\textsf{H}\). \(\square \)
Lemma 3
For any \(k > \psi \) functions \(\textsf{F}_1, \ldots , \textsf{F}_k :\mathcal {X}\rightarrow \mathcal {Y}\) and uniformly random \(y_1, \ldots , y_k \in \mathcal {Y}\), there exists \(x \in \mathcal {X}\) such that \(\textsf{F}_i(x) = y_i\), for every \(i = 1, \ldots , k\), with probability at most \(|\mathcal {X}|/|\mathcal {Y}|^{k}\).
Proof
Let \(S^{\textsf{F}}_y = \{x \in \mathcal {X}: \textsf{F}(x) = y \}\) be the set of preimages of y under \(\textsf{F}\). For a random choice of \(y_1\) it holds that \(|S^{\textsf{F}_{1}}_{y_1} |= \alpha \) for some \(0 \le \alpha \le |\mathcal {X}|\). Then, there are at most \(\alpha \) possible values for the tuple \((y_2, \ldots , y_k)\), corresponding to \(\left\{ (\textsf{F}_2(x), \ldots , \textsf{F}_k(x)): x \in S^{\textsf{F}_{1}}_{y_1}\right\} \), such that \(\bigcap S^{\textsf{F}_{i}}_{y_i} \ne \emptyset \). Since \(y_2, \ldots , y_k\) are uniformly chosen in \(\mathcal {Y}\), the probability of a non-empty intersection is at most \(\alpha |\mathcal {Y}|^{1-k}\). Therefore, the desired probability is bounded by varying over the possible values of \(\alpha \):

\(\square \)
Lemma 4
If an input Q has not been entered in the \(\textsf{HTree}\) after being queried to \(\textsf{H}\), the probability that it will ever become tethered to a node in \(\textsf{HTree}\) is at most \(\psi \textsf{q}'/|\mathcal {Y}|\), where \(\textsf{q}'\) is the number of queries made to \(\textsf{H}\) after Q.
Proof
Suppose that \(Q = (\textsf{F}, m, r, x)\) was queried to \(\textsf{H}\) and was not added to the \(\textsf{HTree}\), i.e. \(\textsf{Lookup}(x) = \bot \). Now suppose that a query \(Q' = (\textsf{F}', m', r', x')\) was subsequently sent to \(\textsf{H}\) and was added to \(\textsf{HTree}\) as part of a node \(N'\) with additional value \(y'\). For Q to be tethered to \(N'\), it must hold that \(\textsf{F}'(x) = y'\). Following Lemma 2, when a new node is added to the \(\textsf{HTree}\) as a result to a call to \(\textsf{H}\), the additional value \(y'\) is chosen uniformly at random from \(\mathcal {Y}\). In particular, \(y'\) is random and independent of \(\textsf{F}'\) and x. Therefore, the probability of having \(\textsf{F}'(x) = y'\) is \(|\mathcal {Y}|^{-1}\). Since there are at most \(\textsf{q}'\) queries to \(\textsf{H}\) after Q and each query can add at most \(\psi \) nodes to the \(\textsf{HTree}\), the desired probability follows by the union bound. \(\square \)
1.1 A.1 Proof for strong \(\mathrm {PS\hbox {-}HF\hbox {-}UF\hbox {-}CMA}\) security (Theorem 1)
Proof
We prove the reduction by presenting a sequence of hybrid games, modifying the strong \(\mathrm {PS\hbox {-}HF\hbox {-}UF\hbox {-}CMA}\) game (Game 2) until it can be simulated by the \(\textrm{OW}\) adversary \(\mathcal {B}\). In the following use the notation \({\text {Pr}}\!\!\left[ \textsf{Game}_{\textsf{n}}(\mathcal {A}) = 1\right] \) to denote the probability that \(\textsf{Game}_{\textsf{n}}\) returns 1 when playing by \(\mathcal {A}\). The game sequence \(\textsf{Game}_\textsf{0}\)-\(\textsf{Game}_\textsf{3}\) for \(\textsf{O}{\textsf{AggSign}}\) is detailed in Game 4. The game sequence \(\textsf{Game}_\textsf{3}\)-\(\textsf{Game}_\textsf{5}\) for \(\textsf{H}\) is detailed in Game 5.

-
\({\textsf{Game}_\textsf{0}}\) This is the original strong \(\mathrm {PS\hbox {-}HF\hbox {-}UF\hbox {-}CMA}\) game against the \(\mathsf {HaS\hbox {-}HF\hbox {-}SAS}\) scheme except that it uses programmable random oracles. At the start of the game, the challenger initializes two tables, \(\textsf{HT}\) for \(\textsf{H}\) and \(\textsf{GT}\) for \(\textsf{G}\). When a query Q for \(\textsf{H}\) is received, if \(\textsf{HT}[Q] = \bot \) it uniformly samples
 and stores \(\textsf{HT}[Q] \leftarrow \eta \), finally it returns \(\textsf{HT}[Q]\) (similarly for \(\textsf{G}\)). It follows that
and stores \(\textsf{HT}[Q] \leftarrow \eta \), finally it returns \(\textsf{HT}[Q]\) (similarly for \(\textsf{G}\)). It follows that
 .
. -
\({\textsf{Game}_\textsf{1}}\) This game is identical to \(\textsf{Game}_{\textsf{0}}\) except that \(\textsf{O}{\textsf{AggSign}}\) aborts by raising \(\textsf{bad}_\textsf{hcol}\) if on query \((m, \varrho = (h, x))\) it samples a salt \(r\) such that the random oracle \(\textsf{H}\) was already queried at input \(Q = (\textsf{F}^{\star }, m, r, x)\), i.e. \(\textsf{HT}[Q] \ne \bot \). Otherwise it samples
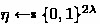 and programs \(\textsf{HT}[Q] \leftarrow \eta \). It follows that
and programs \(\textsf{HT}[Q] \leftarrow \eta \). It follows that
 .
. -
\({\textsf{Game}_\textsf{2}}\) This game is identical to \(\textsf{Game}_{\textsf{1}}\) except that \(\textsf{O}{\textsf{AggSign}}\) aborts by raising \(\textsf{bad}_\textsf{gcol1}\) if on query \((m, \varrho = (h, x))\), after sampling
 it computes \(h' \leftarrow h \oplus \eta \) such that the random oracle \(\textsf{G}\) was already queried at input \(h'\), i.e. \(\textsf{GT}[h'] \ne \bot \). Otherwise it samples
it computes \(h' \leftarrow h \oplus \eta \) such that the random oracle \(\textsf{G}\) was already queried at input \(h'\), i.e. \(\textsf{GT}[h'] \ne \bot \). Otherwise it samples
 and programs \(\textsf{GT}[h'] \leftarrow y' \oplus \alpha \). It follows that
and programs \(\textsf{GT}[h'] \leftarrow y' \oplus \alpha \). It follows that
 .
. -
\({\textsf{Game}_{\textsf{3}}}\) This game is identical to \(\textsf{Game}_{\textsf{2}}\) except that \(\textsf{O}{\textsf{AggSign}}\) directly samples
 , \(x' \leftarrow \textsf{SampDom}(\textsf{F}^{\star })\) and computes \(y' \leftarrow \textsf{F}^{\star }(x')\) instead of computing \(x' \leftarrow \textsf{I}^{\star }(y')\) after sampling
, \(x' \leftarrow \textsf{SampDom}(\textsf{F}^{\star })\) and computes \(y' \leftarrow \textsf{F}^{\star }(x')\) instead of computing \(x' \leftarrow \textsf{I}^{\star }(y')\) after sampling
 . The \(\textrm{PS}\) adversary \(\mathcal {D}\) can simulate both \(\textsf{Game}_{\textsf{2}}\) and \(\textsf{Game}_{\textsf{3}}\), noticing that \(y' = \textsf{F}^{\star }(x')\) and programming \(\textsf{G}\) accordingly. More precisely, on receiving a query \(Q = (m, \varrho = (h, x))\) for \(\textsf{O}{\textsf{AggSign}}\), \(\mathcal {D}\) computes
. The \(\textrm{PS}\) adversary \(\mathcal {D}\) can simulate both \(\textsf{Game}_{\textsf{2}}\) and \(\textsf{Game}_{\textsf{3}}\), noticing that \(y' = \textsf{F}^{\star }(x')\) and programming \(\textsf{G}\) accordingly. More precisely, on receiving a query \(Q = (m, \varrho = (h, x))\) for \(\textsf{O}{\textsf{AggSign}}\), \(\mathcal {D}\) computes
 and programs \(\textsf{GT}[h'] \leftarrow \textsf{F}^{\star }(x') \oplus \alpha \). Both \(\textsf{Game}_{\textsf{2}}\) and \(\textsf{Game}_{\textsf{3}}\) are equivalently modified by moving the programming step of \(\textsf{H}\) and \(\textsf{G}\) to the end of the \(\textsf{O}{\textsf{AggSign}}\). It now follows that when \(\mathcal {D}\) is playing \(\textrm{PS}_0\) its simulation coincides with \(\textsf{Game}_{\textsf{2}}\), while when it is playing \(\textrm{PS}_1\) it coincides with \(\textsf{Game}_{\textsf{3}}\). Either way, \(\mathcal {D}\) simulates the games with at most the same running time of \(\mathcal {A}\) plus the time required for answering the queries to the sampling oracle. The latter takes \(\mathcal {O}\!\!\left( \textsf{poly}\!\!\left( {{\,\textrm{len}\,}}(\mathcal {X}),{{\,\textrm{len}\,}}(\mathcal {Y})\right) \right) \) and is repeated at most \(\textsf{q}_{\textsf{S}}\) times. Finally, we have that
and programs \(\textsf{GT}[h'] \leftarrow \textsf{F}^{\star }(x') \oplus \alpha \). Both \(\textsf{Game}_{\textsf{2}}\) and \(\textsf{Game}_{\textsf{3}}\) are equivalently modified by moving the programming step of \(\textsf{H}\) and \(\textsf{G}\) to the end of the \(\textsf{O}{\textsf{AggSign}}\). It now follows that when \(\mathcal {D}\) is playing \(\textrm{PS}_0\) its simulation coincides with \(\textsf{Game}_{\textsf{2}}\), while when it is playing \(\textrm{PS}_1\) it coincides with \(\textsf{Game}_{\textsf{3}}\). Either way, \(\mathcal {D}\) simulates the games with at most the same running time of \(\mathcal {A}\) plus the time required for answering the queries to the sampling oracle. The latter takes \(\mathcal {O}\!\!\left( \textsf{poly}\!\!\left( {{\,\textrm{len}\,}}(\mathcal {X}),{{\,\textrm{len}\,}}(\mathcal {Y})\right) \right) \) and is repeated at most \(\textsf{q}_{\textsf{S}}\) times. Finally, we have that
 .
. -
\({\textsf{Game}_{\textsf{4}}}\) This game is identical to \(\textsf{Game}_{\textsf{3}}\) except that the random oracle \(\textsf{H}\) is simulated as follows. At the start of the game, the challenger initializes a labeled tree \(\textsf{HTree}\), as described at the beginning of the proof. When \(\textsf{H}\) receives a query \(Q = (\textsf{F}, m, r, x)\), if \(\textsf{HT}[Q] \ne \bot \) it returns it. Otherwise, it samples a uniformly random
 and programs \(\textsf{HT}[Q] \leftarrow \eta \). Then, it checks if Q can be added as a child node of existing nodes in \(\textsf{HTree}\). To determine whether this is the case, it uses the \(\textsf{Lookup}\) function (see Algorithm 3) on input x that checks if it can be tethered to existing nodes, i.e. there exists a node \(N_i \in \textsf{HTree}\) such that \(\textsf{F}_{i}(x) = y_{i}\). If Q can be tethered to more than \(\psi \) nodes, the game aborts by raising \(\textsf{bad}_{\textsf{tcol}}\). Otherwise, \(\textsf{H}\) add a new node \(N_i'\) with parent \(N_i\) for each node \(N_i \in \textsf{HTree}\) returned by \(\textsf{Lookup}(x)\). \(N_i'\) contains the original query Q, the hash response \(\eta \), the hash state \(h_i' \leftarrow h_{i} \oplus \eta \) (where \(h_{i}\) is stored in \(N_{i}\)) and an additional value \(y_i' \leftarrow \textsf{G}(h_i') \oplus \alpha \) (where \(\alpha \) is computed from \(\textsf{enc}(x)\)) that will be used to check if a future node can be tethered via \(\textsf{Lookup}\) queries. It holds that
and programs \(\textsf{HT}[Q] \leftarrow \eta \). Then, it checks if Q can be added as a child node of existing nodes in \(\textsf{HTree}\). To determine whether this is the case, it uses the \(\textsf{Lookup}\) function (see Algorithm 3) on input x that checks if it can be tethered to existing nodes, i.e. there exists a node \(N_i \in \textsf{HTree}\) such that \(\textsf{F}_{i}(x) = y_{i}\). If Q can be tethered to more than \(\psi \) nodes, the game aborts by raising \(\textsf{bad}_{\textsf{tcol}}\). Otherwise, \(\textsf{H}\) add a new node \(N_i'\) with parent \(N_i\) for each node \(N_i \in \textsf{HTree}\) returned by \(\textsf{Lookup}(x)\). \(N_i'\) contains the original query Q, the hash response \(\eta \), the hash state \(h_i' \leftarrow h_{i} \oplus \eta \) (where \(h_{i}\) is stored in \(N_{i}\)) and an additional value \(y_i' \leftarrow \textsf{G}(h_i') \oplus \alpha \) (where \(\alpha \) is computed from \(\textsf{enc}(x)\)) that will be used to check if a future node can be tethered via \(\textsf{Lookup}\) queries. It holds that
 .
. -
\({\textsf{Game}_{\textsf{5}}}\) This game is identical to \(\textsf{Game}_{\textsf{4}}\) except that the random oracle \(\textsf{H}\) is simulated as follows. At the beginning of the game, the challenger uniformly chooses an index
 among the queries to the random oracle \(\textsf{H}\), initializes a counter \(c \leftarrow 0\) and uniformly samples
among the queries to the random oracle \(\textsf{H}\), initializes a counter \(c \leftarrow 0\) and uniformly samples
 . When \(\textsf{H}\) receives a query \(Q = (\textsf{F}, m, r, x)\) it increments \(c \leftarrow c+1\). Then, if \(\textsf{F} = \textsf{F}^{\star }\) and \(c = c^{\star }\) it samples a random index \(i^{\star }\) from the number of nodes in \(\textsf{NList}\). If, for any of the new nodes to be added, it computes \(h_i' \leftarrow h_{i} \oplus \eta \) such that the random oracle \(\textsf{G}\) was already queried at input \(h_i'\), i.e. \(\textsf{GT}[h_i'] \ne \bot \), it aborts by raising \(\textsf{bad}_{\textsf{gcol2}}\). Otherwise, if \(\textsf{F} = \textsf{F}^{\star }\), \(c = c^{\star }\) and \(i = i^{\star }\), it sets \(y_i' \leftarrow y^{\star }\) and programs \(\textsf{GT}[h_i'] \leftarrow y_i' \oplus \alpha \). It holds that
. When \(\textsf{H}\) receives a query \(Q = (\textsf{F}, m, r, x)\) it increments \(c \leftarrow c+1\). Then, if \(\textsf{F} = \textsf{F}^{\star }\) and \(c = c^{\star }\) it samples a random index \(i^{\star }\) from the number of nodes in \(\textsf{NList}\). If, for any of the new nodes to be added, it computes \(h_i' \leftarrow h_{i} \oplus \eta \) such that the random oracle \(\textsf{G}\) was already queried at input \(h_i'\), i.e. \(\textsf{GT}[h_i'] \ne \bot \), it aborts by raising \(\textsf{bad}_{\textsf{gcol2}}\). Otherwise, if \(\textsf{F} = \textsf{F}^{\star }\), \(c = c^{\star }\) and \(i = i^{\star }\), it sets \(y_i' \leftarrow y^{\star }\) and programs \(\textsf{GT}[h_i'] \leftarrow y_i' \oplus \alpha \). It holds that
 .
.

If none of the \(\textsf{bad}\) events happen, \(\mathcal {B}\) perfectly simulate \(\textsf{Game}_{\textsf{5}}\) and we have that

\(\mathcal {B}\) can simulate \(\textsf{Game}_{\textsf{5}}\) with at most the same running time of \(\mathcal {A}\) plus the time required for running \(\textsf{AggVrfy}\) and answering the queries to the random oracles \(\textsf{H}, \textsf{G}\), and to the signing oracle \(\textsf{O}{\textsf{AggSign}}\). These operations takes \(\mathcal {O}\!\!\left( \textsf{poly}\!\!\left( {{\,\textrm{len}\,}}(\mathcal {X}),{{\,\textrm{len}\,}}(\mathcal {Y})\right) \right) \) and are repeated at most \(\textsf{q}_{\textsf{H}}+\textsf{q}_{\textsf{S}}+1\) times.
In the following, we bound the probability of each \(\textsf{bad}\) event happening.
-
Probability of \(\textsf{bad}_{\textsf{hcol}}\) The event \(\textsf{bad}_{\textsf{hcol}}\) occurs on Line 5 of \(\textsf{O}{\textsf{AggSign}}\) on input \((m, \varrho = (h, x))\) when it samples
 such that a value for \(Q = (\textsf{F}^{\star }, m, r, x)\) was already assigned in the \(\textsf{HT}\). The table \(\textsf{HT}\) is populated by either \(\textsf{O}{\textsf{AggSign}}\) or \(\textsf{H}\), so its entries are at most \(\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}}\). The probability that a uniformly random \(r\) produces a collision with one of the entries is then at most \((\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}})2^{-\lambda }\). Since at most \(\textsf{q}_{\textsf{S}}\) are made to \(\textsf{O}{\textsf{AggSign}}\), then \({\text {Pr}}\!\!\left[ \textsf{bad}_\textsf{hcol}\right] \le \textsf{q}_{\textsf{S}}(\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}})2^{-\lambda }\).
such that a value for \(Q = (\textsf{F}^{\star }, m, r, x)\) was already assigned in the \(\textsf{HT}\). The table \(\textsf{HT}\) is populated by either \(\textsf{O}{\textsf{AggSign}}\) or \(\textsf{H}\), so its entries are at most \(\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}}\). The probability that a uniformly random \(r\) produces a collision with one of the entries is then at most \((\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}})2^{-\lambda }\). Since at most \(\textsf{q}_{\textsf{S}}\) are made to \(\textsf{O}{\textsf{AggSign}}\), then \({\text {Pr}}\!\!\left[ \textsf{bad}_\textsf{hcol}\right] \le \textsf{q}_{\textsf{S}}(\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}})2^{-\lambda }\). -
Probability of \({\textsf{bad}_{\textsf{gcol1}}}\) The event \(\textsf{bad}_{\textsf{gcol1}}\) occurs on Line 10 of \(\textsf{O}{\textsf{AggSign}}\) on input \((m, \varrho = (h, x))\) when, after sampling
 , it computes \(h' \leftarrow h \oplus \eta \) such that a value for \(h'\) was already assigned in the \(\textsf{GT}\). The table \(\textsf{GT}\) is populated by either \(\textsf{O}{\textsf{AggSign}}\), \(\textsf{H}\) or \(\textsf{G}\) so its entries are at most \(\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}} + \textsf{q}_{\textsf{G}}\). The probability that a uniformly random \(\eta \) produces a collision with one of the entries is then at most \((\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}} + \textsf{q}_{\textsf{G}})2^{-2\lambda }\). Since at most \(\textsf{q}_{\textsf{S}}\) are made to \(\textsf{O}{\textsf{AggSign}}\), then \({\text {Pr}}\!\!\left[ \textsf{bad}_{\textsf{gcol1}}\right] \le \textsf{q}_{\textsf{S}}(\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}} + \textsf{q}_{\textsf{G}})2^{-2\lambda }\).
, it computes \(h' \leftarrow h \oplus \eta \) such that a value for \(h'\) was already assigned in the \(\textsf{GT}\). The table \(\textsf{GT}\) is populated by either \(\textsf{O}{\textsf{AggSign}}\), \(\textsf{H}\) or \(\textsf{G}\) so its entries are at most \(\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}} + \textsf{q}_{\textsf{G}}\). The probability that a uniformly random \(\eta \) produces a collision with one of the entries is then at most \((\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}} + \textsf{q}_{\textsf{G}})2^{-2\lambda }\). Since at most \(\textsf{q}_{\textsf{S}}\) are made to \(\textsf{O}{\textsf{AggSign}}\), then \({\text {Pr}}\!\!\left[ \textsf{bad}_{\textsf{gcol1}}\right] \le \textsf{q}_{\textsf{S}}(\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}} + \textsf{q}_{\textsf{G}})2^{-2\lambda }\). -
Probability of \(\textsf{bad}_{\textsf{tcol}}\) The event \(\textsf{bad}_{\textsf{tcol}}\) occurs on Line 5 of \(\textsf{Lookup}\) on input x when the \(\textsf{HTree}\) contains \(k > \psi \) nodes \(N_1, \ldots , N_k\) such that \(\textsf{F}_i(x) = y_i\) for \(i=1, \ldots , k\), where \(\textsf{F}_i, y_i\) are stored in their respective nodes \(N_i\). The \(\textsf{HTree}\) is populated by the simulation of the random oracle \(\textsf{H}\). There are at most \(\textsf{q}_{\textsf{H}}\) queries to \(\textsf{H}\) and each query contributes a maximum of \(\psi \) nodes to the tree. Consequently, the total number of nodes in \(\textsf{HTree}\) does not exceed \(\psi \textsf{q}_{\textsf{H}}\). Therefore, we need to bound the probability that any \((\psi +1)\)-tuple of nodes produce a collision on x. To conclude, we prove that for any \((\psi +1)\)-tuple (possibly adversarially chosen) of functions \(\textsf{F}_i :\mathcal {X}\rightarrow \mathcal {Y}\) and uniformly random \(y_i \in \mathcal {Y}\), there exists \(x \in \mathcal {X}\) such that \(\textsf{F}_i(x) = y_i\), for any \(i = 1, \ldots , \psi +1\), with probability at most \(|\mathcal {X}|/|\mathcal {Y}|^{\psi +1}\) (Lemma 3). Indeed, the adversary can issue \(\psi +1\) queries to \(\textsf{H}\) with inputs any functions \(\textsf{F}_i\) to be stored in \(\psi +1\) nodes \(N_i\) in the \(\textsf{HTree}\). However, from Lemma 2, we know that when a new node is added to the \(\textsf{HTree}\) on Line 23 of \(\textsf{H}\), the value \(y_i'\) is chosen uniformly at random from \(\mathcal {Y}\) and is independent of the view of \(\mathcal {A}\). Therefore, the adversary would receive \(\psi +1\) random, independent values \(y_i\). Since the number of \((\psi +1)\)-tuple of nodes in the \(\textsf{HTree}\) are at most \((\psi \textsf{q}_{\textsf{H}})^{\psi +1}/(\psi +1)!\), by the union bound, we obtain \({\text {Pr}}\!\!\left[ \textsf{bad}_{\textsf{tcol}}\right] \le (\psi \textsf{q}_{\textsf{H}})^{\psi +1} |\mathcal {X}|/((\psi +1)! \cdot |\mathcal {Y}|^{\psi +1})\).
-
Probability of \({\textsf{bad}_{\textsf{gcol2}}}\) The event \(\textsf{bad}_{\textsf{gcol2}}\) occurs on Line 16 of \(\textsf{H}\) on input \((\textsf{F}, m, r, x)\) when, after sampling
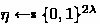 and retrieving \(h_{i-1}\) from the parent node \(N_{i-1}\), it computes \(h_i \leftarrow h_{i-1} \oplus \eta \) such that a value for \(h_i\) was already assigned in the \(\textsf{GT}\). The same argument from the bound of \({\text {Pr}}\!\!\left[ \textsf{bad}_{\textsf{gcol}}\right] \) can be used to prove that \({\text {Pr}}\!\!\left[ \textsf{bad}_\textsf{gcol2}\right] \le \textsf{q}_{\textsf{H}}(\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}} + \textsf{q}_{\textsf{G}})2^{-2\lambda }\).
and retrieving \(h_{i-1}\) from the parent node \(N_{i-1}\), it computes \(h_i \leftarrow h_{i-1} \oplus \eta \) such that a value for \(h_i\) was already assigned in the \(\textsf{GT}\). The same argument from the bound of \({\text {Pr}}\!\!\left[ \textsf{bad}_{\textsf{gcol}}\right] \) can be used to prove that \({\text {Pr}}\!\!\left[ \textsf{bad}_\textsf{gcol2}\right] \le \textsf{q}_{\textsf{H}}(\textsf{q}_{\textsf{S}}' + \textsf{q}_{\textsf{H}} + \textsf{q}_{\textsf{G}})2^{-2\lambda }\). -
Probability of \({\textsf{bad}_\textsf{teth}}\) The event \(\textsf{bad}_\textsf{teth}\) occurs on Line 8 of the simulation of \(\mathcal {B}\) when, after the adversary \(\mathcal {A}\) outputs a valid aggregate signature \(\bar{\varSigma }_n\) for the history \(L_n = (\textsf{pk}_1, m_1), \ldots , (\textsf{pk}_n, m_n)\) the simulator recovers \(x_{i^{\star }}\), with \(i^{\star } \in [n]\) such that \(\textsf{pk}_{i^{\star }} = \textsf{pk}^{\star }\) and \((m_{i^{\star }}, \varsigma _{i^{\star }}) \not \in \mathcal {Q}\), but \(x_{i^{\star }}\) cannot be tethered to any node in the \(\textsf{HTree}\). When \(\textsf{bad}_{\textsf{teth}}\) happens, the aggregate signature \(\bar{\varSigma }_n\) must be valid on \(L_n\). In particular, the inputs \(Q_1 = (\textsf{F}_1, m_1, r_1, \varepsilon ), Q_2 = (\textsf{F}_2, m_2, r_2, x_1), \ldots , Q_{i^{\star }} = (\textsf{F}_{i^{\star }}, m_{i^{\star }}, r_{i^{\star }}, x_{i^{\star }-1})\) have been queried to H in \(\textsf{O}{\textsf{AggVrfy}}\). Let \(\eta _1, \ldots , \eta _{i^{\star }}\) be the outputs of these queries, so that \(\textsf{HT}[Q_j] = \eta _j\). Each of these entries has been populated by \(\textsf{H}\). In fact, the only exception could occur if \((m_{i^{\star }}, x_{i^{\star }-1})\) was queried to \(\textsf{O}{\textsf{AggSign}}\). Suppose \((r, \beta )\) is the complementary part of the signature produced by the oracle as a response. Since the forgery is valid, the complementary part \(\varsigma _{i^{\star }} = (r_{i^{\star }}, \beta _{i^{\star }-1})\) produced by \(\mathcal {A}\) must be different from \((r, \beta )\). However, both \(\beta _{i^{\star }-i}\) and \(\beta \) must be the same partial encoding of \(x_{i^{\star }-1}\), so that \(r_{i^{\star }} \ne r\). Therefore, \(x_{i^{\star }}\) must have been produced following a query to \(\textsf{H}\) with a fresh salt \(r_{i^{\star }}\). Each step of \(\textsf{O}{\textsf{AggVrfy}}\) also recovers a value \(h_j \leftarrow h_{j+1} \oplus \eta _j\) which is the input of the \(\textsf{G}\) query. Since the aggregate signature is correct, we obtain that \(h_1 = \eta _1\). Observe that since \(Q_1\) was queried to \(\textsf{H}\), it must be tethered to the root of \(\textsf{HTree}\) and was therefore inserted as a node of \(\textsf{HTree}\) with additional values \(\eta _1, h_1 = \eta _1, y_1 = \textsf{G}(h_1)\). Then, since \(\textsf{F}(x_1) = y_1\), the query \(Q_2\) is tethered to \(N_1\). Now we prove that either all \(Q_1, \ldots , Q_{i^{\star }}\) are part of a path of nodes in \(\textsf{HTree}\), or there exists an input \(Q_j\) that was queried to \(\textsf{H}\), is tethered to a node in \(\textsf{HTree}\) and is not itself in a node of \(\textsf{HTree}\). We proceed by induction on \(j \le i^{\star }\): we have already shown that \(Q_1\) is in \(\textsf{HTree}\); suppose that \(Q_j\) is in the \(\textsf{HTree}\), then, since \(\textsf{F}_{j}(x_j) = y_j\), the query \(Q_{j+1}\) is tethered to \(Q_j\) and it may or may not be part of \(\textsf{HTree}\). To conclude, we prove that if an input Q has not been entered in the \(\textsf{HTree}\) after being queried to \(\textsf{H}\), the probability that it will ever become tethered to a node in \(\textsf{HTree}\) is at most \(\psi \textsf{q}'/|\mathcal {Y}|\), where \(\textsf{q}'\) is the number of queries made to \(\textsf{H}\) after Q (Lemma 4). Since there are at most \(\textsf{q}_{\textsf{H}}\) queries that add new nodes to \(\textsf{HTree}\), we obtain, by the union bound, that \({\text {Pr}}\!\!\left[ \textsf{bad}_\textsf{teth}\right] \le \psi \textsf{q}_{\textsf{H}}^2/(2|\mathcal {Y}|)\).
Combining the previous bound on \(\textsf{bad}\) events, we obtain the claimed estimate of
 . \(\square \)
. \(\square \)
B Trapdoor Functions in Hash-and-Sign Signature Schemes
1.1 B.1 UOV Trapdoor Function
MQ-based trapdoor function consists of a multivariate quadratic map \(\mathcal {P}:\mathbb {F}_q^n \longrightarrow \mathbb {F}_q^m\) together with a secret information that allows to efficiently find a preimage. For a random map \(\mathcal {P}\), the problem of finding a preimage is called Multivariate Quadratic (MQ) problem. The MQ problem is NP-hard over a finite field. Moreover, it is believed to be hard on average if \(n \sim m\), both classically and quantumly.
Both UOV and MAYO are based on the same trapdoor function. For the description of the trapdoor function we mainly use the formalism introduced by Beullens in [7].
The trapdoor secret information is a linear subspace \(O \subset \mathbb {F}_q^n\) of dimension \(\dim (O) = m\). The trapdoor public function is a homogeneous multivariate quadratic map \(\mathcal {P}:\mathbb {F}_q^n \longrightarrow \mathbb {F}_q^m\) that vanishes on O. For key generation, an m-dimensional subspace \(O \subset \mathbb {F}_q^n\) is randomly chosen, then a multivariate quadratic map \(\mathcal {P}:\mathbb {F}_q^n \longrightarrow \mathbb {F}_q^m\) is randomly chosen such that it vanishes on O. Given a target \(\boldsymbol{{t}} \in \mathbb {F}_q^m\), the secret information O can be used to find a preimage \(\boldsymbol{{s}} \in \mathbb {F}_q^n\), reducing the MQ problem to a linear system. For a map \(\mathcal {P}\), we can define its polar form as \(\mathcal {P}'(\boldsymbol{{x}}, \boldsymbol{{y}}) = \mathcal {P}(\boldsymbol{{x}}+\boldsymbol{{y}}) - \mathcal {P}(\boldsymbol{{x}}) - \mathcal {P}(\boldsymbol{{y}})\). It can be shown that the polar form of a multivariate quadratic map is a symmetric and bilinear map. Now, to find a preimage for \(\boldsymbol{{t}}\), one randomly choose a vector \(\boldsymbol{{v}} \in \mathbb {F}_q^n\) and solves \(\mathcal {P}(\boldsymbol{{v}} + \boldsymbol{{o}}) = \boldsymbol{{t}}\) for \(\boldsymbol{{o}} \in O\). Since
the system reduce to the linear system \(\mathcal {P}^\prime (\boldsymbol{{v}}, \boldsymbol{{o}}) = \boldsymbol{{t}} - \mathcal {P}(\boldsymbol{{v}})\) of m equation and m variables \(\boldsymbol{{o}}\). Notice that whenever the linear map \(\mathcal {P}^\prime (\boldsymbol{{v}}, \cdot )\) is non-singularFootnote 4, the system has a unique solution \(\boldsymbol{{o}} \in O\) and the preimage is \(\boldsymbol{{s}} = \boldsymbol{{v}} + \boldsymbol{{o}}\).
1.2 B.2 Original Unbalanced Oil and Vinegar

Let \(\textsf{T}_{\textrm{uov}} = (\textsf{TrapGen}_{\textrm{uov}}, \textsf{F}_\textrm{uov}, \textsf{I}_\textrm{uov})\) be the TDF based on the description of the previous section. Unbalanced Oil and Vinegar (UOV) [27] is a \(\textsf{HaS}\) signature scheme based on \(\textsf{T}_{\textrm{uov}}\). The key generation and the signing procedure with the trapdoor functions are shown in Algorithm 5.
In the original version of the UOV signature, the signer samples a random salt
 and repeatedly samples
and repeatedly samples
 until there is a solution to the linear system \(\mathcal {P}^\prime (\boldsymbol{{v}}, \boldsymbol{{o}}) = \textsf{H}(m,r) - \mathcal {P}(\boldsymbol{{v}})\). Notice that the UOV signature lies in the \(\textsf{HaS}\) without retry paradigm, therefore \(\textsf{q}_{\textsf{S}}' = \textsf{q}_{\textsf{S}}\) holds in Theorem 1. On the other hand, the \(\textrm{PS}\) advantage term
until there is a solution to the linear system \(\mathcal {P}^\prime (\boldsymbol{{v}}, \boldsymbol{{o}}) = \textsf{H}(m,r) - \mathcal {P}(\boldsymbol{{v}})\). Notice that the UOV signature lies in the \(\textsf{HaS}\) without retry paradigm, therefore \(\textsf{q}_{\textsf{S}}' = \textsf{q}_{\textsf{S}}\) holds in Theorem 1. On the other hand, the \(\textrm{PS}\) advantage term
 cannot be omitted since signature simulation requires knowledge of the trapdoor function.
cannot be omitted since signature simulation requires knowledge of the trapdoor function.
Corollary 1
Let \(\mathcal {A}\) be a strong \(\mathrm {PS\hbox {-}HF\hbox {-}UF\hbox {-}CMA}\) adversary against the \(\mathsf {HaS\hbox {-}HF\hbox {-}SAS}\) scheme on \(\textsf{T}_{\textrm{uov}}\) in the random oracle model, which makes \(\textsf{q}_{\textsf{S}}\) signing queries, \(\textsf{q}_{\textsf{H}}\) queries to the random oracle \(\textsf{H}\) and \(\textsf{q}_{\textsf{G}}\) queries to the random oracle \(\textsf{G}\). Then, there exist a \(\textrm{OW}\) adversary \(\mathcal {B}\) against \(\textsf{T}_{\textrm{uov}}\), and a \(\textrm{PS}\) adversary \(\mathcal {D}\) against \(\textsf{T}_{\textrm{uov}}\) issuing \(\textsf{q}_{\textsf{S}}\) sampling queries, such that

where \(\psi \ge \lceil {{\,\textrm{len}\,}}(\mathcal {X}) / {{\,\textrm{len}\,}}(\mathcal {Y}) \rceil \), and the running time of \(\mathcal {B}\) and \(\mathcal {D}\) are about that of \(\mathcal {A}\).
The previous corollary can be applied to the UOV scheme [10] submitted to the NIST PQC Standardization of Additional Digital Signature. For typical parameters, n is chosen equal to 2.5m. If we choose \(\psi = 3\), the additive error terms in Corollary 1 are negligible for each parametrization in Table 1.
1.3 B.3 Provable Unbalanced Oil and Vinegar

By adopting the probabilistic \(\textsf{HaS}\) with retry paradigm, the UOV signature scheme can be proven \(\mathrm {EUF\hbox {-}CMA}\) secure in the random oracle model [34]. To obtain uniform preimages over \(\mathbb {F}_q^n\), the provable UOV (PUOV) signing procedure is slightly different from the generic one described in Algorithm 1. The signer starts by fixing a random
 , then it repeatedly samples
, then it repeatedly samples
 until there is a solution to the linear system \(\mathcal {P}^\prime (\boldsymbol{{v}}, \boldsymbol{{o}}) = \textsf{H}(m,r) - \mathcal {P}(\boldsymbol{{v}})\). Equivalently, the trapdoor \(\textsf{I}_{\textrm{puov}}\) can be split in two distinct functions \(\textsf{I}_{\textrm{puov}}^1\) and \(\textsf{I}_{\textrm{puov}}^2\). The former is invoked only once and randomly chooses
until there is a solution to the linear system \(\mathcal {P}^\prime (\boldsymbol{{v}}, \boldsymbol{{o}}) = \textsf{H}(m,r) - \mathcal {P}(\boldsymbol{{v}})\). Equivalently, the trapdoor \(\textsf{I}_{\textrm{puov}}\) can be split in two distinct functions \(\textsf{I}_{\textrm{puov}}^1\) and \(\textsf{I}_{\textrm{puov}}^2\). The former is invoked only once and randomly chooses
 . The latter is part of the repeat loop and tries to find a preimage \(\boldsymbol{{s}}\) of the corresponding linear system. The key generation and the signing procedure with the modified trapdoor functions are shown in Algorithm 6.
. The latter is part of the repeat loop and tries to find a preimage \(\boldsymbol{{s}}\) of the corresponding linear system. The key generation and the signing procedure with the modified trapdoor functions are shown in Algorithm 6.
With this procedure, the authors of [34] proved that the preimages produced from \(\textsf{Sign}(\textsf{I}_{\textrm{puov}}, \cdot )\) are indistinguishable from the output of \(\textsf{SampDom}(\textsf{F}_{\textrm{puov}})\), so that in Theorem 1 we have
 .
.
Corollary 2
Let \(\mathcal {A}\) be a strong \(\mathrm {PS\hbox {-}HF\hbox {-}UF\hbox {-}CMA}\) adversary against the \(\mathsf {HaS\hbox {-}HF\hbox {-}SAS}\) scheme on \(\textsf{T}_{\textrm{puov}}\) in the random oracle model, which makes \(\textsf{q}_{\textsf{S}}\) signing queries, \(\textsf{q}_{\textsf{H}}\) queries to the random oracle \(\textsf{H}\) and \(\textsf{q}_{\textsf{G}}\) queries to the random oracle \(\textsf{G}\). Then, there exist a \(\textrm{OW}\) adversary \(\mathcal {B}\) against \(\textsf{T}_{\textrm{puov}}\), such that

where \(\psi \ge \lceil {{\,\textrm{len}\,}}(\mathcal {X}) / {{\,\textrm{len}\,}}(\mathcal {Y}) \rceil \), \(\textsf{q}_{\textsf{S}}'\) is a bound on the total number of queries to \(\textsf{H}\) in all the signing queries, and the running time of \(\mathcal {B}\) is about that of \(\mathcal {A}\).
Unlike Corollary 1, we cannot explicitly take \(\textsf{q}_{\textsf{S}}' = \textsf{q}_{\textsf{S}}\), since in \(\textsf{I}_{\textrm{puov}}^2\) the probability of \(\boldsymbol{{\sigma }} \ne \bot \) depends on the fixed value of \(\boldsymbol{{v}}\) sampled in \(\textsf{I}_{\textrm{puov}}^1\). Depending on the concrete parameters of \(\textsf{T}_{\textrm{puov}}\), we can give a meaningful bound on \(\textsf{q}_{\textsf{S}}'\) so that the probability of having a number of queries to \(\textsf{H}\) greater than \(\textsf{q}_{\textsf{S}}'\) is negligible. \(\textsf{I}_{\textrm{puov}}^2\) returns \(\bot \) on input \((\boldsymbol{{v}}, \boldsymbol{{t}})\) if \(\mathcal {P}'(\boldsymbol{{v}}, \cdot )\) does not have full rank and \(\boldsymbol{{t}} - \mathcal {P}(\boldsymbol{{v}})\) does not belong to the image of \(\mathcal {P}'(\boldsymbol{{v}}, \cdot )\). Let \(\textsf{q}_{ret}\) be a bound for the number of queries to \(\textsf{H}\) each signing query and let \(X_i\) be a random variable on the actual number of queries to \(\textsf{H}\) in the i-th query. Then
As done in [34], we can assume that for a random
 , \(\mathcal {P}'(\boldsymbol{{v}}, \cdot )\) is distributed as a random \(o \times m\) matrix. For \(o \ge m\), the probability that a random \(o \times m\) matrix over \(\mathbb {F}_q\) has rank \(1 \le j \le m\) is given in [29]:
, \(\mathcal {P}'(\boldsymbol{{v}}, \cdot )\) is distributed as a random \(o \times m\) matrix. For \(o \ge m\), the probability that a random \(o \times m\) matrix over \(\mathbb {F}_q\) has rank \(1 \le j \le m\) is given in [29]:
Then, if we choose \(\textsf{q}_{ret}\) such that \(\textsf{q}_{\textsf{S}} {\text {Pr}}\!\!\left[ X_i > \textsf{q}_{ret}\right] \) is negligible, we can use \(\textsf{q}_{\textsf{S}}' = \textsf{q}_{ret} \textsf{q}_{\textsf{S}}\) in the bound of the corollary.
Corollary 2 can be applied to the PROV scheme [26] submitted to the NIST PQC Standardization of Additional Digital Signature. The parameters of PROV are selected so that the dimension of the trapdoor subspace is \(o = m+\delta \). This choice significantly reduces the probability of Eq. (3) whenever \(j < m\). For instance, with the parameters of \(\textsf{PROV}\)-I we have \({\text {Pr}}\!\!\left[ X_i > 1\right] \le 2^{-72}\) and \({\text {Pr}}\!\!\left[ X_i > 2^{14}\right] \le 2^{-160}\). Similarly to Original UOV, if we choose \(\psi = 3\), the additive error terms in Corollary 2 are negligible for each parametrization in [26].
1.4 B.4 MAYO

MAYO [8] is a \(\textsf{HaS}\) signature scheme based on the UOV trapdoor function and employs a so-called whipping technique to use a smaller secret subspace O of dimension \(\dim (O) = o < m\). Let \(\textsf{T}_{\textrm{mayo}} = (\textsf{TrapGen}_{\textrm{mayo}}, \textsf{F}_{\textrm{mayo}}, \textsf{I}_{\textrm{mayo}})\) be the TDF of MAYO. The key generation process is the same as for UOV and produces a multivariate quadratic map \(\mathcal {P}:\mathbb {F}_q^n \rightarrow \mathbb {F}_q^m\) that vanishes on O. In the signing procedure, \(\mathcal {P}\) is deterministically transformed into a larger (whipped) map \(\mathcal {P}^*:\mathbb {F}_q^{kn} \rightarrow \mathbb {F}_q^m\), for some \(k > 1\), which vanishes on \(O^k \subset \mathbb {F}_q^{kn}\) of dimension \(ko \ge m\). In [8], the whipping transformation is obtained by choosing \(k(k+1)/2\) random invertible matrices \(\left\{ \textbf{E}_{i,j} \in {\text {GL}}_m(\mathbb {F}_q)\right\} _{1 \le i \le j \le k}\) and defining
Similarly to UOV, to find a preimage for \(\boldsymbol{{t}} \in \mathbb {F}_q^m\), we randomly choose \(\boldsymbol{{v}}_1, \ldots , \boldsymbol{{v}}_k \in \mathbb {F}_q^{n-m} \times \boldsymbol{{0}}_m\). Then, \(\mathcal {P}^*(\boldsymbol{{v}}_1 + \boldsymbol{{o}}_1, \ldots , \boldsymbol{{v}}_k + \boldsymbol{{o}}_k) = \boldsymbol{{t}}\) is a system of m linear equation in \(ko \ge m\) variables, so it will be solvable with high probability. The key generation and the preimage computation via \(\textsf{I}_{\textrm{mayo}}\) are shown in Algorithm 7.
Instead of computing \(\textsf{Adv}^{\textrm{ps}}_{\textsf{T}_{\textrm{mayo}}}(\mathcal {D})\), we can use the result of [8, Lemma 2] that bounds the probability \(\textsf{B}\) that \(\mathcal {P}^*(\boldsymbol{{v}}_1 + \boldsymbol{{o}}_1, \ldots , \boldsymbol{{v}}_k + \boldsymbol{{o}}_k)\) does not have full rank. It can be shown that if \(\textsf{I}_{\textrm{mayo}}\) has never output \(\bot \), then the preimages produced by \(\textsf{Sign}(\textsf{I}_{\textrm{mayo}}, \cdot )\) are indistinguishable from \(\textsf{SampDom}(\textsf{F}_{\textrm{mayo}})\). Therefore, we can modify the proof of Theorem 1 by introducing a new intermediate game \(\textsf{Game}_{\textsf{2b}}\). This game is identical to \(\textsf{Game}_{\textsf{2}}\) except that \(\textsf{O}{\textsf{AggSign}}\) aborts if \(\textsf{I}_{\textrm{mayo}}\) outputs \(\bot \). Since there are at most \(\textsf{q}_{\textsf{S}}\) queries are made to \(\textsf{O}{\textsf{AggSign}}\), the probability that \(\textsf{Game}_{\textsf{2b}}\) does not abort is at least \(1-\textsf{q}_{\textsf{S}}\textsf{B}\). It follows that \({\text {Pr}}\!\!\left[ \textsf{Game}_{\textsf{2}}(\mathcal {A}) = 1\right] \le \frac{1}{1-\textsf{q}_{\textsf{S}}\textsf{B}}{\text {Pr}}\!\!\left[ \textsf{Game}_{\textsf{2b}}(\mathcal {A}) = 1\right] \). Now, when \(\textsf{Game}_{\textsf{2b}}\) does not abort, the game is indistinguishable from \(\textsf{Game}_{\textsf{3}}\), so that \({\text {Pr}}\!\!\left[ \textsf{Game}_{\textsf{3}}(\mathcal {A}) = 1\right] = {\text {Pr}}\!\!\left[ \textsf{Game}_{\textsf{2b}}(\mathcal {A}) = 1\right] \). The remainder of the proof proceeds as the original. Finally, since MAYO now does not repeat any signature attempts, we can use \(\textsf{q}_{\textsf{S}}' = \textsf{q}_{\textsf{S}}\) in Theorem 1.
Corollary 3
Let \(\mathcal {A}\) be a strong \(\mathrm {PS\hbox {-}HF\hbox {-}UF\hbox {-}CMA}\) adversary against the \(\mathsf {HaS\hbox {-}HF\hbox {-}SAS}\) scheme on \(\textsf{T}_{\textrm{mayo}}\) in the random oracle model, which makes \(\textsf{q}_{\textsf{S}}\) signing queries, \(\textsf{q}_{\textsf{H}}\) queries to the random oracle \(\textsf{H}\) and \(\textsf{q}_{\textsf{G}}\) queries to the random oracle \(\textsf{G}\). Then, there exist a \(\textrm{OW}\) adversary \(\mathcal {B}\) against \(\textsf{T}_{\textrm{mayo}}\), such that

where \(\psi \ge \lceil {{\,\textrm{len}\,}}(\mathcal {X}) / {{\,\textrm{len}\,}}(\mathcal {Y}) \rceil \), and the running time of \(\mathcal {B}\) is about that of \(\mathcal {A}\).
The previous corollary can be applied to the MAYO scheme [9] submitted to the NIST PQC Standardization of Additional Digital Signature. In order to choose appropriate values for \(\psi \), it is necessary to consider the whipped map \(\mathcal {P}^*:\mathbb {F}_q^{kn} \rightarrow \mathbb {F}_q^m\), from which \(\psi \ge \lceil kn/m \rceil \). If we consider the parameter sets in Table 2, we can choose \(\psi \) equal to 13, 7, 14 and 14 for \(\textsf{MAYO}_1, \textsf{MAYO}_2, \textsf{MAYO}_3\) and \(\textsf{MAYO}_5\) respectively, to obtain negligible additive terms in Corollary 3.
1.5 B.5 Wave

Wave [17] is a \(\textsf{HaS}\) signature scheme based on the family of the generalized \((U, U+V)\)-codes. Let \(\textsf{T}_{\textrm{wave}} = (\textsf{TrapGen}_{\textrm{wave}}, \textsf{F}_{\textrm{wave}}, \textsf{I}_{\textrm{wave}})\) be the TDF of Wave. The \(\textrm{OW}\) security of \(\textsf{F}_{\textrm{Wave}}\) is based on the indistinguishability of \((U, U+V)\)-codes from random codes and the Syndrome Decoding (SD) problem. The indistinguishability problem is NP-complete for large finite fields \(\mathbb {F}_q\), while the SD problem is NP-hard for arbitrary finite fields. The trapdoor secret information is a random generalized \((U,U+V)\)-code over \(\mathbb {F}_q\) of length n and dimension \(k = k_U+k_V\), described by its parity check matrix \(\textbf{H}_{\textsf{sk}} \in \mathbb {F}_q^{(n-k) \times n}\), an invertible matrix \(\textbf{S} \in \mathbb {F}_q^{(n-k) \times (n-k)}\) and a permutation matrix \(\textbf{P} \in \mathbb {F}_q^{n \times n}\). Using the underlying structure of the \((U,U+V)\)-code, an efficient decoding algorithm \(D_{\textbf{H}_{\textsf{sk}}}\) is produced. The public function \(\textsf{F}_{\textrm{Wave}}\) is obtained from the parity check matrix \(\textbf{H}_{\textsf{pk}} = \textbf{S}\textbf{H}_{\textsf{sk}}\textbf{P}\). Let \(S_{w,n}\) be the subset of vectors in \(\mathbb {F}_q^n\) with Hamming weight w. The weight w is chosen such that the public function \(\textsf{F}_{\textrm{wave}}:\boldsymbol{{e}} \in S_{w,n} \mapsto \boldsymbol{{e}}\mathbf {\textbf{H}}^\intercal _{\textsf{pk}} \in \mathbb {F}_q^{n-k}\) is a surjection. To find a preimage for \(\boldsymbol{{y}} \in \mathbb {F}_q^{n-k}\), the signer uses the decoding algorithm \(D_{\textbf{H}_{\textsf{sk}}}\) on \(\boldsymbol{{y}}\mathbf {(\textbf{S}^{-1})}^\intercal \) to find \(\boldsymbol{{e}} \in S_{w,n}\), and finally returns \(\boldsymbol{{e}}\textbf{P}\). The key generation and the preimage computation via \(\textsf{I}_{\textrm{wave}}\) are shown in Algorithm 8.
Wave can be described in the \(\textsf{HaS}\) without retry paradigm, therefore \(\textsf{q}_{\textsf{S}}' = \textsf{q}_{\textsf{S}}\) holds in Theorem 1. In [14], \(\textsf{T}_{\textrm{wave}}\) is described in the context of ATPSF, a weaker notion of PSF where the uniformity property on preimages is required to hold only on average. In particular, for any \((\textsf{F}, \textsf{I}) \leftarrow \textsf{TrapGen}_{\textrm{wave}}(1^\lambda )\), consider the statistical distance \(\varepsilon _{\textsf{F}, \textsf{I}} = \varDelta (\textsf{SampDom}(\textsf{F}), \textsf{I}(U(\mathcal {Y})))\). Then, it holds that \(\mathbb {E}_{(\textsf{F}, \textsf{I})}[{\varepsilon _{\textsf{F}, \textsf{I}}}] \le \varepsilon \), where \(\varepsilon \) is negligible in the security parameter \(\lambda \). In Theorem 1 we can use this condition and [14, Prop. 1] to bound the distinguishing advantage on \(\textrm{PS}\) with \(\varepsilon \), obtaining
 .
.
Corollary 4
Let \(\mathcal {A}\) be a strong \(\mathrm {PS\hbox {-}HF\hbox {-}UF\hbox {-}CMA}\) adversary against the \(\mathsf {HaS\hbox {-}HF\hbox {-}SAS}\) scheme on \(\textsf{T}_{\textrm{wave}}\) in the random oracle model, which makes \(\textsf{q}_{\textsf{S}}\) signing queries, \(\textsf{q}_{\textsf{H}}\) queries to the random oracle \(\textsf{H}\) and \(\textsf{q}_{\textsf{G}}\) queries to the random oracle \(\textsf{G}\). Then, there exist a \(\textrm{OW}\) adversary \(\mathcal {B}\) against \(\textsf{T}_{\textrm{wave}}\), such that

where \(\psi \ge \lceil {{\,\textrm{len}\,}}(\mathcal {X}) / {{\,\textrm{len}\,}}(\mathcal {Y}) \rceil \), and the running time of \(\mathcal {B}\) is about that of \(\mathcal {A}\).
In Corollary 4, we can choose \(\psi = 3\) to have negligible additive error terms with respect to the parametrization of Table 3.
C PSF-Based Signatures
In Sect. 4, we briefly discussed the applicability of the \(\mathsf {HaS\hbox {-}HF\hbox {-}SAS}\) scheme to Falcon [33] and PSF-based signatures. In general, lattice-based signatures within the GPV framework [24] require the use of PSF. In this section, we discuss how the construction of Sect. 3 can be modified in the presence of PSF.
Definition 11
A TDF \(\textsf{T} = (\textsf{TrapGen}, \textsf{F}, \textsf{I}, \textsf{SampDom})\) is a Preimage Sampleable Function (PSF) if it satisfies the following properties:
-
1.
\(y \leftarrow \textsf{F}(\textsf{SampDom}(\textsf{F}))\) is uniformly distributed over \(\mathcal {Y}\).
-
2.
\(x \leftarrow \textsf{I}(y)\), with
 , is distributed as \(x \leftarrow \textsf{SampDom}(\textsf{F})\) conditioned on \(\textsf{F}(x) = y\).
, is distributed as \(x \leftarrow \textsf{SampDom}(\textsf{F})\) conditioned on \(\textsf{F}(x) = y\). -
3.
For any \(y \in \mathcal {Y}\), \(\textsf{I}(y)\) always returns \(x \in \mathcal {X}\) such that \(\textsf{F}(x) = y\).
A collision-resistant PSF satisfies the following additional properties:
-
4.
For any \(y \in \mathcal {Y}\), the conditional min-entropy of \(x \leftarrow \textsf{SampDom}(\textsf{F})\) conditioned on \(\textsf{F}(x) = y\) is at least \(\omega (\log \lambda )\).
-
5.
For an adversary \(\mathcal {A}\), the probability of \(\mathcal {A}(\textsf{F})\) returning two distinct \(x, x' \in \mathcal {X}\) such that \(\textsf{F}(x) = \textsf{F}(x')\) is negligible in \(\lambda \).
If we consider a PSF without collision resistance, we can apply Theorem 1 and observe that the distinguishing advantage of the PS adversary is 0. In fact, the PS notion of Definition 5 is a weaker condition for indistinguishability on preimages than property 2 of PSFs. Furthermore, following property 3, the signature associated with the PSF can be described in the \(\textsf{HaS}\) without retry paradigm. As a result, we can modify the proof of Theorem 1 by merging \(\textsf{Game}_{\textsf{2}}\) and \(\textsf{Game}_{\textsf{3}}\), without the need to introduce the PS adversary. Unfortunately, this would not change the tightness of the reduction.
Conversely, if we consider a collision-resistant PSF, we can further modify Theorem 1 to obtain a tighter reduction from collision resistance (CR) to \(\mathrm {PS\hbox {-}HF\hbox {-}UF\hbox {-}CMA}\). In the simulation of \(\textsf{H}\) in Algorithm 3, modify Line 21 by taking a random input \(x' \leftarrow X\), assigning \(y' \leftarrow F^{\star }(x')\) and programming the random oracle \(\textsf{G}\) on input \(h'\) with \(y' \oplus \alpha \). Here the simulation of \(\textsf{G}\) is correct since, from property 1 of PSF, \(y'\) is uniformly distributed in \(\mathcal {Y}\). After the adversary returns a forged aggregate signature, if none of the \(\textsf{bad}\) events happen, the value \(x_{i^{\star }}\), from the forgery, and the value \(x'\), produced by \(\textsf{H}\) and stored in the \(\textsf{HTree}\), constitute a collision for \(F^{\star }\). When the reduction is performed from the \(\textrm{OW}\) game as in the original proof of Theorem 1, the \(\textrm{OW}\) adversary provides its challenge to the \(\mathrm {PS\hbox {-}HF\hbox {-}UF\hbox {-}CMA}\) adversary in one of the \(\textsf{q}_{\textsf{H}}\) queries to the random oracle \(\textsf{H}\). This results in a multiplicative loss of advantage by a factor \(\textsf{q}_{\textsf{H}}\). However, when the reduction is performed as above, the CR adversary can prepare responses that will lead to a collision in each query to \(\textsf{H}\) involving the target public key. As a result, we get a tight reduction with only negligible losses from additive terms.
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Meneghetti, A., Signorini, E. (2024). History-Free Sequential Aggregation of Hash-and-Sign Signatures. In: Oswald, E. (eds) Topics in Cryptology – CT-RSA 2024. CT-RSA 2024. Lecture Notes in Computer Science, vol 14643. Springer, Cham. https://doi.org/10.1007/978-3-031-58868-6_8
Download citation
DOI: https://doi.org/10.1007/978-3-031-58868-6_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-58867-9
Online ISBN: 978-3-031-58868-6
eBook Packages: Computer ScienceComputer Science (R0)





 and stores
and stores  .
.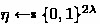 and programs
and programs  .
. it computes
it computes  and programs
and programs  .
. ,
,  . The
. The  and programs
and programs  .
. and programs
and programs  .
. among the queries to the random oracle
among the queries to the random oracle  . When
. When  .
. such that a value for
such that a value for  , it computes
, it computes 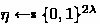 and retrieving
and retrieving  , is distributed as
, is distributed as