Abstract
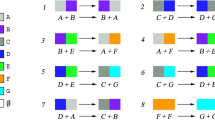
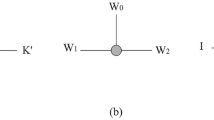
The Chemical Reaction Network (CRN) is a well-studied model that describes the interaction of molecules in well-mixed solutions. In 2014, Qian and Winfree [21] proposed the abstract surface chemical reaction network model (sCRN), which takes advantage of spatial separation by placing molecules on a structured surface, limiting the interaction between molecules. In this model, molecules can only react with their immediate neighbors. Many follow-up works study the computational and pattern-construction power of sCRNs.
In this work, our goal is to describe the power of sCRN by relating the model to other well-studied models in distributed computation. Our main result is to show that, given the same initial configuration, sCRN, affinity-strengthening tile automata, cellular automata, and amoebot can all simulate each other (up to unavoidable rotation and reflection of the pattern). One of our techniques is coloring on-the-fly, which allows all molecules in sCRN to have a global orientation.
This work is supported by NSTC (Taiwan) grant number 110-2223-E-002-006-MY3.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Adleman, L., Cheng, Q., Goel, A., Huang, M.D.: Running time and program size for self-assembled squares. In: Proceedings of the Thirty-Third Annual ACM Symposium on Theory of Computing. p. 740-748 (2001)
Alaniz, R.M., Brunner, J., Coulombe, M., Demaine, E.D., Diomidova, J., Knobel, R., Gomez, T., Grizzell, E., Lynch, J., Rodriguez, A., Schweller, R., Wylie, T.: Complexity of reconfiguration in surface chemical reaction networks (2023)
Alaniz, R.M., Caballero, D., Cirlos, S.C., Gomez, T., Grizzell, E., Rodriguez, A., Schweller, R., Tenorio, A., Wylie, T.: Building squares with optimal state complexity in restricted active self-assembly. J. Comput. Syst. Sci. 138, 103462 (2023)
Alumbaugh, J.C., Daymude, J.J., Demaine, E.D., Patitz, M.J., Richa, A.W.: Simulation of programmable matter systems using active tile-based self-assembly. In: DNA Computing and Molecular Programming. pp. 140–158 (2019)
Angluin, D., Aspnes, J., Fischer, M.J., Jiang, H.: Self-stabilizing population protocols. ACM Trans. Auton. Adapt. Syst. 3(4) (12 2008). https://doi.org/10.1145/1452001.1452003, https://doi.org/10.1145/1452001.1452003
Bhattacharjee, K., Naskar, N., Roy, S., Das, S.: A survey of cellular automata: Types, dynamics, non-uniformity and applications. Natural Computing 19, 433-461 (06 2020)
Brailovskaya, T., Gowri, G., Yu, S., Winfree, E.: Reversible computation using swap reactions on a surface. In: DNA Computing and Molecular Programming. pp. 174–196 (2019)
Caballero, D., Gomez, T., Schweller, R., Wylie, T.: Verification and computation in restricted tile automata. Natural Computing pp. 1–19 (2021)
Chalk, C., Luchsinger, A., Martinez, E., Schweller, R., Winslow, A., Wylie, T.: Freezing simulates non-freezing tile automata. In: DNA Computing and Molecular Programming. pp. 155–172 (2018)
Chen, H.L., Doty, D., Soloveichik, D.: Deterministic function computation with chemical reaction networks. Nat. Comput. 13(4), 517–534 (2014)
Chen, H.L., Doty, D., Soloveichik, D., Reeves, W.: Rate-independent computation in continuous chemical reaction networks. J. ACM 70(3), 1–61 (2023)
Clamons, S., Qian, L., Winfree, E.: Programming and simulating chemical reaction networks on a surface. J. R. Soc. Interface 17, 20190790 (2020)
Cook, M., Soloveichik, D., Winfree, E., Bruck, J.: Programmability of Chemical Reaction Networks, pp. 543–584. Springer Berlin Heidelberg, Berlin, Heidelberg (2009), https://doi.org/10.1007/978-3-540-88869-7_27
Dennunzio, A., Formenti, E., Manzoni, L.: Computing issues of asynchronous ca. Fundam. Inf. 120(2), 165–180 (2012)
Doty, D., Lutz, J.H., Patitz, M.J., Schweller, R.T., Summers, S.M., Woods, D.: The tile assembly model is intrinsically universal. In: IEEE 54th Annual Symposium on Foundations of Computer Science. pp. 302–310 (2012)
Fages, F., Le Guludec, G., Bournez, O., Pouly, A.: Strong turing completeness of continuous chemical reaction networks and compilation of mixed analog-digital programs. In: Feret, J., Koeppl, H. (eds.) Computational Methods in Systems Biology, pp. 108–127. Springer International Publishing, Cham (2017)
Fatès, N., Gerin, L.: Examples of fast and slow convergence of 2d asynchronous cellular systems. In: Cellular Automata. pp. 184–191 (2008)
Hader, D., Patitz, M.J.: The impacts of dimensionality, diffusion, and directedness on intrinsic cross-model simulation in tile-based self-assembly (2023)
von Neumann, J.: Theory of self-reproducing automata (1966), https://cba.mit.edu/events/03.11.ASE/docs/VonNeumann.pdf
Patitz, M.J.: An introduction to tile-based self-assembly. In: Durand-Lose, J., Jonoska, N. (eds.) Unconventional Computation and Natural Computation. pp. 34–62 (2012)
Qian, L., Winfree, E.: Parallel and scalable computation and spatial dynamics with dna-based chemical reaction networks on a surface. In: Murata, S., Kobayashi, S. (eds.) DNA Computing and Molecular Programming, pp. 114–131. Springer International Publishing, Cham (2014)
Rothemund, P., Winfree, E.: The program-size complexity of self-assembled squares. In: Proceedings of the Annual ACM Symposium on Theory of Computing. pp. 459–468 (2000)
Soloveichik, D., Cook, M., Winfree, E., Bruck, J.: Computation with finite stochastic chemical reaction networks. Natural Computing: An International Journal 7(4), 615-633 (dec 2008).https://doi.org/10.1007/s11047-008-9067-y, https://doi.org/10.1007/s11047-008-9067-y
Winfree, E.: Algorithmic self-assembly of dna. In: Proceedings of the International Conference on Microtechnologies in Medicine and Biology. pp. 4–4 (2006)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Lee, YX., Chen, HL. (2024). On the Simulation Power of Surface Chemical Reaction Networks. In: Cho, DJ., Kim, J. (eds) Unconventional Computation and Natural Computation. UCNC 2024. Lecture Notes in Computer Science, vol 14776. Springer, Cham. https://doi.org/10.1007/978-3-031-63742-1_11
Download citation
DOI: https://doi.org/10.1007/978-3-031-63742-1_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-63741-4
Online ISBN: 978-3-031-63742-1
eBook Packages: Computer ScienceComputer Science (R0)