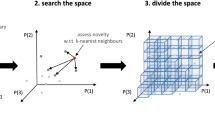
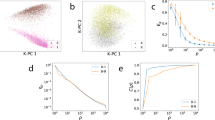
Abstract
Kernel Rank and Generalization Rank are common measures used to characterise reservoir computing systems. However, there are some common issues in literature that make comparisons of these measures difficult, as well as both measures ideally requiring access to the reservoir state. Further, Generalization Rank has an inherent level of arbitrariness in its definition, as well as requiring a separate experiment to compute. This paper introduces the Relative Utilization and Comparative Generalization Measures, as part of the family of Entropy Transformation Measures, which address these issues while capturing similar information.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
A reservoir implementing the identity function would also have a high KR.
References
Allwood, D.A., et al.: A perspective on physical reservoir computing with nanomagnetic devices. Appl. Phys. Lett. 122(4), 040501 (2023)
Büsing, L., Schrauwen, B., Legenstein, R.: Connectivity, dynamics, and memory in reservoir computing with binary and analog neurons. Neural Comput. 22(5), 1272–1311 (2010)
Dale, M., Miller, J.F., Stepney, S., Trefzer, M.A.: A substrate-independent framework to characterize reservoir computers. Proc. Roy. Soc. A 475(2226), 20180723 (2019)
Griffin, D.: Pycharc: Python characterisation of reservoir computers framework (2023). https://github.com/dgdguk/pycharc/
Jaeger, H.: Short term memory in echo state networks. Technical report 152, GMD (2002)
Jaeger, H., Haas, H.: Harnessing nonlinearity: predicting chaotic systems and saving energy in wireless communication. Science 304(5667), 78–80 (2004)
Kullback, S., Leibler, R.A.: On information and sufficiency. Ann. Math. Stat. 22(1), 79–86 (1951)
Love, J., Mulkers, J., Bourianoff, G., Leliaert, J., Everschor-Sitte, K.: Task agnostic metrics for reservoir computing. arXiv:2108.01512v1 [cs.LG] (2021)
Maass, W.: Networks of spiking neurons: the third generation of neural network models. Neural Netw. 10(9), 1659–1671 (1997)
Roy, O., Vetterli, M.: The effective rank: a measure of effective dimensionality. In: 15th European Signal Processing Conference, pp. 606–610. IEEE (2007)
Shannon, C.E.: A mathematical theory of communication. Bell Syst. Tech. J. 27(3), 379–423 (1948)
Spearman, C.: The proof and measurement of association between two things. Am. J. Psychol. 15(1), 72–101 (1904). http://www.jstor.org/stable/1412159
Stewart, G.W.: On the early history of the singular value decomposition. SIAM Rev. 35(4), 551–566 (1993)
Vidamour, I.T., et al.: Quantifying the computational capability of a nanomagnetic reservoir computing platform with emergent magnetisation dynamics. Nanotechnology 33(48), 48520 (2022)
Acknowledgments
The authors acknowledge funding from the MARCH project, EPSRC grant numbers EP/V006029/1 and EP/V006339/1. The authors would like to thank Ian Vidamour for providing details on his implementation of Generalisation Rank.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Griffin, D., Stepney, S. (2024). Entropy Transformation Measures for Computational Capacity. In: Cho, DJ., Kim, J. (eds) Unconventional Computation and Natural Computation. UCNC 2024. Lecture Notes in Computer Science, vol 14776. Springer, Cham. https://doi.org/10.1007/978-3-031-63742-1_9
Download citation
DOI: https://doi.org/10.1007/978-3-031-63742-1_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-63741-4
Online ISBN: 978-3-031-63742-1
eBook Packages: Computer ScienceComputer Science (R0)