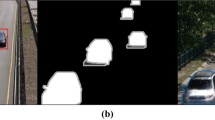
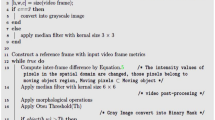
Abstract
This is a follow-up study on Zernike moments applicable in detection tasks owing to a construction of complex-valued integral images that we have proposed in [3]. The main goal of the proposition was to calculate the mentioned features fast (in constant-time). The proposed solution can be applied with success when dealing with single images, however it is still too slow to be used in real-time applications, for example in video processing. In this work we attempted to solve mentioned problem.
In this paper we propose a technique in order to reduce the detection time in real-time applications. The degree of reduction is controlled by two parameters: fs (related to the gap between frames that undergo a full scan) and nb (related to the size of neighborhood to be searched on non-fully scanned frames). We present a series of experiments to show how our solution performs in terms of both detection time and accuracy.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
ZMs expressed by () arise as inner products of the approximated function and Zernike polynomials: \(M_{p,q}=\langle f, V_{p,q}\rangle \big / \Vert V_{p,q}\Vert ^2\).
- 2.
In [3] we have proved that integral images \(ii_{t,u}\) and \(ii_{u,t}\) are complex conjugates at all points, which allows for computational savings.
References
Acasandrei, L., Barriga, A.: Embedded face detection application based on local binary patterns. In: 2014 IEEE International Conference on High Performance Computing and Communications (HPCC,CSS,ICESS), pp. 641–644 (2014)
Aly, S., sayed, A.: An effective human action recognition system based on zernike moment features. In: 2019 International Conference on Innovative Trends in Computer Engineering (ITCE), pp. 52–57 (2019)
Bera, A., Klęsk, P., Sychel, D.: Constant-Time Calculation of Zernike Moments for Detection with Rotational Invariance. IEEE Trans. Pattern Anal. Mach. Intell. 41(3), 537–551 (2019)
de Campos, T.E., et al.: Character recognition in natural images. In: Proceedings of the International Conference on Computer Vision Theory and Applications, Lisbon, Portugal, pp. 273–280 (2009)
Dalal, N., Triggs, B.: Histograms of Oriented Gradients for Human Detection. In: Conference on Computer Vision and Pattern Recognition (CVPR’05) – Vol 1, pp. 886–893. IEEE Computer Society (2005)
Friedman, J., Hastie, T., Tibshirani, R.: Additive logistic regression: a statistical view of boosting. Ann. Stat. 28(2), 337–407 (2000)
Jia, Z., Liao, S.: Leaf recognition using k-nearest neighbors algorithm with zernike moments. In: 2023 8th International Conference on Image, Vision and Computing (ICIVC), pp. 665–669 (2023)
Klęsk, P., Bera, A., Sychel, D.: Reduction of Numerical Errors in Zernike Invariants Computed via Complex-Valued Integral Images. In: Krzhizhanovskaya, V.V., et al. (eds.) ICCS 2020. LNCS, vol. 12139, pp. 327–341. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-50420-5_24
Klęsk, P., Bera, A., Sychel, D.: Extended zernike invariants backed with complex-valued integral images for detection tasks. Proc. Comput. Sci. 192, 357–368 (2021)
Lai, W., et al.: Single-pixel detecting of rotating object using zernike illumination. Opt. Lasers Eng. 172, 107867 (2024)
Liang, X., Ma, W., Zhou, J., Kong, S.: Star identification algorithm based on image normalization and zernike moments. IEEE Access 8, 29228–29237 (2020)
Malek, M.E., Azimifar, Z., Boostani, R.: Facial age estimation using Zernike moments and multi-layer perceptron. In: 22nd International Conference on Digital Signal Processing (DSP), pp. 1–5 (2017)
Mukundan, R., Ramakrishnan, K.: Moment Functions in Image Analysis — Theory and Applications. World Scientific (1998)
Rasolzadeh, B., et al.: Response binning: improved weak classifiers for boosting. In: IEEE Intelligent Vehicles Symposium, pp. 344–349 (2006)
Singh, C., Upneja, R.: Accurate computation of orthogonal Fourier-Mellin moments. J. Math. Imaging Vis. 44(3), 411–431 (2012)
Vengurlekar, S.G., Jadhav, D., Shinde, S.: Object detection and tracking using zernike moment. In: 2019 International Conference on Communication and Electronics Systems (ICCES), pp. 12–17 (2019)
Viola, P., Jones, M.: Rapid Object Detection using a Boosted Cascade of Simple Features. In: Conference on Computer Vision and Pattern Recognition (CVPR’2001), pp. 511–518. IEEE (2001)
Wang, K., Wang, H., Wang, J.: Terrain matching by fusing hog with zernike moments. IEEE Trans. Aerosp. Electron. Syst. 56(2), 1290–1300 (2020)
Xing, M., et al.: Traffic sign detection and recognition using color standardization and Zernike moments. In: 2016 Chinese Control and Decision Conference (CCDC), pp. 5195–5198 (2016)
Zernike, F.: Beugungstheorie des Schneidenverfahrens und seiner verbesserten Form, der Phasenkontrastmethode. Phys. 1(8), 668–704 (1934)
Zheng, N., Zhang, G., Zhang, Y., Sheykhahmad, F.R.: Brain tumor diagnosis based on zernike moments and support vector machine optimized by chaotic arithmetic optimization algorithm. Biomed. Signal Process. Control 82 (2023)
Zhou, Z., Liu, P., Chen, G., Liu, Y.: Moving object detection based on zernike moments. In: 2016 5th International Conference on Computer Science and Network Technology (ICCSNT), pp. 696–699 (2016)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Bera, A., Sychel, D., Klęsk, P. (2024). Rotationally Invariant Object Detection on Video Using Zernike Moments Backed with Integral Images and Frame Skipping Technique. In: Franco, L., de Mulatier, C., Paszynski, M., Krzhizhanovskaya, V.V., Dongarra, J.J., Sloot, P.M.A. (eds) Computational Science – ICCS 2024. ICCS 2024. Lecture Notes in Computer Science, vol 14833. Springer, Cham. https://doi.org/10.1007/978-3-031-63751-3_5
Download citation
DOI: https://doi.org/10.1007/978-3-031-63751-3_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-63753-7
Online ISBN: 978-3-031-63751-3
eBook Packages: Computer ScienceComputer Science (R0)