Abstract
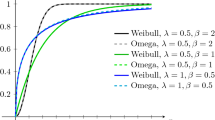
The inclusion of generally distributed random variables in stochastic models is often tackled by choosing a parametric family of distributions and applying fitting algorithms to find appropriate parameters. A recent paper proposed the approximation of probability density functions (PDFs) by Bernstein exponentials, which are obtained from Bernstein polynomials by a change of variable and result in a particular case of acyclic phase-type distributions. In this paper, we show that this approximation can also be applied to cumulative distribution functions (CDFs), which enjoys advantageous properties; by focusing on CDFs, we propose an approach to obtain stochastically ordered approximations.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Aldous, D., Shepp, L.: The least variable phase type distribution is erlang. Stoch. Models 3(3), 467–473 (1987)
Asmussen, S., Nerman, O.: Fitting phase-type distributions via the EM algorithm. In: Proceedings of Symposium i Advent Statistik, Copenhagen, pp. 335–346 (1991)
Baccelli, F., Makowski, A.M.: Multidimensional stochastic ordering and associated random variables. Oper. Res. 37(3), 478–487 (1989)
Bobbio, A., Cumani, A.: ML estimation of the parameters of a PH distribution in triangular canonical form. In: Computer Performance Evaluation, pp. 33–46. Elsevier (1992)
Bobbio, A., Horváth, A., Telek, M.: Matching three moments with minimal acyclic phase type distributions. Stoch. Models 21, 303–326 (2005)
Feldman, A., Whitt, W.: Fitting mixtures of exponentials to long-tail distributions to analyze network performance models. Perform. Eval. 31, 245–279 (1998)
Fourneau, J.M., Pekergin, N.: A numerical analysis of dynamic fault trees based on stochastic bounds. In: Campos, J., Haverkort, B.R. (eds.) QEST 2015. LNCS, vol. 9259, pp. 176–191. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-22264-6_12
Horváth, A., Telek, M.: Approximating heavy tailed behavior with phase-type distributions. In: Proceedings of 3rd International Conference on Matrix-Analytic Methods in Stochastic models, Leuven, Belgium (2000)
Horváth, A., Vicario, E.: Construction of phase type distributions by Bernstein exponentials. In: Iacono, M., Scarpa, M., Barbierato, E., Serrano, S., Cerotti, D., Longo, F. (eds.) EPEW ASMTA 2023. LNCS, vol. 14231, pp. 201–215. Springer, Cham (2023). https://doi.org/10.1007/978-3-031-43185-2_14
Latouche, G., Ramaswami, V.: Introduction to Matrix Analytic Methods in Stochastic Modeling. SIAM (1999)
Neuts, M.: Probability distributions of phase type. In: Liber Amicorum Prof. Emeritus H. Florin, pp. 173–206. University of Louvain (1975)
Neuts, M.F.: Matrix Geometric Solutions in Stochastic Models. Johns Hopkins University Press, Baltimore (1981)
Phillips, G.M.: Interpolation and Approximation by Polynomials. Springer, New York (2003)
Riska, A., Diev, V., Smirni, E.: An EM-based technique for approximating long-tailed data sets with PH distributions. Perform. Eval. 55(1–2), 147–164 (2004)
Rivlin, T.J.: An Introduction to the Approximation of Functions. Courier Corporation (1981)
Telek, M., Horváth, G.: A minimal representation of Markov arrival processes and a moments matching method. Perform. Eval. 64(9–12), 1153–1168 (2007)
Acknowledgments
M. Telek was supported by the OTKA K-138208 project of the Hungarian Scientific Research Fund. E. Vicario was supported bt the RESTART project, as a part of the Italian PNNR programme.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Horváth, A., Horváth, I., Paolieri, M., Telek, M., Vicario, E. (2024). Approximation of Cumulative Distribution Functions by Bernstein Phase-Type Distributions. In: Hillston, J., Soudjani, S., Waga, M. (eds) Quantitative Evaluation of Systems and Formal Modeling and Analysis of Timed Systems. QEST+FORMATS 2024. Lecture Notes in Computer Science, vol 14996. Springer, Cham. https://doi.org/10.1007/978-3-031-68416-6_6
Download citation
DOI: https://doi.org/10.1007/978-3-031-68416-6_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-68415-9
Online ISBN: 978-3-031-68416-6
eBook Packages: Computer ScienceComputer Science (R0)