Abstract
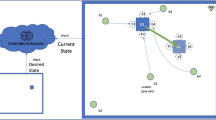
Distributed manipulation systems employ a grid of independently controlled actuators to achieve precise manipulation of objects resting on their surface. Despite the decentralized nature of the actuators, current implementations use centralized feedback mechanisms to provide information about the object’s position to the controllers. This centralized approach introduces a potential vulnerability, as a failure in the feedback system could result in the complete failure of the system. This paper proposes an approach for characterizing objects in decentralized systems. Its validation is demonstrated through the implementation of a two-dimensional simulated network of sensing agents. These agents work collaboratively to determine a global property - the geometrical center of an object - through local communication of the information at their disposal. The method uses a Neural Cellular Automaton, a multi-agent system in which the update rule of each agent is expressed as a Neural Network, and it is a function of its neighborhood’s information. Experiments show that trained on known objects, the system displayed outstanding precision in inferring their centers and demonstrated remarkable adaptability when encountering unknown objects.
Funded by the European Union. Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the granting authority can be held responsible for them.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Based on [5] and Included for Completeness.
References
Adamatzky, A.: Game of Life Cellular Automata. Springer, London (2010)
Agarwal, P.K., Kavraki, L.E., Mason, M.T.: Velocity field design for the modular distributed manipulator system (MDMS). In: Robotics: The Algorithmic Perspective, pp. 45–58. A K Peters/CRC Press (1998)
Bedillion, M.D., Parajuli, D., Hoover, R.C.: Distributed sensing in actuator array manipulation. In: Volume 4A: Dynamics, Vibration and Control, p. V04AT04A002. American Society of Mechanical Engineers, San Diego, California, USA (2013). https://doi.org/10.1115/IMECE2013-62499
Bessone, N.: NCA for Decentralized Inference (2024). https://github.com/nhbess/Neural-Cellular-Automaton-for-Decentralized-Inference-in-Distributed-Manipulator-Systems
Bessone, N., Zahadat, P., Stoy, K.: Decentralized control of distributed manipulators: an information diffusion approach. In: Proceedings of the 23rd International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2024), p. 3. Auckland, New Zealand, May 6–10, 2024, IFAAMAS (2024). (In press)
Gilpin, W.: Cellular automata as convolutional neural networks. Phys. Rev. E 100(3) (2019). https://doi.org/10.1103/PhysRevE.100.032402
Ha, D., Tang, Y.: Collective intelligence for deep learning: a survey of recent developments (2022)
Luntz, J.E., Messner, W., Choset, H.: Distributed manipulation using discrete actuator arrays. Int. J. Robot. Res. 20(7), 553–583 (2001). https://doi.org/10.1177/02783640122067543
Mordvintsev, A., Randazzo, E., Niklasson, E., Levin, M.: Growing neural cellular automata. Distill (2020). https://doi.org/10.23915/distill.00023
Murphey, T.D., Burdick, J.W.: Feedback control methods for distributed manipulation systems that involve mechanical contacts. Int. J. Robot. Res. 23, 763–781 (2004). https://doi.org/10.1177/0278364904045480
Nadizar, G., Medvet, E., Walker, K., Risi, S.: A fully-distributed shape-aware neural controller for modular robots. In: Proceedings of the Genetic and Evolutionary Computation Conference. pp. 184–192. ACM, Lisbon Portugal (2023). https://doi.org/10.1145/3583131.3590419
Parajuli, D., Bedillion, M.D., Hoover, R.C.: Actuator array manipulation using low resolution local sensing. In: Volume 4A: Dynamics, Vibration, and Control. p. V04AT04A003. American Society of Mechanical Engineers, Montreal, Quebec, Canada (2014). https://doi.org/10.1115/IMECE2014-37147
Randazzo, E., Mordvintsev, A., Niklasson, E., Levin, M., Greydanus, S.: Self-classifying MNIST digits. Distill (2020). https://doi.org/10.23915/distill.00027.002
Walker, K., Palm, R.B., Moreno, R., Faina, A., Stoy, K., Risi, S.: Physical neural cellular automata for 2D shape classification. In: 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 12667–12673. IEEE, Kyoto, Japan (2022). https://doi.org/10.1109/IROS47612.2022.9981214, https://ieeexplore.ieee.org/document/9981214/
Wolfram, S.: The problem of distributed consensus: a survey. arXiv preprint arXiv:2106.13591 (2021)
Wulff, N., Hertz, J.A.: Learning cellular automaton dynamics with neural networks. In: Advances in Neural Information Processing Systems. vol. 5. Morgan-Kaufmann (1992)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2025 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Bessone, N., Zahadat, P., Stoy, K. (2025). Neural Cellular Automaton for Decentralized Inference in Distributed Manipulation Systems. In: Mathieu, P., De la Prieta, F. (eds) Advances in Practical Applications of Agents, Multi-Agent Systems, and Digital Twins: The PAAMS Collection. PAAMS 2024. Lecture Notes in Computer Science(), vol 15157. Springer, Cham. https://doi.org/10.1007/978-3-031-70415-4_6
Download citation
DOI: https://doi.org/10.1007/978-3-031-70415-4_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-70414-7
Online ISBN: 978-3-031-70415-4
eBook Packages: Computer ScienceComputer Science (R0)