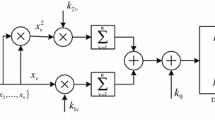
Abstract
The paper analyzes the development of innovative models and methods for detecting and distinguishing signals in non-Gaussian noise. The authors propose a new quality criterion for statistical hypothesis testing, based on describing the random process through its moments. The paper suggests the use of stochastic polynomials to develop decision rules, where the optimal coefficients are determined by the new adapted moment quality criterion for multiple hypothesis testing. The paper provides an analysis of the synthesized models and polynomial algorithms used for detecting and distinguishing signals in non-Gaussian noise. A generalized structure of polynomial decision rules for multiple statistical hypothesis testing is suggested. The paper highlight the fact that nonlinear processing of samples, considering parameters of non-Gaussian distribution of random variables such as moments of the third and higher orders, can improve signal processing efficiency. This paper also explores the development of effective methods and algorithms for processing data in non-Gaussian noise. Research has demonstrated that the enhanced effectiveness of nonlinear signal processing, relative to existing results, is contingent upon accounting for the characteristics of non-Gaussian noise.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Hautus, M.J., Macmillan, N.A., Creelman, C.D.: Detection Theory: A User's Guide, 3rd edn. Routledge (2021). https://doi.org/10.4324/9781003203636
Van Trees, H.L., Bell, K. L., Tiany, Z.: Detection Estimation and Modulation Theory, 2nd edn., Part I, Detection, Estimation, and Filtering Theory. John Wiley & Sons (2013)
Kay, S.M.: Fundamentals of Statistical Signal Processing. Prentice Hall PTR, NJ (2008)
Kassam, S.: Signal Detection in Non-Gaussian Noise. Springer Verlag, New York (2011)
Zhang, X.-D.: Modern Signal Processing. Tsinghua University Press (2023)
Duana, F., Chapeau-Blondeaub, F., Abbott, D.: Non-Gaussian noise benefits for coherent detection of narrow band weak signal. Phys. Lett. A 378, 1820–1824 (2014)
Tang, M., Rong, Y., De Maio, A., Chen, C., Zhou, J.: Adaptive radar detection in Gaussian disturbance with structured covariance matrix via invariance theory. IEEE Trans. Signal Process. 67(21), 5671–5685 (2019)
Picinbono, B., Duvant, P.: Optimal linear-quadratic systems for detection and estimation. IEEE Trans. Inf. Theory 34(2), 304–311 (1988)
Chevalier, P., Picinbono, B.: Complex linear-quadratic systems for detection and array processing. IEEE Trans. Sig. Process. 44(10), 2631–2634 (1996)
Rousseau, D., Anand, G.V., Chapeau-Blondeau, F.: Noise–enhanced nonlinear detector to improve signal detection in non–Gaussian noise. IEEE Signal Process. 86(11), 3456–3465 (2006)
Coulon, M., Tourneret, J.-Y., Swami, A.: Detection of multiplicative noise in stationary random processes using second- and higher order statistics. IEEE Trans. Signal Process. 48(9), 2566–2575 (2000)
Denkovski, D., Atanasovski, V., Gavrilovska, L.: HOS based goodness-of-fit testing signal detection. IEEE Commun. Lett. 16(3), 310–313 (2012)
Malakhov, A.: Cumulant analysis of non-Gaussian processes and their transformation. Sovetskoe Radio (1979)
Kunchenko, Y.: Polynomial Parameter Estimations of Close to Gaussian Random Variables. Shaker Verlag, Aachen (2002)
Kunchenko, Y.: A moment performance criterions of a deccision-making for testing simple statistical conjecture. In: ISIT 1997, Ulm, Germany, 29 June–4 July, p. 407 (1997)
Vokorokos, L., Marchevsky, S., Ivchenko, A., Palahina, E., Palahin, V.: Parameters estimation of correlated non-Gaussian processes by the method of polynomial maximization. 11(3), 313–319 (2017). https://doi.org/10.1049/iet-spr.2016.0142
Palahin, V., Juhar, J., Leleko, S., Polozhaenko, S., Palahina, E.: Computer simulation of signal detection in non-Gaussian noise with the Neyman-Pearson moment quality criterion. In: Proceedings of the 9th International IEEE Conference Dependable Systems, Services and Technologies DESSERT 2018, pp. 639–644 (2018). https://doi.org/10.1109/DESSERT.2018.8409203
Palahin, V., Honcharov, A., Umanets, V.: Computer simulation of polynomial algorithms of radio signals distinction and estimating their parameters. Eastern-Eur. J. Enterp. Technol. 5(9), 31–39 (2014)
Palahin, V., Juhar, Zorin, O., Viediernikov, D., Palahina, E.: Computer modeling of noise signals processing system in non-Gaussian noise. In: IEEE 38th International Conference on Electronics and Nanotechnology (ELNANO-2018), Kiev, pp.658–662 (2018)
Smirnov, D., Palahina, E., Palahin, V.: Mathematical modeling of signal detection in non-gaussian correlated noise. In: Arsenyeva, O., Romanova, T., Sukhonos, M., Tsegelnyk, Y. (eds.) Smart Technologies in Urban Engineering. STUE 2022. Lecture Notes in Networks and Systems, vol. 536, pp. 65–74. Springer, Cham (2023). https://doi.org/10.1007/978-3-031-20141-7_7
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Smirnov, D., Zorin, O., Palahina, E., Ivchenko, O., Palahin, V. (2024). Development of Moment Quality Criterion and Polynomial Methods for Signals Detection and Distinction in Non-Gaussian Noise. In: Faure, E., et al. Information Technology for Education, Science, and Technics. ITEST 2024. Lecture Notes on Data Engineering and Communications Technologies, vol 221. Springer, Cham. https://doi.org/10.1007/978-3-031-71801-4_27
Download citation
DOI: https://doi.org/10.1007/978-3-031-71801-4_27
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-71800-7
Online ISBN: 978-3-031-71801-4
eBook Packages: EngineeringEngineering (R0)