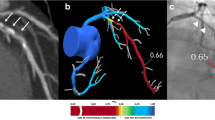
Abstract
Fractional flow reserve evaluation plays a crucial role in diagnosing ischemic coronary artery disease. Machine learning based fractional flow reserve evaluation has become the most important method due to it effectiveness and high computation efficiency. However, it still suffers from lacking of the proper description for the coronary artery fluid. This study presents a variational field constraint learning method for assessing fractional flow reserve from digital subtraction angiography images. Our method offers a promising approach by integrating governing equations and boundary conditions as unified constraints. By leveraging a holistic consideration of the fluid dynamics, our method achieves more accurate fractional flow reserve prediction compared to existing methods.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Yuehua Li, Mengmeng Yu, Xu Dai, Zhigang Lu, Chengxing Shen, Yining Wang, Bin Lu, and Jiayin Zhang. Detection of hemodynamically significant coronary stenosis: Ct myocardial perfusion versus machine learning ct fractional flow reserve. Radiology, 293(2):305–314, 2019.
Zhifan Gao, Xin Wang, Shanhui Sun, Dan Wu, Junjie Bai, Youbing Yin, Xin Liu, Heye Zhang, and Victor Hugo C de Albuquerque. Learning physical properties in complex visual scenes: An intelligent machine for perceiving blood flow dynamics from static ct angiography imaging. Neural Networks, 123:82–93, 2020.
PIJLS NH. Fractional flow reserve: A useful index to evaluate the influence of an epicardial coronary stenosis on myocardial blood flow. Circulation, 92:3183–3193, 1995.
Bernard de Bruyne, Jozef Bartunek, Stanislas U Sys, Nico HJ Pijls, Guy R Heyndrickx, and William Wijns. Simultaneous coronary pressure and flow velocity measurements in humans: feasibility, reproducibility, and hemodynamic dependence of coronary flow velocity reserve, hyperemic flow versus pressure slope index, and fractional flow reserve. Circulation, 94(8):1842–1849, 1996.
Nico HJ Pijls, William F Fearon, Pim AL Tonino, Uwe Siebert, Fumiaki Ikeno, Bernhard Bornschein, Marcel van’t Veer, Volker Klauss, Ganesh Manoharan, Thomas Engstrøm, et al. Fractional flow reserve versus angiography for guiding percutaneous coronary intervention in patients with multivessel coronary artery disease: 2-year follow-up of the fame (fractional flow reserve versus angiography for multivessel evaluation) study. Journal of the American College of Cardiology, 56(3):177–184, 2010.
Baihong Xie, Xiujian Liu, Heye Zhang, Chenchu Xu, Tieyong Zeng, Yixuan Yuan, Guang Yang, and Zhifan Gao. Conditional physics-informed graph neural network for fractional flow reserve assessment. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 110–120. Springer, 2023.
Charles A Taylor, Kersten Petersen, Nan Xiao, Matthew Sinclair, Ying Bai, Sabrina R Lynch, Adam UpdePac, and Michiel Schaap. Patient-specific modeling of blood flow in the coronary arteries. Computer Methods in Applied Mechanics and Engineering, 417:116414, 2023.
Christian Tesche, Carlo N De Cecco, Stefan Baumann, Matthias Renker, Tindal W McLaurin, Taylor M Duguay, Richard R Bayer 2nd, Daniel H Steinberg, Katharine L Grant, Christian Canstein, et al. Coronary ct angiography–derived fractional flow reserve: machine learning algorithm versus computational fluid dynamics modeling. Radiology, 288(1):64–72, 2018.
Leonardo Chirco and Sandro Manservisi. An adjoint based pressure boundary optimal control approach for fluid-structure interaction problems. Computers & Fluids, 182:118–127, 2019.
Hyeonyong Hae, Soo-Jin Kang, Won-Jang Kim, So-Yeon Choi, June-Goo Lee, Youngoh Bae, Hyungjoo Cho, Dong Hyun Yang, Joon-Won Kang, Tae-Hwan Lim, et al. Machine learning assessment of myocardial ischemia using angiography: Development and retrospective validation. Plos Medicine, 15(11):e1002693, 2018.
Sifan Wang, Hanwen Wang, and Paris Perdikaris. Learning the solution operator of parametric partial differential equations with physics-informed deeponets. Science Advances, 7(40):eabi8605, 2021.
Georgios Kissas, Yibo Yang, Eileen Hwuang, Walter R Witschey, John A Detre, and Paris Perdikaris. Machine learning in cardiovascular flows modeling: Predicting arterial blood pressure from non-invasive 4d flow mri data using physics-informed neural networks. Computer Methods in Applied Mechanics and Engineering, 358:112623, 2020.
Xuelan Zhang, Baoyan Mao, Yue Che, Jiaheng Kang, Mingyao Luo, Aike Qiao, Youjun Liu, Hitomi Anzai, Makoto Ohta, Yuting Guo, et al. Physics-informed neural networks (pinns) for 4d hemodynamics prediction: An investigation of optimal framework based on vascular morphology. Computers in Biology and Medicine, 164:107287, 2023.
Mohammad Sarabian, Hessam Babaee, and Kaveh Laksari. Physics-informed neural networks for brain hemodynamic predictions using medical imaging. IEEE Transactions on Medical Imaging, 41(9):2285–2303, 2022.
Nadim Saad, Gaurav Gupta, Shima Alizadeh, and Danielle C Maddix. Guiding continuous operator learning through physics-based boundary constraints. arXiv preprint arXiv:2212.07477
Henrik Rosenberger and Benjamin Sanderse. No pressure? energy-consistent roms for the incompressible navier-stokes equations with time-dependent boundary conditions. Journal of Computational Physics, 491:112405, 2023.
Luca Pegolotti, Martin R Pfaller, Alison L Marsden, and Simone Deparis. Model order reduction of flow based on a modular geometrical approximation of blood vessels. Computer Methods in Applied Mechanics and Engineering, 380:113762, 2021.
Martin R Pfaller, Jonathan Pham, Aekaansh Verma, Luca Pegolotti, Nathan M Wilson, David W Parker, Weiguang Yang, and Alison L Marsden. Automated generation of 0d and 1d reduced-order models of patient-specific blood flow. International Journal for Numerical Methods in Biomedical Engineering, 38(10):e3639, 2022.
Qi Zhang, Yahui Zhang, Liling Hao, Yujia Zhong, Kunlin Wu, Zhuo Wang, Shuai Tian, Qi Lin, and Guifu Wu. A personalized 0d-1d model of cardiovascular system for the hemodynamic simulation of enhanced external counterpulsation. Computer Methods and Programs in Biomedicine, 227:107224, 2022.
Cheong-Ah Lee, Hafiz Muhammad Umer Farooqi, and Dong-Guk Paeng. Axial shear rate: A hemorheological factor for erythrocyte aggregation under womersley flow in an elastic vessel based on numerical simulation. Computers in Biology and Medicine, 157:106767, 2023.
Umberto Morbiducci, Raffaele Ponzini, Diego Gallo, Cristina Bignardi, and Giovanna Rizzo. Inflow boundary conditions for image-based computational hemodynamics: impact of idealized versus measured velocity profiles in the human aorta. Journal of Biomechanics, 46(1):102–109, 2013.
Luca Pegolotti, Martin R Pfaller, Alison L Marsden, and Simone Deparis. Model order reduction of flow based on a modular geometrical approximation of blood vessels. Computer Methods in Applied Mechanics and Engineering, 380:113762, 2021.
H Huang and F Costanzo. On the use of space–time finite elements in the solution of elasto-dynamic problems with strain discontinuities. Computer Methods in Applied Mechanics and Engineering, 191(46):5315–5343, 2002.
Paul D Morris, Andrew Narracott, Hendrik von Tengg-Kobligk, Daniel Alejandro Silva Soto, Sarah Hsiao, Angela Lungu, Paul Evans, Neil W Bressloff, Patricia V Lawford, D Rodney Hose, et al. Computational fluid dynamics modelling in cardiovascular medicine. Heart, 102(1):18–28, 2016.
Acknowledgments
This work was supported in part by The National Key Research and Development Program of China (2022YFE0209800), Shenzhen Science and Technology Program (GJHZ20220913142601003), National Natural Science Foundation of China (62101606, 62276282, 62101610, 62325113, 62271511), Guangdong Basic and Applied Basic Research Foundation (2024B1515020062, 2022A1515011384).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Ethics declarations
Disclosure of Interests
The authors have no competing interests to declare that are relevant to the content of this article.
Rights and permissions
Copyright information
© 2024 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Zhang, Q. et al. (2024). Variational Field Constraint Learning for Degree of Coronary Artery Ischemia Assessment. In: Linguraru, M.G., et al. Medical Image Computing and Computer Assisted Intervention – MICCAI 2024. MICCAI 2024. Lecture Notes in Computer Science, vol 15003. Springer, Cham. https://doi.org/10.1007/978-3-031-72384-1_72
Download citation
DOI: https://doi.org/10.1007/978-3-031-72384-1_72
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-72383-4
Online ISBN: 978-3-031-72384-1
eBook Packages: Computer ScienceComputer Science (R0)