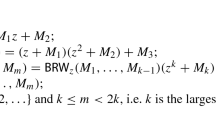Abstract
CGL hash function is an isogeny-based hash function that computes non-backtracking paths on a supersingular isogeny graph. Since one of the problems of CGL hash function is its relatively slow computational time, many acceleration methods have been studied, including the use of Legendre form, radical isogenies. An algorithm for computing CGL hash functions proposed at SAC’22 has achieved acceleration of several orders of magnitude, by using \(2^n\)-isogeny for an integer \(n = \varTheta (\log p)\), where p is characteristic of the underlying field. In the algorithm, the backtracking 2-isogeny between two consecutive \(2^n\)-isogenies must be prevented to assure the security of the hash function.
In this paper, we propose a faster algorithm for CGL hash function by reducing the overhead of the backtracking check in the method at SAC’22. Moreover, as no explicit implementation of the aforementioned algorithm exists to the best of our knowledge, we implement the algorithm with our proposed backtracking check. We conduct a detailed and precise complexity analysis of the algorithm and other previously proposed ones, by programmatically counting the actual number of operations over the underlying finite field. We demonstrate that the proposed algorithm reduces the cost by \(7.6\%\) compared to the original algorithm with 256-bit prime, achieving the fastest computation of CGL hash functions.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Adj, G., Rodríguez-Henríquez, F.: Square root computation over even extension fields. IEEE Trans. Comput. 63(11), 2829–2841 (2014). https://doi.org/10.1109/TC.2013.145
Arpin, S., Camacho-Navarro, C., Lauter, K., Lim, J., Nelson, K., Scholl, T.: Adventures in supersingularland. Exp. Math. 32(2), 241–268 (2021). https://doi.org/10.1080/10586458.2021.1926009
Castryck, W., Decru, T.: An efficient key recovery attack on SIDH. In: Hazay, C., Stam, M. (eds.) EUROCRYPT 2023. LNCS, vol. 14008, pp. 423–447. Springer, Cham (2023). https://doi.org/10.1007/978-3-031-30589-4_15
Castryck, W., Decru, T., Houben, M., Vercauteren, F.: Horizontal racewalking using radical isogenies. In: Agrawal, S., Lin, D. (eds.) ASIACRYPT 2022. LNCS, vol. 13792, pp. 67–96. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-22966-4_3
Castryck, W., Decru, T., Vercauteren, F.: Radical isogenies. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020. LNCS, vol. 12492, pp. 493–519. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64834-3_17
Castryck, W., Lange, T., Martindale, C., Panny, L., Renes, J.: CSIDH: an efficient post-quantum commutative group action. In: Peyrin, T., Galbraith, S. (eds.) ASIACRYPT 2018. LNCS, vol. 11274, pp. 395–427. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03332-3_15
Charles, D.X., Lauter, K.E., Goren, E.Z.: Cryptographic hash functions from expander graphs. J. Crypt. 22(1), 93–113 (2009). https://doi.org/10.1007/s00145-007-9002-x
Costello, C., Longa, P., Naehrig, M.: Efficient algorithms for supersingular isogeny Diffie-Hellman. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 572–601. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_21
Couveignes, J.M.: Hard homogeneous spaces. Cryptology ePrint Archive, Paper 2006/291 (2006). https://eprint.iacr.org/2006/291
De Feo, L., Jao, D., Plût, J.: Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies. J. Math. Cryptol. 8(3), 209–247 (2014). https://doi.org/10.1515/jmc-2012-0015
Doliskani, J., Pereira, G.C.C.F., Barreto, P.S.L.M.: Faster cryptographic hash function from supersingular isogeny graphs. In: Smith, B., Wu, H. (eds.) SAC 2022. LNCS, vol. 13742, pp. 399–415. Springer, Cham (2024). https://doi.org/10.1007/978-3-031-58411-4_18
Hashimoto, Y., Nuida, K.: Efficient construction of CGL hash function using Legendre curves. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. E106.A(9), 1131–1140 (2023). https://doi.org/10.1587/transfun.2022DMP0003
Jao, D., De Feo, L.: Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies. In: Yang, B.-Y. (ed.) PQCrypto 2011. LNCS, vol. 7071, pp. 19–34. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25405-5_2
Maddock, J., Kormanyos, C.: Boost multiprecision library. https://github.com/boostorg/multiprecision
Maino, L., Martindale, C., Panny, L., Pope, G., Wesolowski, B.: A direct key recovery attack on SIDH. In: Hazay, C., Stam, M. (eds.) EUROCRYPT 2023. LNCS, vol. 14008, pp. 448–471. Springer, Cham (2023). https://doi.org/10.1007/978-3-031-30589-4_16
Montgomery, P.L.: Speeding the Pollard and elliptic curve methods of factorization. Math. Comput. 48, 243–264 (1987). https://doi.org/10.1090/S0025-5718-1987-0866113-7
Pereira, G., Doliskani, J., Jao, D.: X-only point addition formula and faster compressed SIKE. J. Cryptogr. Eng. 11, 57–69 (2021). https://doi.org/10.1007/s13389-020-00245-4
Pizer, A.K.: Ramanujan graphs and Hecke operators. Bull. (New Series) Am. Math. Soc. 23(1), 127–137 (1990). https://doi.org/10.1090/S0273-0979-1990-15918-X
Pizer, A.K.: Ramanujan graphs. AMS/IP Stud. Adv. Math. 7, 159–178 (1998)
Pollard, J.: Monte Carlo methods for index compuation mod p. Math. Comput. 32(143), 918–924 (1978). https://doi.org/10.2307/2006496
Robert, D.: Breaking SIDH in polynomial time. In: Hazay, C., Stam, M. (eds.) EUROCRYPT 2023. LNCS, vol. 14008, pp. 472–503. Springer, Cham (2023). https://doi.org/10.1007/978-3-031-30589-4_17
Rostovtsev, A., Stolbunov, A.: Public-key cryptosystem based on isogenies. Cryptology ePrint Archive, Paper 2006/145 (2006). https://eprint.iacr.org/2006/145
Silverman, J.H.: The Arithmetic of Elliptic Curves, 2nd edn. Springer, New York (2009). https://doi.org/10.1007/978-0-387-09494-6
Vélu, J.: Isogenies entre courbes elliptiques. Compets-Rendus de l’Academie des Sciences Serie I 273, 238–241 (1971)
Washington, L.C.: Elliptic Curves: Number Theory and Cryptography, 2nd edn. Chapman & Hall/CRC (2008). https://doi.org/10.1201/9781420071474
Yoshida, R., Takashima, K.: Computing a sequence of 2-isogenies on supersingular elliptic curves. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. E96.A(1), 158–165 (2013). https://doi.org/10.1587/transfun.E96.A.158
Zanon, G.H.M., Simplicio, M.A., Pereira, G.C.C.F., Doliskani, J., Barreto, P.S.L.M.: Faster isogeny-based compressed key agreement. In: Lange, T., Steinwandt, R. (eds.) PQCrypto 2018. LNCS, vol. 10786, pp. 248–268. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-79063-3_12
Acknowledgement
This work was supported by JST CREST Grant Number JPMJCR2113 and JSPS KAKENHI Grant Number 24K20771, Japan.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Appendix
A Appendix
1.1 A.1 Collision Finding for DPB Method Without the Backtracking Check
We show that the backtracking check in DPB method is necessary to be collision-resistant. When the backtracking check is removed, DPB method can compute backtracking paths, which corresponds to non-cyclic isogenies. Thus, the collision-resistance of DPB method is not reduced to Problem 2.
Actually, we can show a polynomial time collision-finding algorithm for DPB method without the backtracking check. The strategy is shown in Fig. 1. We assume that n is even. We can compute \(m,m_0,m_1\in [0,2^n)\) such that \(h(m) = h(m_0 || m_1)\), where h is the hash function and || is the concatenation. Let \(\{P_0, Q_0\} \subset E_0[2^n]\) be a basis of \(E_0[2^n]\), \(E_1\) be \(E_0/\langle P_0 + m_0Q_0 \rangle \), and \(\{P_1, Q_1\} \subset E_1[2^n]\) be a basis of \(E_1[2^n]\). The collision pair satisfying \(h(m) = h(m_0 || m_1)\) implies that \(j(E_0/\langle P_0 +~\hbox {m} Q_0\rangle ) = j(E_1/\langle P_1+m_1Q_1\rangle )\).
Firstly, the integer m is randomly selected. Then, \(m_0\) is selected as the lower n/2 bits of \(m_0\) is the same as that of m. The selection makes the first n/2 steps of the paths corresponding to m and \(m_0\) the same. Finally, we compute \(m_1\) so that the path corresponding to \(m_1\) can track the path to \(E_0/\langle P_0+mQ_0\rangle \), which is possible by deciding \(m_1\) from lower bits.
The algorithm fails when the backtracking isogeny cannot be computed at the curve \(E_1\). However, the probability of the failure is negligible by selecting the upper bits of \(m_0\) randomly. The algorithm is a probabilistic polynomial time algorithm overall, and we actually found collisions. The code to find collisions is available at the following GitHub repository: https://github.com/hedwig100/cgl-cost-evaluation.
1.2 A.2 The Cost Ratios of Each Operation in \(\mathbb {F}_p\)
The cost ratios of multiplication, square, addition, and inversion in \(\mathbb {F}_p\) are computed using Boost Multiplication Library. The computed ratios are listed in Table 3. These ratios are used to convert the complexities represented by \(\textrm{M},\textrm{S},\textrm{A}\), and \(\textrm{I}\) in Table 1 to the complexities represented only by \(\textrm{M}\) in Table 4. The acceleration ratios in Table 2 are computed from the complexities represented only by \(\textrm{M}\).
1.3 A.3 The Costs Represented only by Multiplication
The complexity represented in Table 1 is converted to the complexity represented only by \(\textrm{M}\) using the cost ratios in Table 3. The converted complexities are listed in Table 4.
Rights and permissions
Copyright information
© 2025 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Inoue, S., Aikawa, Y., Takagi, T. (2025). A Faster Variant of CGL Hash Function via Efficient Backtracking Checks. In: Mouha, N., Nikiforakis, N. (eds) Information Security. ISC 2024. Lecture Notes in Computer Science, vol 15258. Springer, Cham. https://doi.org/10.1007/978-3-031-75764-8_5
Download citation
DOI: https://doi.org/10.1007/978-3-031-75764-8_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-75763-1
Online ISBN: 978-3-031-75764-8
eBook Packages: Computer ScienceComputer Science (R0)