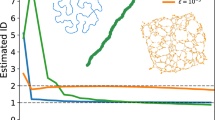
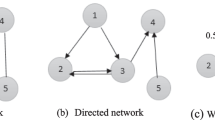
Abstract
Complex network theory has been widely demonstrated as a powerful tool in modeling and characterizing various complex systems. In the past, complex network theory has focused on the behaviors as well as the characteristics of the network nodes and edges. However, with the continuous evolution of society, traditional graph theory faces challenges due to the emergence of extermely large network structures. Recently, complex network method based statistics has attracted much attention. The new approach effectively manages very large networks and uncovers their intrinsic properties. In this paper, we present a complex network analysis model for undirected, unweighted networks based on a statistical analysis approach. This model is inspired by the ensemble model in thermostatistical physics. Based on the established mathematical model, we derive physical measures that reflect the intrinsic properties of the network, including Entropy, Free Energy, Temperature, and so on. In the experimental part, we first explored the mathematical characterization of these metrics. Then, we observed the performance of various network categories under the same metric. Finally, we applied these measures to the field of graph classification. Extensive experiments demonstrate the effectiveness and superiority of the proposed method.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Cheng, Y., Sun, F., Zhang, Y., Tao, F.: Task allocation in manufacturing: A review. J. Ind. Inf. Integr. 15, 207–218 (2019)
da Fontoura Costa, L.: Coincidence complex networks. Journal of Physics: Complexity 3(1), 015012 (mar 2022)
Statistical mechanics of complex networks: Albert, R.k., Barabá si, A.L.s. Rev. Mod. Phys. 74, 47–97 (2002)
Cimini, G., Squartini, T., Saracco, F., Garlaschelli, D., Gabrielli, A., Caldarelli, G.: The statistical physics of real-world networks. Nature Reviews Physics 1(1), 58–71 (2019)
Broido, A.D., Clauset, A.: Scale-free networks are rare. Nature communications 10(1), 1017 (2019)
Barrat, A., Weigt, M.: On the properties of small-world network models. The European Physical Journal B-Condensed Matter and Complex Systems 13, 547–560 (2000)
Amaral, L.A.N., Scala, A., Barthelemy, M., Stanley, H.E.: Classes of small-world networks. Proc. Natl. Acad. Sci. 97(21), 11149–11152 (2000)
Girvan, M., Newman, M.E.: Community structure in social and biological networks. Proc. Natl. Acad. Sci. 99(12), 7821–7826 (2002)
Newman, M.E., Girvan, M.: Finding and evaluating community structure in networks. Phys. Rev. E 69(2), 026113 (2004)
Park, J., Newman, M.E.: Statistical mechanics of networks. Phys. Rev. E 70(6), 066117 (2004)
Pathria, R.K.: Statistical mechanics. Elsevier (2016)
Wang, J., Wilson, R.C., Hancock, E.R.: Network entropy analysis using the maxwell-boltzmann partition function. In: 2016 23rd International Conference on Pattern Recognition (ICPR). pp. 1321–1326. IEEE (2016)
Zhu, H., Wu, H., Wang, J., Hancock, E.R.: Weighted network analysis using the debye model. In: Structural, Syntactic, and Statistical Pattern Recognition: Joint IAPR International Workshops, S+ SSPR 2020, Padua, Italy, January 21–22, 2021, Proceedings. pp. 153–163. Springer (2021)
Kipf, T.N., Welling, M.: Semi-supervised classification with graph convolutional networks. In: International Conference on Learning Representations (2017)
Watts, D.J., Strogatz, S.H.: Collective dynamics of ‘small-world’ networks. nature 393(6684), 440–442 (1998)
On the evolution of random graphs: Erd6s, P., Rényi, A. Publ. Math. Inst. Hungar. Acad. Sci 5, 17–61 (1960)
Newman, M.E., Watts, D.J.: Renormalization group analysis of the small-world network model. Phys. Lett. A 263(4–6), 341–346 (1999)
Kaviani, S., Sohn, I.: Application of complex systems topologies in artificial neural networks optimization: An overview. Expert Syst. Appl. 180, 115073 (2021)
Brede, M.: Networks-an introduction. mark ej newman.(2010, oxford university press.) isbn-978-0-19-920665-0. (2012)
Kunegis, J.: Konect: the koblenz network collection. In: Proceedings of the 22nd International Conference on World Wide Web. pp. 1343–1350. WWW ’13 Companion, Association for Computing Machinery, New York, NY, USA (2013)
Rossi, R.A., Ahmed, N.K.: The network data repository with interactive graph analytics and visualization. In: AAAI (2015)
Newman, M.E.J.: The structure and function of complex networks. SIAM Rev. 45(2), 167–256 (2003)
Zhang, M., Cui, Z., Neumann, M., Chen, Y.: An end-to-end deep learning architecture for graph classification. In: Proceedings of the AAAI conference on artificial intelligence. vol. 32 (2018)
Arnaiz-Rodríguez, A., Begga, A., Escolano, F., Oliver, N.M.: Diffwire: Inductive graph rewiring via the lovász bound. In: Learning on Graphs Conference. pp. 15–1. PMLR (2022)
Bacciu, D., Di Sotto, L.: A non-negative factorization approach to node pooling in graph convolutional neural networks. In: AI IA 2019–Advances in Artificial Intelligence. pp. 294–306. Springer (2019)
Acknowledgements
This work is supported by the Natural Science Foundation of Jiangsu Higher Educational Institution of China(Grant No.24KJB510049), and Research Development Fund (RDF-23-01-044) at Xi’an Jiaotong-Liverpool University.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2025 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Zhao, X., Wu, X., Wang, J. (2025). Explore Statistical Properties of Undirected Unweighted Networks from Ensemble Models. In: Antonacopoulos, A., Chaudhuri, S., Chellappa, R., Liu, CL., Bhattacharya, S., Pal, U. (eds) Pattern Recognition. ICPR 2024. Lecture Notes in Computer Science, vol 15327. Springer, Cham. https://doi.org/10.1007/978-3-031-78398-2_9
Download citation
DOI: https://doi.org/10.1007/978-3-031-78398-2_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-78397-5
Online ISBN: 978-3-031-78398-2
eBook Packages: Computer ScienceComputer Science (R0)