Abstract
In the absence of any observation system or low veracity of the data, it is possible to provide control over a limited time interval basing on a high-precision control object model used.
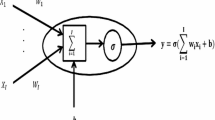
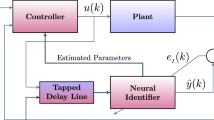
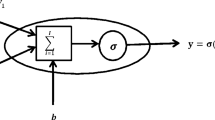
The paper proposes to use a multilayer artificial neural network (ANN) to obtain such a model. In this case, instead of the ordinary differential equation (ODE) system in the Cauchy form, we get a mixed ODE-ANN mathematical model, the parameters of which are tuned to the dynamics of a particular control object. The paper describes the process of identification of the control object model including obtaining a sufficient volume of the training sample. General data properties are formulated to obtain a good model from the point of view of use in control problems.
The problem of optimal control for an object described with ANN-based model is formulated and numerical approach for its solution is proposed. An example of solving the optimal control problem for a mobile robot based on the identified neural network model is given.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Tachinina, O.M., Lysenko, O.I., Alekseeva, I.V., Tureichuk, A.M.: Algorithm of stabilization of uav on a given trajectory of motion with allowance for possible retargeting. In: 2018 IEEE 5th International Conference on Methods and Systems of Navigation and Motion Control (MSNMC), Kiev, Ukraine, pp. 132–134 (2018). https://doi.org/10.1109/MSNMC.2018.8576272
Ning, Y., Yue, M., Ding, L., Gao, H.: Time-optimal point stabilization control for WIP vehicles using quasi-convex optimization and B-spline adaptive interpolation techniques. IEEE Trans. Syst. Man Cybern. Syst. 51(5), 3293–3303 (2021). https://doi.org/10.1109/TSMC.2019.2920958
Young, L.C.: Lectures on the Calculus of Variations and Optimal Control Theory, 2nd edn. Chelsea Pub. Co., New York (1980)
Pontryagin, L.S., Boltyanskii, V.G., Gamkreidze, R.V., Mishchenko, E.F.: The Mathematical Theory of Optimal Processes. Division of John Wiley and Sons Inc, New York (1962)
De León, C.L.C.-D., et al.: Parameter identification of a robot arm manipulator based on a convolutional neural network. IEEE Access 10, 55002–55019 (2022). https://doi.org/10.1109/ACCESS.2022.3177209
Liu, G.P.: Nonlinear Identification and Control: A Neural Network Approach. Springer, Heidelberg (2012). https://doi.org/10.1007/978-1-4471-0345-5
Williams, G., Drews, P., Goldfain, B., Rehg, J.M., Theodorou, E.A.: Aggressive driving with model predictive path integral control. In: Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA)), Stockholm, Sweden, pp. 1433–1440 (2016)
Shmalko, E., Rumyantsev, Y., Baynazarov, R., Yamshanov, K.: Identification of neural network model of robot to solve the optimal control problem. Inform. Autom. 20, 1254–1278 (2021). https://doi.org/10.15622/ia.20.6.3
Diveev, A.I., Konstantinov, S.V.: Study of the practical convergence of evolutionary algorithms for the optimal program control of a wheeled robot. J. Comput. Syst. Sci. Int. 57(4), 561–580 (2018). https://doi.org/10.1134/S106423071804007X
Karpenko, A.P., Seliverstov, E.Yu.: Global optimization by the particle swarm method. Rev. Inform. Tekhnol. 2, 25–34 (2010)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2025 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Shmalko, E., Prokopiev, I., Diveev, A., Yamshanov, K. (2025). Improving Feasibility of Optimal Control via Obtaining High-Precision Model. In: Sergeyev, Y.D., Kvasov, D.E., Astorino, A. (eds) Numerical Computations: Theory and Algorithms. NUMTA 2023. Lecture Notes in Computer Science, vol 14476. Springer, Cham. https://doi.org/10.1007/978-3-031-81241-5_33
Download citation
DOI: https://doi.org/10.1007/978-3-031-81241-5_33
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-81240-8
Online ISBN: 978-3-031-81241-5
eBook Packages: Computer ScienceComputer Science (R0)