Skip to main content
Springer Nature Link
Log in

Well-posedness of Networked Hyperbolic Systems of Balance Laws

  • Chapter
  • First Online:
Constrained Optimization and Optimal Control for Partial Differential Equations

Part of the book series: International Series of Numerical Mathematics ((ISNM,volume 160))

Abstract

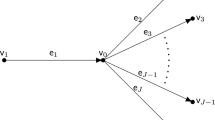
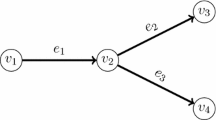
We present an overview on recent results concerning hyperbolic systems on networks. We present a summary of theoretical results on existence, uniqueness and stability. The established theory extends previously known results on the Cauchy problem for nonlinear, 2×2 hyperbolic balance laws. The proofs are based on Wave-Front Tracking and therefore we present detailed results on the Riemann problem first.

Mathematics Subject Classification (2000). 35L65, 49J20.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. D. Amadori. Initial-boundary value problems for nonlinear systems of conservation laws. NoDEA Nonlinear Differential Equations Appl., 4(1):1–42, 1997.

    MathSciNet  MATH  Google Scholar 

  2. D. Amadori and R.M. Colombo. Continuous dependence for 2×2 conservation laws with boundary. J. Differential Equations, 138(2):229–266, 1997.

    MathSciNet  MATH  Google Scholar 

  3. D. Amadori and G. Guerra. Uniqueness and continuous dependence for systems of balance laws with dissipation. Nonlinear Anal., 49(7, Ser. A: Theory Methods):987–1014, 2002.

    MathSciNet  MATH  Google Scholar 

  4. F. Ancona and G.M. Coclite. On the attainable set for Temple class systems with boundary controls. SIAM J. Control Optim., 43(6):2166–2190 (electronic), 2005.

    MathSciNet  MATH  Google Scholar 

  5. F. Ancona and A. Marson. On the attainable set for scalar nonlinear conservation laws with boundary control. SIAM J. Control Optim., 36:290–312, 1998.

    MathSciNet  MATH  Google Scholar 

  6. F. Ancona and A. Marson. Asymptotic stabilization of systems of conservation laws by controls acting at a single boundary point. Control Methods in PDE-Dynamical Systems (Amer. Math. Soc. Providence), 426, 2007.

    Google Scholar 

  7. D. Armbruster, P. Degond, and C. Ringhofer. A model for the dynamics of large queuing networks and supply chains. SIAM J. Appl. Math., 66:896–920, 2006.

    MathSciNet  MATH  Google Scholar 

  8. A. Aw and M. Rascle. Resurrection of second-order models of traffic flow? SIAM J. Appl. Math., 60:916–944, 2000.

    MathSciNet  MATH  Google Scholar 

  9. M.K. Banda, M. Herty, and A. Klar. Coupling conditions for gas networks governed by the isothermal Euler equations. Networks and Heterogeneous Media, 1(2):275–294, 2006.

    MathSciNet  MATH  Google Scholar 

  10. M.K. Banda, M. Herty, and A. Klar. Gas flow in pipeline networks. Networks and Heterogeneous Media, 1(1):41–56, 2006.

    MathSciNet  MATH  Google Scholar 

  11. S. Bolch, G. Greiner, H. de Meer, and K. Trivedi. Queuing Networks and Markov Chains. John Wiley & Sons, New York, 1998.

    MATH  Google Scholar 

  12. A. Bressan. Hyperbolic systems of conservation laws: The one-dimensional Cauchy problem, volume 20 of Oxford Lecture Series in Mathematics and its Applications. Oxford University Press, Oxford, 2000.

    Google Scholar 

  13. A. Bressan and G.M. Coclite. On the boundary control of systems of conservation laws. SIAM J. Control Optim., 41:607–622, 2002.

    MathSciNet  MATH  Google Scholar 

  14. A. Bressan and A. Marson. A maximum principle for optimally controlled systems of conservation laws. Rend. Sem. Mat. Univ. Padova, 94:79–94, 1995.

    MathSciNet  MATH  Google Scholar 

  15. I. Cameron. Using an excel-based model for steady-state and transient simulation. Technical report, TransCanada Transmission Company, 2000.s

    Google Scholar 

  16. C. Castro, F. Palacios, and E. Zuazua. An alternating descent method for the optimal control of the inviscid Burgers equation in the presence of shocks. Math. Models Methods Appl. Sci., 18:369–416, 2008.

    MathSciNet  MATH  Google Scholar 

  17. K.S. Chapman and M. Abbaspour. Non-isothermal Compressor Station Transient Modeling. Technical report, PSIG, 2003.

    Google Scholar 

  18. N.H. Chen. An explicit equation for friction factor in pipe. Ind. Eng. Chem. Fund., 18(3):296–297, 1979.

    Google Scholar 

  19. G. Coclite, M. Garavello, and B. Piccoli. Traffic flow on a road network. SIAM J. Math. Anal., 36(6):1862–1886, 2005.

    MathSciNet  MATH  Google Scholar 

  20. R. Colombo and A. Groli. Minimising stop and go waves to optimise traffic flow. Appl. Math. Lett., 17(6):697–701, 2004.

    MathSciNet  MATH  Google Scholar 

  21. R.M. Colombo and M. Garavello. A well-posed Riemann problem for the p-system at a junction. Networks and Heterogeneous Media, 1:495–511, 2006.

    MathSciNet  MATH  Google Scholar 

  22. R.M. Colombo and M. Garavello. On the Cauchy problem for the 𝑝-system at a junction. SIAM J. Math. Anal., 39:1456–1471, 2008.

    MathSciNet  MATH  Google Scholar 

  23. R.M. Colombo and G. Guerra. Differential equations in metric spaces with applications. Discrete and Continuous Dynamical Systems, 2007. To appear. Preprint http://arxiv.org/abs/0712.0560.

  24. R.M. Colombo and G. Guerra. Hyperbolic balance laws with a non local source. Communications in Partial Differential Equations, 32(12), 2007.

    Google Scholar 

  25. R.M. Colombo and G. Guerra. On general balance laws with boundary. Preprint, 2008.

    Google Scholar 

  26. R.M. Colombo, G. Guerra, M. Herty, and V. Schleper. Optimal control in networks of pipes and canals. SIAM Journal on Control and Optimization, 48(3):2032–2050, 2009.

    MathSciNet  MATH  Google Scholar 

  27. R.M. Colombo, M. Herty, and V. Sachers. On 2×2 conservation laws at a junction. SIAM J. Math. Anal., 40(2):605–622, 2008.

    MathSciNet  MATH  Google Scholar 

  28. R.M. Colombo and F. Marcellini. Smooth and discontinuous junctions in the psystem. to appear in J. Math. Anal. Appl., 2009.

    Google Scholar 

  29. G. Crasta and B. Piccoli. Viscosity solutions and uniqueness for systems of inhomogeneous balance laws. Discrete Contin. Dyn. Syst., 3(4):477–502, 1997.

    MathSciNet  MATH  Google Scholar 

  30. C.M. Dafermos. Hyperbolic Conservation Laws in Continuum Physics, volume 325 of A Series of Comprehensive Studies in Mathematics. Springer Verlag, Berlin, Heidelberg, New York, 2005. Second edition.

    Google Scholar 

  31. C. D’Apice and R. Manzo. Calculation of predicted average packet delay and its application for flow control in data network. J. Inf. Optimization Sci., 27:411–423, 2006.

    MATH  Google Scholar 

  32. C. D’Apice, R. Manzo, and B. Piccoli. Packet flow on telecommunication networks. SIAM J. Math. Anal., 38(3):717–740, 2006.

    MathSciNet  MATH  Google Scholar 

  33. J. de Halleux, C. Prieur, J.-M. Coron, B. d’Andréa Novel, and G. Bastin. Boundary feedback control in networks of open channels. Automatica J. IFAC, 39(8):1365–1376, 2003.

    MathSciNet  MATH  Google Scholar 

  34. J. de Halleux, C. Prieur, J.-M. Coron, B. d’Andréa Novel, and G. Bastin. Boundary feedback control in networks of open channels. Automatica J. IFAC, 39(8):1365–1376, 2003.

    MathSciNet  MATH  Google Scholar 

  35. R.J. DiPerna. Global existence of solutions to nonlinear hyperbolic systems of conservation laws. J. Differ. Equations, 20:187–212, 1976.

    MathSciNet  MATH  Google Scholar 

  36. C. Donadello and A. Marson. Stability of front tracking solutions to the initial and boundary value problem for systems of conservation laws. NoDEA Nonlinear Differential Equations Appl., 14(5-6):569–592, 2007.

    MathSciNet  MATH  Google Scholar 

  37. K. Ehrhardt and M. Steinbach. Nonlinear gas optimization in gas networks. In H. Bock, E. Kostina, H. Pu, and R. Rannacher, editors, Modeling, Simulation and Optimization of Complex Processes. Springer Verlag, Heidelberg, 2005.

    MATH  Google Scholar 

  38. I.R. Ellul, G. Saether, and M.E. Shippen. The modeling of multiphase systems under steady-state and transient conditions a tutorial. Technical report, PSIG, 2004.

    Google Scholar 

  39. M. Garavello and B. Piccoli. Traffic flow on a road network using the aw-rascle model. Commun. Partial Differ. Equations, 31(1-3):243–275, 2006.

    MathSciNet  MATH  Google Scholar 

  40. O. Glass. On the controllability of the 1-D isentropic Euler equation. J. Eur. Math. Soc. (JEMS), 9(3):427–486, 2007.

    MathSciNet  MATH  Google Scholar 

  41. J. Goodman. Initial Boundary Value Problems for Hyperbolic Systems of Conservation Laws. PhD thesis, California University, 1982.

    Google Scholar 

  42. S. Göttlich, M. Herty, and A. Klar. Modelling and optimization of supply chains on complex networks. Communications in Mathematical Sciences, 4(2):315–330, 2006.

    MathSciNet  MATH  Google Scholar 

  43. G. Guerra, F. Marcellini, and V. Schleper. Balance laws with integrable unbounded sources. SIAM Journal of Mathematical Analysis, 41(3), 2009.

    Google Scholar 

  44. M. Gugat. Nodal control of conservation laws on networks. Sensitivity calculations for the control of systems of conservation laws with source terms on networks. Cagnol, John (ed.) et al., Control and boundary analysis. Selected papers based on the presentation at the 21st conference on system modeling and optimization, Sophia Antipolis, France, July 21–25, 2003. Boca Raton, FL: Chapman & Hall/CRC. Lecture Notes in Pure and Applied Mathematics 240, 201–215 (2005), 2005.

    Google Scholar 

  45. M. Gugat and G. Leugering. Global boundary controllability of the de St. Venant equations between steady states. Annales de l’Institut Henri Poincaré, Nonlinear Analysis, 20(1):1–11, 2003.

    MathSciNet  MATH  Google Scholar 

  46. M. Gugat and G. Leugering. Global boundary controllability of the saint-venant system for sloped canals with friction. Annales de l’Institut Henri Poincaré, Nonlinear Analysis, 26(1):257–270, 2009.

    MathSciNet  MATH  Google Scholar 

  47. M. Gugat, G. Leugering, and E.J.P. Georg Schmidt. Global controllability between steady supercritical flows in channel networks. Math. Methods Appl. Sci., 27(7):781–802, 2004.

    MathSciNet  MATH  Google Scholar 

  48. M. Gugat, G. Leugering, K. Schittkowski, and E.J.P.G. Schmidt. Modelling, stabilization, and control of flow in networks of open channels. In Online optimization of large scale systems, pages 251–270. Springer, Berlin, 2001.

    MATH  Google Scholar 

  49. M. Herty. Modeling, simulation and optimization of gas networks with compressors. Networks and Heterogenous Media, 2:81, 2007.

    MathSciNet  MATH  Google Scholar 

  50. M. Herty and M. Rascle. Coupling conditions for a class of second-order models for traffic flow. SIAM Journal on Mathematical Analysis, 38, 2006.

    Google Scholar 

  51. H. Holden and N.H. Risebro. Riemann problems with a kink. SIAM J. Math. Anal., 30:497–515, 1999.

    MathSciNet  MATH  Google Scholar 

  52. C. Kelling, K. Reith, and E. Sekirnjak. A Practical Approach to Transient Optimization for Gas Networks. Technical report, PSIG, 2000.

    Google Scholar 

  53. J. Králink, P. Stiegler, Z. Vostrý, and J. Závorka. Modelle für die Dynamik von Rohrleitungsnetzen – theoretischer Hintergrund. Gas-Wasser-Abwasser, 64(4):187–193, 1984.

    Google Scholar 

  54. C.D. Laird, L.T. Biegler, B.G. van BloemenWaanders, and R.A. Barlett. Contamination source determination for water networks. A.S.C.E. Journal of Water Resources Planning and Management, 131(2):125–134, 2005.

    Google Scholar 

  55. P.D. Lax. Hyperbolic systems of conservation laws. {II}. Comm. Pure Appl. Math., 10:537–566, 1957.

    MATH  Google Scholar 

  56. G. Leugering and E.J.P.G. Schmidt. On the modeling and stabilization of flows in networks of open canals. SIAM J. Control Opt., 41(1):164–180, 2002.

    MATH  Google Scholar 

  57. R.J. LeVeque. Numerical Methods for Conservation Laws. Lectures in Mathematics ETH Zürich. Birkhäuser Verlag, 2006. Third edition.

    Google Scholar 

  58. T.-T. Li. Exact controllability for quasilinear hyperbolic systems and its application to unsteady flows in a network of open canals. Mathematical Methods in the Applied Sciences, 27:1089–1114, 2004.

    MathSciNet  MATH  Google Scholar 

  59. T.-T. Li and B.-P. Rao. Exact boundary controllability for quasi-linear hyperbolic systems. SIAM J. Control Optim., 41(6):1748–1755, 2003.

    MathSciNet  MATH  Google Scholar 

  60. T.-T. Li and B.-P. Rao. Exact boundary controllability of unsteady flows in a treelike network of open canals. Methods Appl. Anal., 11(3):353–365, 2004.

    MathSciNet  MATH  Google Scholar 

  61. M.J. Lighthill and G.B. Whitham. On kinematic waves. Proc. Royal Soc. Edinburgh, 229:281–316, 1955.

    MATH  Google Scholar 

  62. A. Martin, M. Möller, and S. Moritz. Mixed integer models for the stationary case of gas network optimization. Math. Programming.

    Google Scholar 

  63. A. Osiadacz. Optimization of high pressure gas networks using hierarchical systems theory. Technical report, Warsaw University, 2002.

    Google Scholar 

  64. A.J. Osiadacz. Simulation and analysis of gas networks. Gulf Publishing Company, Houston, 1989.

    MATH  Google Scholar 

  65. A.J. Osiadacz. Different transient models – limitations, advantages and disadvantages. Technical report, PSIG, 1996.

    Google Scholar 

  66. Pipeline Simulation Interest Group. www.psig.org.

  67. M. Steinbach. On PDE solution in transient optimization of gas networks. J. Comput. Appl. Math., 203(2):345–361, 2007.

    MathSciNet  MATH  Google Scholar 

  68. S. Ulbrich. Adjoint-based derivative computations for the optimal control of discontinuous solutions of hyperbolic conservation laws. Syst. Control Lett,, 48(3–4):313–328, 2003.

    MathSciNet  MATH  Google Scholar 

  69. J. Zhou and M.A. Adewumi. Simulation of transients in natural gas pipelines using hybrid tvd schemes. Int. J. Numer. Meth. Fluids, 32:407–437, 2000.

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Erlangen–Nürnberg, D-91058, Erlangen, Germany

    Martin Gugat & Günther Leugering

  2. Department of Mathematics, RWTH Aachen University, D-52056, Aachen, Germany

    Michael Herty

  3. Department of Mathematics, TU Kaiserslautern, D-67663, Kaiserslautern, Germany

    Axel Klar

  4. Department of Mathematics, University of Stuttgart, D-70569, Stuttgart, Germany

    Veronika Schleper

Authors
  1. Martin Gugat
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael Herty
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Axel Klar
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Günther Leugering
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Veronika Schleper
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Martin Gugat .

Editor information

Editors and Affiliations

  1. , Department Mathematik, Universität Erlangen-Nürnberg, Martensstr. 3, Erlangen, 91058, Germany

    Günter Leugering

  2. , Fakultät Bio- und Chemieingenieurwesen, Technische Universität Dortmund, Geschossbau 2, Dortmund, 44221, Germany

    Sebastian Engell

  3. , Institut für Mathematik, Humboldt-Universität zu Berlin, Rudower Chaussee 25, Berlin, 12489, Germany

    Andreas Griewank

  4. , Fachbereich Mathematik, Universität Hamburg, Bundesstr. 55, Hamburg, 20146, Germany

    Michael Hinze

  5. , Institut für Angewandte Mathematik, Ruprecht-Karls-Universität Heidelberg, Im Neuenheimer Feld 293, Heidelberg, 69120, Germany

    Rolf Rannacher

  6. , FB 4 - Department Mathematik, Universität Trier, Trier, 54286, Germany

    Volker Schulz

  7. Fakultät für Mathematik, M1, Lehrstuhl für Mathematische Optimierung, Technische Universität München, Boltzmannstr. 3, Garching bei München, 85748, Germany

    Michael Ulbrich

  8. , Fachbereich Mathematik, Technische Universität Darmstadt, Dolivostrasse 15, Darmstadt, 64293, Germany

    Stefan Ulbrich

Rights and permissions

Reprints and permissions

Copyright information

© 2012 Springer Basel AG

About this chapter

Cite this chapter

Gugat, M., Herty, M., Klar, A., Leugering, G., Schleper, V. (2012). Well-posedness of Networked Hyperbolic Systems of Balance Laws. In: Leugering, G., et al. Constrained Optimization and Optimal Control for Partial Differential Equations. International Series of Numerical Mathematics, vol 160. Birkhäuser, Basel. https://doi.org/10.1007/978-3-0348-0133-1_7

Download citation

Publish with us

Policies and ethics