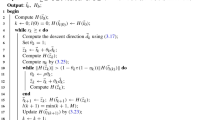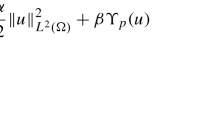Skip to main content
Springer Nature Link
Log in

A Globalized Semi-smooth Newton Method for Variational Discretization of Control Constrained Elliptic Optimal Control Problems

  • Chapter
  • First Online:
Constrained Optimization and Optimal Control for Partial Differential Equations

Part of the book series: International Series of Numerical Mathematics ((ISNM,volume 160))

Abstract

When combining the numerical concept of variational discretization introduced in [Hin03, Hin05] and semi-smooth Newton methods for the numerical solution of pde constrained optimization with control constraints [HIK03, Ulb03] special emphasis has to be placed on the implementation, convergence and globalization of the numerical algorithm. In the present work we address all these issues following [HV]. In particular we prove fast local convergence of the algorithm and propose a globalization strategy which is applicable in many practically relevant mathematical settings. We illustrate our analytical and algorithmical findings by numerical experiments.

Mathematics Subject Classification (2000). 49J20, 49K20, 49M15.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. Klaus Deckelnick and Michael Hinze. Convergence of a finite element approximation to a state-constrained elliptic control problem. SIAM J. Numer. Anal., 45(5):1937–1953, 2007.

    Article  MathSciNet  MATH  Google Scholar 

  2. Klaus Deckelnick and Michael Hinze. A finite element approximation to elliptic control problems in the presence of control and state constraints. Preprint, Hamburger Beitr. z. Ang. Math. 2007–01, 2007.

    Google Scholar 

  3. M. Hintermüller, K. Ito, and K. Kunisch. The primal-dual active set strategy as a semismooth Newton method. SIAM J. Optim., 13(3):865–888, 2003.

    Article  MathSciNet  MATH  Google Scholar 

  4. Michael Hinze. A generalized discretization concept for optimal control problems with control constraints. Technical Report Preprint MATH-NM-02-2003, Institut für Numerische Mathematik, Technische Universität Dresden, 2003.

    Google Scholar 

  5. Michael Hinze. A variational discretization concept in control constrained optimization: The linear-quadratic case. Comput. Optim. Appl., 30(1):45–61, 2005.

    Article  MathSciNet  MATH  Google Scholar 

  6. Michael Hinze and Christian Meyer. Numerical analysis of Lavrentievregularized state-constrained elliptic control problems. Comp. Optim. Appl., 2008.

    Google Scholar 

  7. M. Hinze, R. Pinnau, M. Ulbrich, and S. Ulbrich. Optimization with PDE constraints. Mathematical Modelling: Theory and Applications 23. Dordrecht: Springer., 2009.

    Google Scholar 

  8. Michael Hintermüller and Michael Ulbrich. A mesh-independence result for semismooth Newton methods. Mathematical Programming, 101:151–184, 2004.

    Article  MathSciNet  MATH  Google Scholar 

  9. Michael Hinze and Morten Vierling. A globalized semi-smooth Newton method for variational discretization of control constrained elliptic optimal control problems. In Constrained Optimization and Optimal Control for Partial Differential Equations. Birkhäuser, 2011, to appear.

    Google Scholar 

  10. Klaus Krumbiegel and Arnd Rösch. A new stopping criterion for iterative solvers for control constrained optimal control problems. Archives of Control Sciences, 18(1):17–42, 2008.

    MathSciNet  MATH  Google Scholar 

  11. Michael Ulbrich. Semismooth Newton methods for operator equations in function spaces. SIAM J. Optim., 13(3):805–841, 2003.

    Article  MathSciNet  MATH  Google Scholar 

  12. Michael Ulbrich. A new mesh-independence result for semismooth Newton methods. Oberwolfach Rep., 4:78–81, 2009.

    Google Scholar 

  13. Morten Vierling. Ein semiglattes Newtonverfahren für semidiskretisierte steuerungsbeschränkte Optimalsteuerungsprobleme. Master’s thesis, Universität Hamburg, 2007.

    Google Scholar 

  14. Stefan Volkwein and Fredi Tröltzsch. Pod a posteriori error estimates for linear-quadratic optimal control problems. Computational Optimization and Applications, 44(1):83–115, 2009.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Schwerpunkt Optimierung und Approximation, Universität Hamburg, Bundesstraße 55, D-20146, Hamburg, Germany

    Michael Hinze & Morten Vierling

Authors
  1. Michael Hinze
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Morten Vierling
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Michael Hinze .

Editor information

Editors and Affiliations

  1. , Department Mathematik, Universität Erlangen-Nürnberg, Martensstr. 3, Erlangen, 91058, Germany

    Günter Leugering

  2. , Fakultät Bio- und Chemieingenieurwesen, Technische Universität Dortmund, Geschossbau 2, Dortmund, 44221, Germany

    Sebastian Engell

  3. , Institut für Mathematik, Humboldt-Universität zu Berlin, Rudower Chaussee 25, Berlin, 12489, Germany

    Andreas Griewank

  4. , Fachbereich Mathematik, Universität Hamburg, Bundesstr. 55, Hamburg, 20146, Germany

    Michael Hinze

  5. , Institut für Angewandte Mathematik, Ruprecht-Karls-Universität Heidelberg, Im Neuenheimer Feld 293, Heidelberg, 69120, Germany

    Rolf Rannacher

  6. , FB 4 - Department Mathematik, Universität Trier, Trier, 54286, Germany

    Volker Schulz

  7. Fakultät für Mathematik, M1, Lehrstuhl für Mathematische Optimierung, Technische Universität München, Boltzmannstr. 3, Garching bei München, 85748, Germany

    Michael Ulbrich

  8. , Fachbereich Mathematik, Technische Universität Darmstadt, Dolivostrasse 15, Darmstadt, 64293, Germany

    Stefan Ulbrich

Rights and permissions

Reprints and permissions

Copyright information

© 2012 Springer Basel AG

About this chapter

Cite this chapter

Hinze, M., Vierling, M. (2012). A Globalized Semi-smooth Newton Method for Variational Discretization of Control Constrained Elliptic Optimal Control Problems. In: Leugering, G., et al. Constrained Optimization and Optimal Control for Partial Differential Equations. International Series of Numerical Mathematics, vol 160. Birkhäuser, Basel. https://doi.org/10.1007/978-3-0348-0133-1_9

Download citation

Publish with us

Policies and ethics