Abstract
We fit a Hidden Markov Model (HMM) to patient arrivals data, represented as a discrete data trace. The processing of the data trace makes use of a simple binning technique, followed by clustering, before it is input into the Baum-Welch algorithm, which estimates the parameters of the underlying Markov chain’s state-transition matrix. Upon convergence, the HMM predicts its own synthetic traces of patient arrivals, behaving as a fluid input model. The Viterbi algorithm then decodes the hidden states of the HMM, further explaining the varying rate of patient arrivals at different times of the hospital schedule. The HMM is validated by comparing means, standard deviations and autocorrelation functions of raw and synthetic traces. Finally, we explore an efficient optimal parameter initialization for the HMM, including choosing the number of hidden states. We summarize our findings, comparing results with other work in the field, and proposals for future work.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
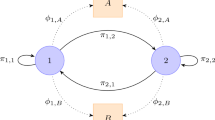
\(A\) is the state transition matrix, \(B\) is the observation emissions matrix, and \(\pi \) is the initial distribution.
References
Harrison PG, Harrison SK, Patel NM, Zertal S (2012) Storage workload modelling by hidden markov models: application to flash memory. Perform Eval 69:17–40
Baum LE, Petrie T (1966) Stastical inference for probabilistic functions of finite markov chains. Ann Math Stat 37:1554–1563
Baum LE, Eagon JA (1967) An inequality with applications to statistical estimation for probabilistic functions of a markov process and to a model for ecology. Bull Am Math Soc 73:360–363
Rabiner LR (1989) A tutorial on hidden markov models and selected applications in speech recognition. IEEE 77:257–286
Ashraf J, Iqbal N, Khattak NS, Zaidi, AM (2010) Speaker Independent Urdu Speech Recognition Using HMM
Burge C, Karlin S (1997) Prediction of complete gene structures in human genomic DNA. J Mol Biol. Stanford University, California, USA, Computer and Information Sciences, pp 78–94
Baum LE, Petrie T, Soules G, Weiss N (1970) A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains. Ann Math Stat 41:164–171
Viterbi AJ (1967) Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Trans Inf Theor 13:260–269
Chis T (2011) Hidden markov models: applications to flash memory data and hospital arrival times. Department of Computing, Imperial College London
Rabiner LR, Juang BH (1986) An introduction to hidden markov models. IEEE ASSP Mag 3:4–16
Au-Yeung SWM, Harder U, McCoy E, Knottenbelt WJ (2009) Predicting patient arrivals to an accident and emergency department. Emerg Med J 26:241–244
Zhang L, Chan KP (2010) Bigram HMM with context distribution clustering for unsupervised Chinese part-of-speech tagging. Department of Computer Science, Hong Kong
Brand M (1999) An entropic estimator for structure discovery. In; Proceedings of the (1998) conference on advances in neural information processing systems II. MIT Press. MA, USA, Cambridge, pp 723–29
Krough A, Brown M, Mian S, Sjolander K, Haussler D (1994) Hidden markov models in computational biology. J Mo Biol 235:1501–1531 (University of California, Santa Cruz, USA, Computer and Information Sciences)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer International Publishing Switzerland
About this paper
Cite this paper
Chis, T., Harrison, P.G. (2013). Analysing and Predicting Patient Arrival Times. In: Gelenbe, E., Lent, R. (eds) Information Sciences and Systems 2013. Lecture Notes in Electrical Engineering, vol 264. Springer, Cham. https://doi.org/10.1007/978-3-319-01604-7_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-01604-7_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-01603-0
Online ISBN: 978-3-319-01604-7
eBook Packages: Computer ScienceComputer Science (R0)