Abstract
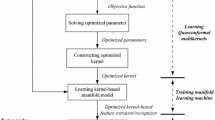
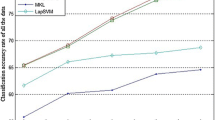
This paper presents a framework that optimizes kernel-based manifold embedding for the characterization of multispectral image data. The hypothesis is that data manifolds corresponding to high-dimensional images can have varying characteristics and types of nonlinearity. As a result, kernel functions must be selected from a wide range of transformations and tuned on an image- and patient-basis. To this end, we introduce a new measure to assess the quality of the kernel transformations that takes into account both local and global relationships in nonlinear manifolds. Furthermore, the calculated measures for each kernel are used to combine the different kernel transformations further highlight the tissue constituents in all regions of the image. Validation with phantom and real multispectral image data shows improvement in the visualization and characterization of the tissue constituents.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Chen, L., Buja, A.: Local multidimensional scaling for nonlinear dimension reduction, graph drawing and proximity analysis. Journal of the American Statistical Association 104(485), 209–219 (2009)
Hofmann, T., Schölkopf, B., Smola, A.J.: Kernel Methods in Machine Learning. The Annals of Statistics 36(3), 1171–1220 (2008)
Hordley, S., Finalyson, G., Morovic, P.: A Multispectral Image Database and its Application to Image Rendering Across Illumination. In: Proc. 3rd Int. Conf. on Image and Graphics (ICIG), Hong-Kong, China, pp. 394–397 (2004), http://www2.cmp.uea.ac.uk/Research/compvis/MultiSpectralDB.htm
Kouropteva, O., Okun, O., Pietkäinen, M.: Incremental locally linear embedding. Pattern Recognition 38(10), 1764–1767 (2005)
Lee, J.A., Verleysen, M.: Quality assessment of dimensionality reduction: Rank-based criteria. Neurocomputing 72(7-9), 1431–1443 (2009)
Maaten, L.V.D., Postma, E., Herik, H.V.D.: Dimensionality reduction: a comparative review. Tech. Rep. TiCC-TR 2009-05, Tilburg University, Tilburg, The Netherlands (2009)
Menze, B., Jakab, A., Bauer, S., Reyes, M., Prastawa, M., van Leemput, K.: Challenge on Multimodal Brain Tumor Segmentation (MICCAI-BRATS). In: Proc. MICCAI 2012 (2012), http://www2.imm.dtu.dk/projects/BRATS2012
Tanabe, H., Ho, T.B., Nguyen, C.H., Kawasaki, S.: Simple but effective methods for combining kernels in computational biology. In: IEEE Int. Conf. on Research, Innovation and Vision for the Future (RIVF), pp. 71–78 (2008)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer International Publishing Switzerland
About this paper
Cite this paper
Zimmer, V.A.M., Fonolla, R., Lekadir, K., Piella, G., Hoogendoorn, C., Frangi, A.F. (2013). Patient-Specific Manifold Embedding of Multispectral Images Using Kernel Combinations. In: Wu, G., Zhang, D., Shen, D., Yan, P., Suzuki, K., Wang, F. (eds) Machine Learning in Medical Imaging. MLMI 2013. Lecture Notes in Computer Science, vol 8184. Springer, Cham. https://doi.org/10.1007/978-3-319-02267-3_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-02267-3_11
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-02266-6
Online ISBN: 978-3-319-02267-3
eBook Packages: Computer ScienceComputer Science (R0)