Abstract
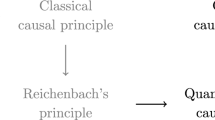
In the paper it will be argued that embracing noncommuting common causes in the causal explanation of quantum correlations in algebraic quantum field theory has the following two beneficial consequences: it helps (i) to maintain the validity of Reichenbach’s Common Causal Principle and (ii) to provide a local common causal explanation for a set of correlations violating the Bell inequality.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Butterfield, J. 1989. A spacetime approach to the bell inequality. In Philosophical consequences of quantum theory, ed. J. Cushing and E. McMullin, 114–144. Notre Dame: University of Notre Dame Press.
Butterfield, J. 1995. Vacuum correlations and outcome independence in algebraic quantum field theory. In Fundamental problems in quantum theory, annals of the New York Academy of Sciences, proceedings of a conference in honour of John Wheeler, ed. D. Greenberger and A. Zeilinger, 768–785.
Butterfield, J. 2007. Stochastic Einstein locality revisited. The British Journal for the Philosophy of Science 58: 805–867.
Haag, R. 1992. Local quantum physics. Berlin: Springer.
Halvorson, H. 2007. Algebraic quantum field theory. In Philosophy of physics, ed. J. Butterfield and J. Earman, vol. I, 731–922. Amsterdam: Elsevier.
Halvorson, H., and R. Clifton. 2000. Generic bell correlation between arbitrary local algebras in quantum field theory. Journal of Mathematical Physics 41: 1711–1717.
Hofer-Szabó, G., and P. Vecsernyés. 2012a. Reichenbach’s common cause principle in algebraic quantum field theory with locally finite degrees of freedom. Foundations of Physics 42: 241–255.
Hofer-Szabó, G., and P. Vecsernyés. 2012b. Noncommuting local common causes for correlations violating the Clauser–Horne inequality. Journal of Mathematical Physics 53: 12230.
Hofer-Szabó, G., and P. Vecsernyés. 2013a, submitted. Noncommutative common cause principles in algebraic quantum field theory. Journal of Mathematical Physics.
Hofer-Szabó, G., and P. Vecsernyés. 2013b, submitted. Bell inequality and common causal explanation in algebraic quantum field theory. Studies in History and Philosophy of Modern Physics.
Müller, V.F., and P. Vecsernyés. The phase structure of G-spin models, to be published.
Nill, F., and K. Szlachányi. 1997. Quantum chains of hopf algebras with quantum double cosymmetry. Communications in Mathematical Physics 187: 159–200.
Rédei, M. 1997. Reichenbach’s common cause principle and quantum field theory. Foundations of Physics 27: 1309–1321.
Rédei, M. 1998. Quantum logic in algebraic approach. Dordrecht: Kluwer.
Rédei, M., and J.S. Summers. 2002. Local primitive causality and the common cause principle in quantum field theory. Foundations of Physics 32: 335–355.
Rédei, M. and J.S. Summers. 2007. Remarks on causality in relativistic quantum field theory. International Journal of Theoretical Physics 46: 2053–2062.
Reichenbach, H. 1956. The direction of time. Los Angeles: University of California Press.
Summers, J.S. 1990. On the independence of local algebras in quantum field theory. Reviews in Mathematical Physics 2: 201–247.
Summers, J.S., and R. Werner. 1987a. Bell’s inequalities and quantum field theory, I: General setting. Journal of Mathematical Physics 28: 2440–2447.
Summers, J.S., and R. Werner. 1987b. Bell’s inequalities and quantum field theory, II: Bell’s inequalities are maximally violated in the vacuum. Journal of Mathematical Physics 28: 2448–2456.
Summers, J.S., and R. Werner. 1988. Maximal violation of Bell’s inequalities for algebras of observables in tangent spacetime regions. Annales de l’Institut Henri Poincaré – Physique Théorique 49: 215–243.
Szlachányi, K., and P. Vecsernyés. 1993. Quantum Symmetry and Braid Group statistics in G-spin models. Communications in Mathematical Physics 156: 127–168.
Wald, R.M. 1992. Correlations beyond the Horizon. General Relativity and Gravitation 24: 1111–1116.
Acknowledgements
This work has been supported by the Hungarian Scientific Research Fund OTKA K-100715.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Hofer-Szabó, G. (2014). Noncommutative Causality in Algebraic Quantum Field Theory. In: Galavotti, M., Dieks, D., Gonzalez, W., Hartmann, S., Uebel, T., Weber, M. (eds) New Directions in the Philosophy of Science. The Philosophy of Science in a European Perspective, vol 5. Springer, Cham. https://doi.org/10.1007/978-3-319-04382-1_38
Download citation
DOI: https://doi.org/10.1007/978-3-319-04382-1_38
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-04381-4
Online ISBN: 978-3-319-04382-1
eBook Packages: Humanities, Social Sciences and LawPhilosophy and Religion (R0)