SAHN Clustering in Arbitrary Metric Spaces Using Heuristic Nearest Neighbor Search

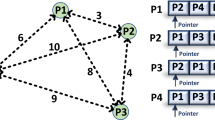
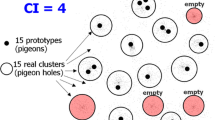
Abstract

Sequential agglomerative hierarchical non-overlapping (SAHN) clustering techniques belong to the classical clustering methods that are applied heavily in many application domains, e.g., in cheminformatics. Asymptotically optimal SAHN clustering algorithms are known for arbitrary dissimilarity measures, but their quadratic time and space complexity even in the best case still limits the applicability to small data sets. We present a new pivot based heuristic SAHN clustering algorithm exploiting the properties of metric distance measures in order to obtain a best case running time of $\mathcal{O}(n\log n)$ for the input size n. Our approach requires only linear space and supports median and centroid linkage. It is especially suitable for expensive distance measures, as it needs only a linear number of exact distance computations. In extensive experimental evaluations on real-world and synthetic data sets, we compare our approach to exact state-of-the-art SAHN algorithms in terms of quality and running time. The evaluations show a subquadratic running time in practice and a very low memory footprint.