Abstract
Many social, biological, and technological networks display substantial non-trivial topological features. One well-known and much studied feature of such networks is the scale-free power-law distribution of nodes’ degrees.
Several works further suggest models for generating complex networks which comply with one or more of these topological features. For example, the known Barabasi-Albert ”preferential attachment” model tells us how to create scale-free networks.
Since the main focus of these generative models is in capturing one or more of the static topological features of complex networks, they are very limited in capturing the temporal dynamic properties of the networks’ evolvement. Therefore, when studying real-world networks, the following question arises: what is the mechanism that governs changes in the network over time?
In order to shed some light on this topic, we study two years of data that we received from eToro: the world’s largest social financial trading company.
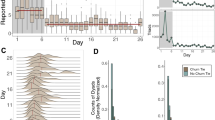
We discover three key findings. First, we demonstrate how the network topology may change significantly along time. More specifically, we illustrate how popular nodes may become extremely less popular, and emerging new nodes may become extremely popular, in a very short time. Then, we show that although the network may change significantly over time, the degrees of its nodes obey the power-law model at any given time. Finally, we observe that the magnitude of change between consecutive states of the network also presents a power-law effect.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Barabási, A.L., Albert, R.: Emergence of scaling in random networks. Science 286(5439), 509–512 (1999)
Watts, D.J., Strogatz, S.H.: Collective dynamics of ‘small-world’ networks. Nature 393(6684), 440–442 (1998)
Amaral, L.A.N., Scala, A., Barthélémy, M., Stanley, H.E.: Classes of small-world networks. Proceedings of the National Academy of Sciences 97(21), 11149–11152 (2000)
Newman, M.E.: Assortative mixing in networks. Physical Review Letters 89(20), 208701 (2002)
Girvan, M., Newman, M.E.: Community structure in social and biological networks. Proceedings of the National Academy of Sciences 99(12), 7821–7826 (2002)
Ravasz, E., Barabási, A.L.: Hierarchical organization in complex networks. Physical Review E 67(2), 026112 (2003)
Garlaschelli, D., Loffredo, M.I.: Patterns of link reciprocity in directed networks. Physical Review Letters 93(26), 268701 (2004)
Milo, R., Itzkovitz, S., Kashtan, N., Levitt, R., Shen-Orr, S., Ayzenshtat, I., Sheffer, M., Alon, U.: Superfamilies of evolved and designed networks. Science 303(5663), 1538–1542 (2004)
Dorogovtsev, S.N., Mendes, J.F.F.: Scaling behaviour of developing and decaying networks. EPL (Europhysics Letters) 52(1), 33 (2000)
Albert, R., Barabási, A.L.: Topology of evolving networks: local events and universality. Physical Review Letters 85(24), 5234 (2000)
Berger-Wolf, T.Y., Saia, J.: A framework for analysis of dynamic social networks. In: Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 523–528. ACM (2006)
Carley, K.M.: Dynamic network analysis. In: Dynamic Social Network Modeling and Analysis: Workshop Summary and Papers, Comittee on Human Factors, National Research Council, pp. 133–145 (2003)
Chin, A., Chignell, M., Wang, H.: Tracking cohesive subgroups over time in inferred social networks. New Review of Hypermedia and Multimedia 16(1-2), 113–139 (2010)
Kossinets, G., Watts, D.J.: Empirical analysis of an evolving social network. Science 311(5757), 88–90 (2006)
Palla, G., Barabási, A.L., Vicsek, T.: Quantifying social group evolution. Nature 446(7136), 664–667 (2007)
Skyrms, B., Pemantle, R.: A dynamic model of social network formation. In: Adaptive Networks, pp. 231–251. Springer (2009)
Anghel, M., Toroczkai, Z., Bassler, K.E., Korniss, G.: Competition-driven network dynamics: Emergence of a scale-free leadership structure and collective efficiency. Physical Review Letters 92(5), 58701 (2004)
Clauset, A., Shalizi, C.R., Newman, M.E.: Power-law distributions in empirical data. SIAM Review 51(4), 661–703 (2009)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer International Publishing Switzerland
About this paper
Cite this paper
Shmueli, E., Altshuler, Y., Pentland, A.”. (2014). Temporal Dynamics of Scale-Free Networks. In: Kennedy, W.G., Agarwal, N., Yang, S.J. (eds) Social Computing, Behavioral-Cultural Modeling and Prediction. SBP 2014. Lecture Notes in Computer Science, vol 8393. Springer, Cham. https://doi.org/10.1007/978-3-319-05579-4_44
Download citation
DOI: https://doi.org/10.1007/978-3-319-05579-4_44
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-05578-7
Online ISBN: 978-3-319-05579-4
eBook Packages: Computer ScienceComputer Science (R0)