Abstract
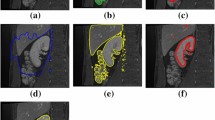
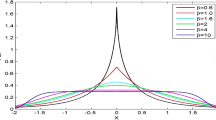
Active contour methods (ACM) are model-based approaches for image segmentation and were developed in the late 1980s. ACM can be divided into two classes: parametric active contour model and geometric active contour model. Geometric method is intrinsic model. Because of its completeness in mathematics, geometric active contour model overcomes many difficulties of the parametric active contour model. However, in medical images with heavy structural noise, the evolution of the geometric active contour will be seriously affected. To handle this problem, this paper proposed a multiscale geometric active contour model, based on the multiscale analysis method—bidimensional empirical mode decomposition. In the human kidney MR images, the proposed multiscale geometric active contour model successfully extracts the complex kidney contour.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Kass, M., Witkin, A., Terzopoulos, D.: Snakes: active contour models. Int. J. Comput. Vis. 1(4), 321–331 (1987)
Caselles, V., Catte, F., Coll, T., Dibos, F.: A geometric model for active contours in image processing. Number. Math. 66, 1–31 (1993)
Malladi, R., Sethian, J.A., Vemuri, B.C.: Shape modeling with front propogation: a level set approach. IEEE Trans. Patt. Anal. Mach. Intell. 17, 158–175 (1995)
Li, C., Kao, C.-Y., Gore, J.C., Ding, Z.: Implicit Active Contours Driven by Local Binary Fitting. In: Proceedings of the 2007 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (2007)
Li, C., Kao, C.-Y., Gore, J.C., Ding, Z.: Minization of Region-Scalable Fitting Energy for Image Segmentation. IEEE Transactions on Image Processing 10(10) (October 2008)
Li, C., Xu, C., Gui, C., Fox, M.D.: Level Set Evolution without Re-initialization: A new Variational Formulation. In: Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (2005)
Chan, T.F., Vese, L.A.: Active Contours without Edges. IEEE Transactions on Image Proceesing 10(2) (Febrauary 2001)
Huang, N., et al.: The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis. In: Proc. R. Soc. Lond. A, vol. 454, pp. 903–995 (1998)
Flandrin, P., Rilling, G.: Empirical mode decomposition as a filter bank. IEEE Signal Proc. Lett. 11(2), 112–114 (2004)
Cheng, J.S., Yu, D.J., Yang, Y.: Research on the intrinsic mode function(IMF) criterion in EMD method. Mech. Syst. Signal Proc. 20(4), 817–824 (2006)
Yushan, Z., et al.: Processing boundary effect of EMD based on AR model. Prog. Nat. Sci. 13(10), 1054–1059 (2003)
Nunes, J.C., Guyot, S., Delechelle, E.: Texture analysis based on local analysis of The bi-dimensional empirical mode decomposition. Mach. Vision Appl. 16, 177–188 (2005)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer International Publishing Switzerland
About this paper
Cite this paper
Li, L., Gu, J., Wen, T., Qin, W., Xiao, H., Yu, J. (2014). Multiscale Geometric Active Contour Model and Boundary Extraction in Kidney MR Images. In: Zhang, Y., Yao, G., He, J., Wang, L., Smalheiser, N.R., Yin, X. (eds) Health Information Science. HIS 2014. Lecture Notes in Computer Science, vol 8423. Springer, Cham. https://doi.org/10.1007/978-3-319-06269-3_23
Download citation
DOI: https://doi.org/10.1007/978-3-319-06269-3_23
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-06268-6
Online ISBN: 978-3-319-06269-3
eBook Packages: Computer ScienceComputer Science (R0)